Лекция 3. Функция полезности
Определение функции полезности.
Свойства функции полезности.
Товары заменители и предельные нормы замещения.
Определение функции полезности.
Система
предпочтений индивида указывает, какой
из двух наборов предпочтительнее для
него. Система предпочтений непрерывна,
если для любого
множество предпочтительности
и множество непредпочтительности
замкнуты (рис.1).
В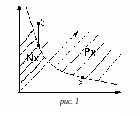
о
многих случаях желательно и удобно
оценивать привлекательность набора
товара количественно, т.е. приписать
каждому набору
какое-то число
,
тем самым получить функцию
.
Главные требования к этой функции – это чтобы она отражала отношения слабого предпочтения, т.е. чтобы она удовлетворяла следующим условиям:
,
если
;
,
если
;
,
если
.
Вот такую функцию и называют функция полезности.
Функция полезности является постоянной на каждом классе безразличия, так что ее наглядно можно представить себе, как функцию, которая пересчитывает классы безразличия в сторону все большего предпочтения наборов товаров.
С функцией гораздо удобнее работать, чем с системой предпочтений. При этом необходимо сформировать условия, при котором функция полезности существует. Это условие названо теоремой Дебре.
Теорема Дебре: если система предпочтений непрерывна, то существует непрерывная функция полезности.
Надо
отметить, что функция полезности, если
она существует, не определяется
единственным образом. Главное требование
к функции полезности – она должна
отражать систему предпочтений.
Поэтому если
– функция полезности, то
(
),
где
– произвольная, строго возрастающая
числовая функция на R, тоже является ФП.
То есть из этого можно сделать вывод:
функция полезности не является какой-то
уникальной, а этих функций огромное
множество.
Свойства функции полезности.
Функция полезности является неубываемой, то есть если , то , а если , то тем более .
Будем полагать, что функция полезности дифференцируемая, тогда частная производная
,
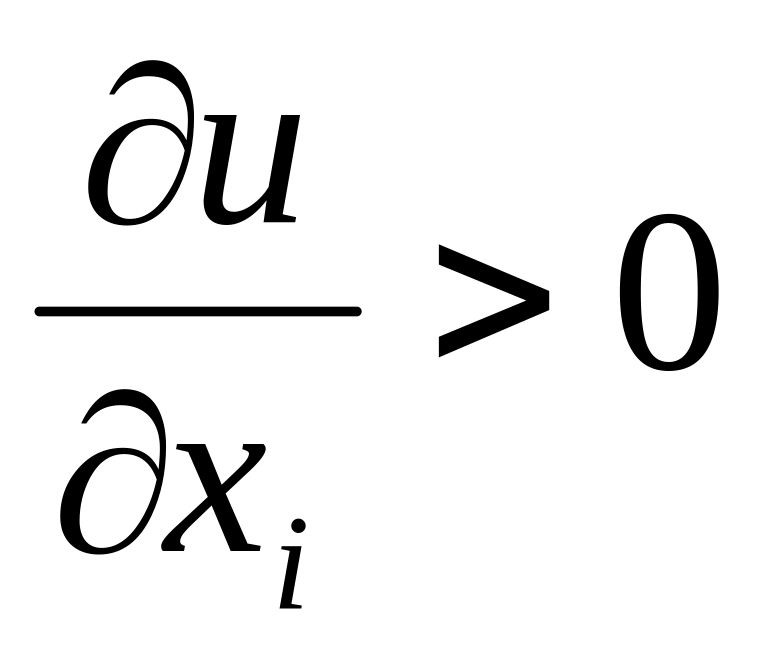называется предельной полезностью
каждого товара. Она положительна и это
означает, что если даже потребитель
имеет набор товаров
,
всё равно он желает еще приобрести i-й
товар. Возрастание потребления товара
при постоянном потреблении другого
ведет к повышению потребительской
оценки. Вектор, составленный из частных
производных
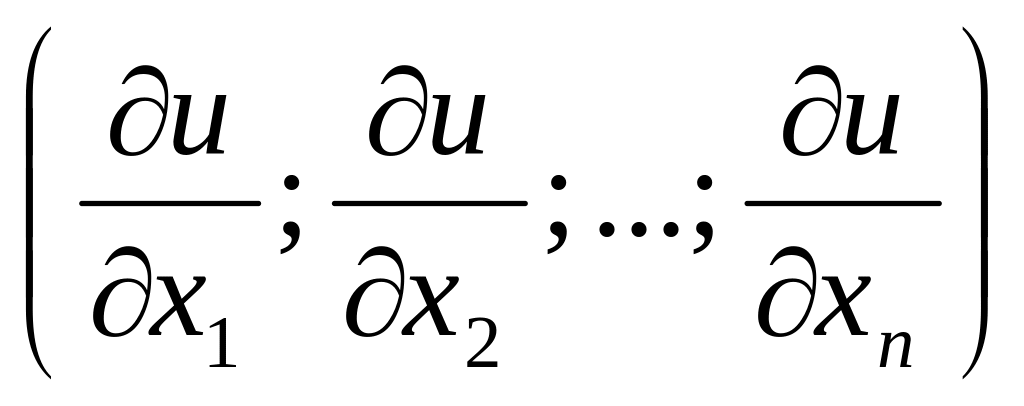называется вектором
предельных полезностей
или градиентом
,
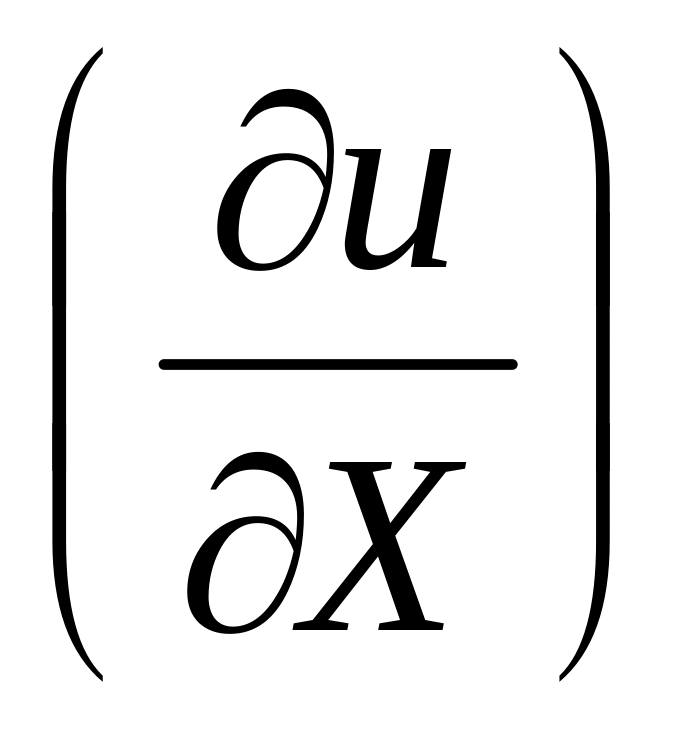который показывает направление
наибольшего роста функции.Функция полезности должна быть дважды дифференцируемой и матрица Гёссе, состоящая из вторых частных производных, должна быть отрицательной.
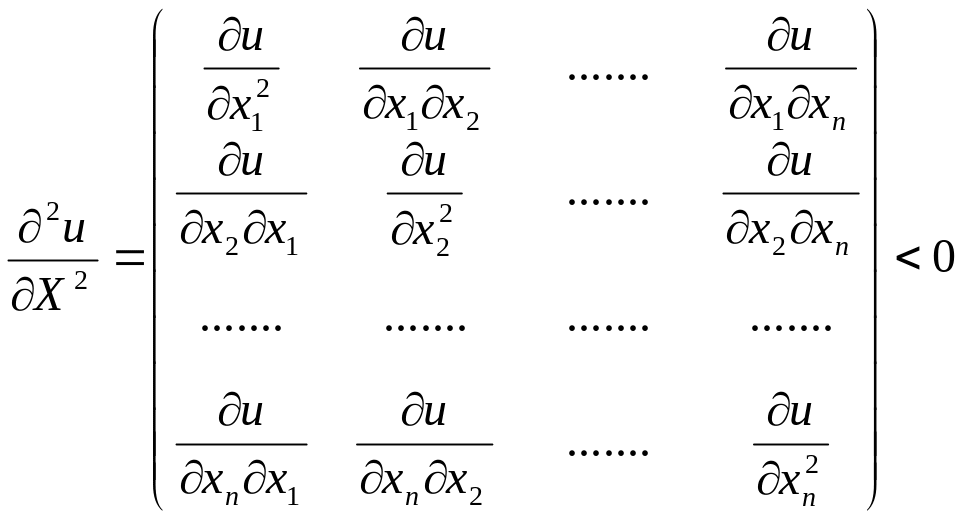
Из
отрицательности матрицы Гёссе следует,
что
для любого
,
т.е. предельная полезность любого
товара уменьшается по мере увеличения
его потребления. Это называется законом
предельной полезности
или первым
законом Гёссе.
Аксиоматический подход к построению функций полезности обладает крупным недостатком, связанным с трудностью проверки выше приведенных свойств в реальных условиях. Поэтому в экономике исследуют конкретные виды функции полезности, причем нужная функция подбирается из необходимости соответствия реальным данным.
Виды функций полезности:
Неоклассическая функция:
,
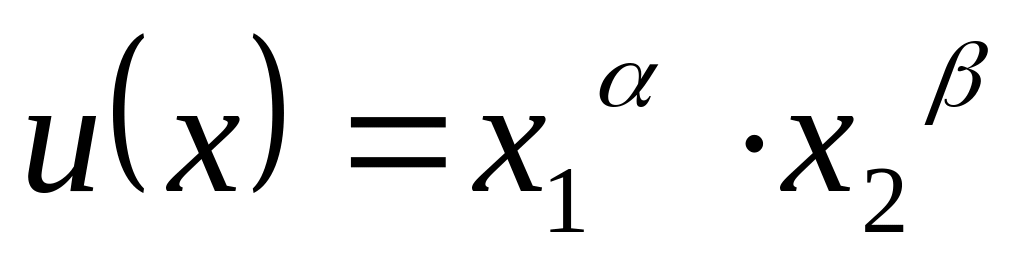где
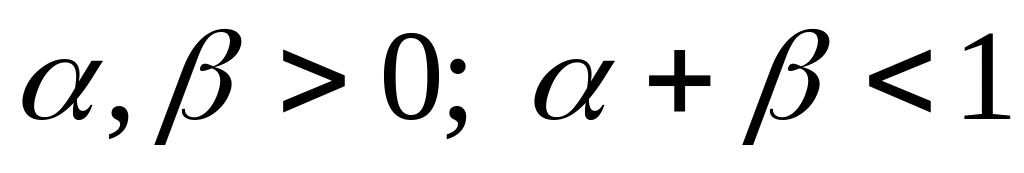.Линейная функция:
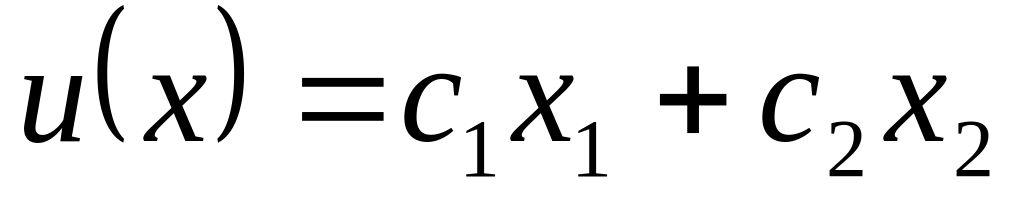.Квадратическая функция:
,
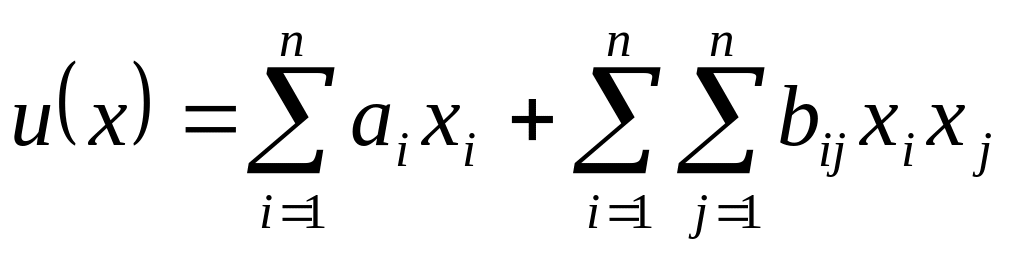где
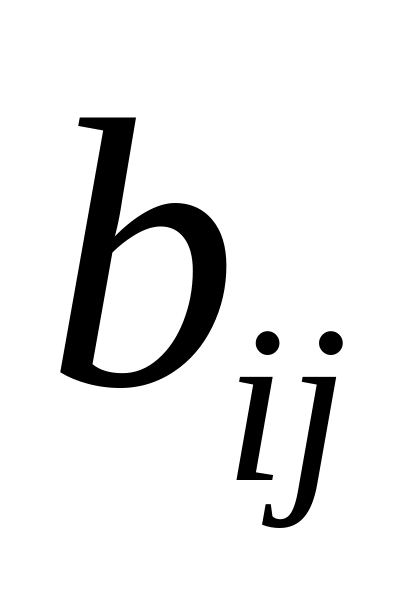– матрица, причем эта матрица отрицательно
определена и
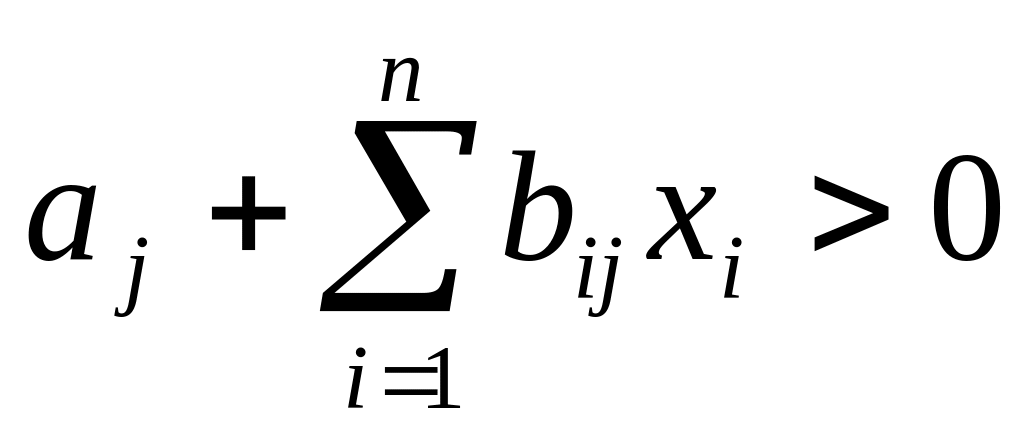для
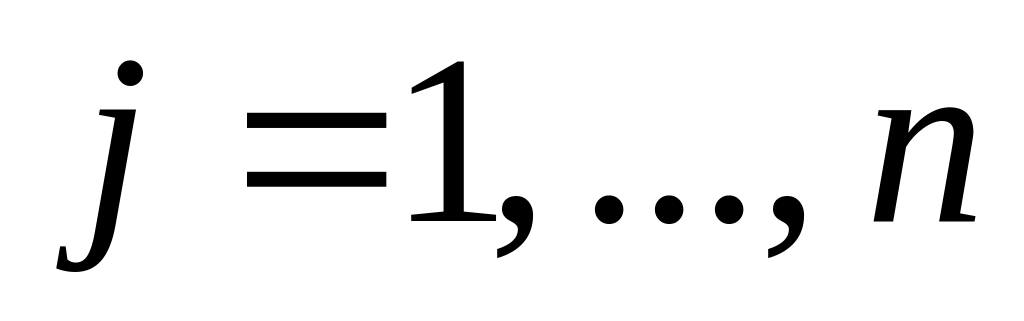.Логарифмическая функция:
,
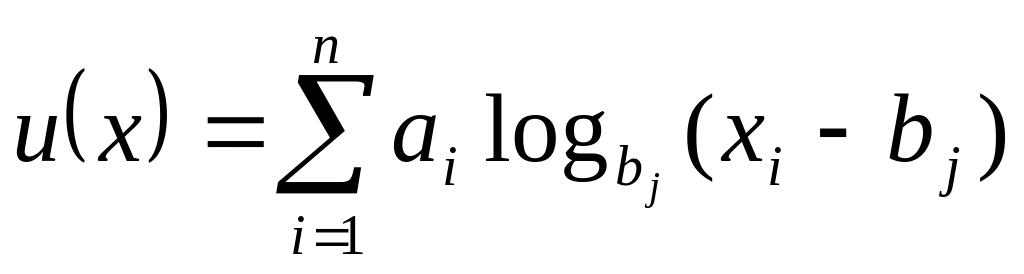где
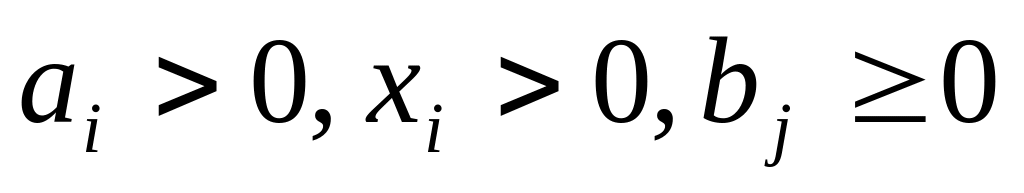для
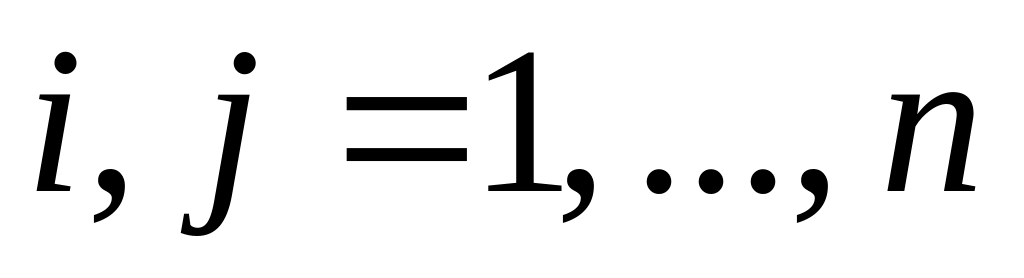(основание логарифма
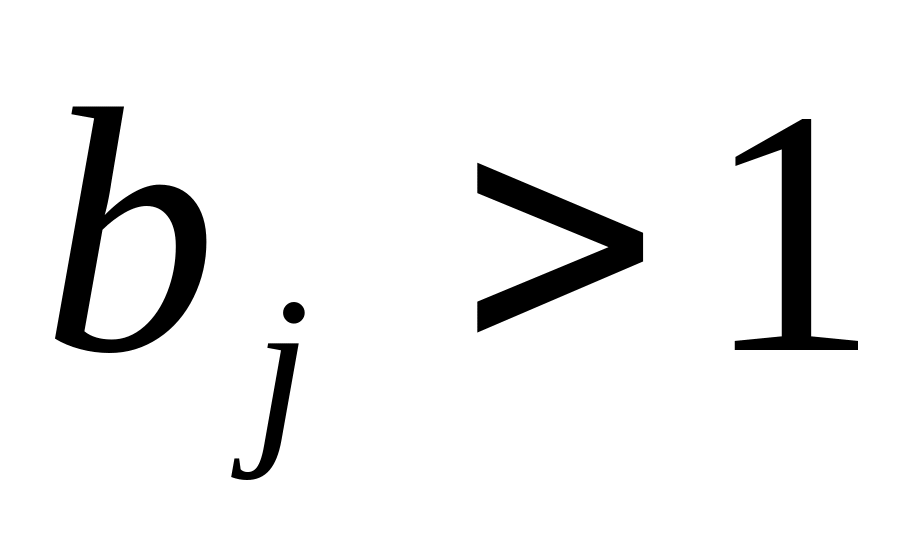).Пропорциональность (только крайний её случай):
,
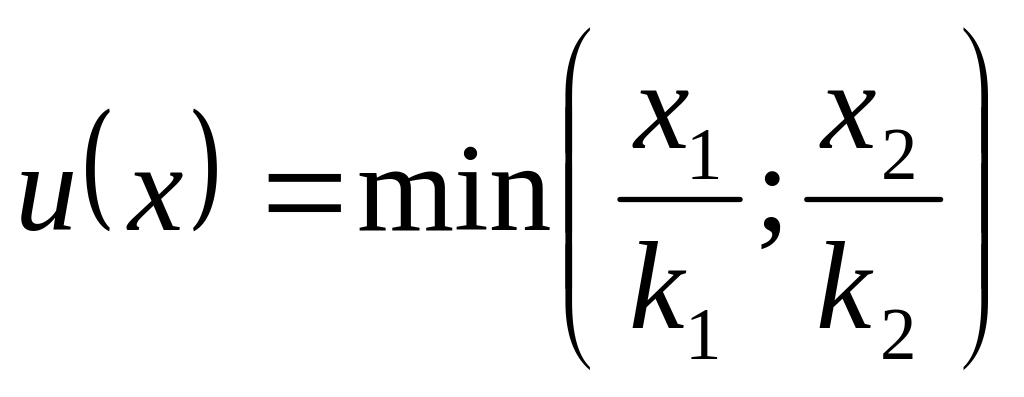где
.
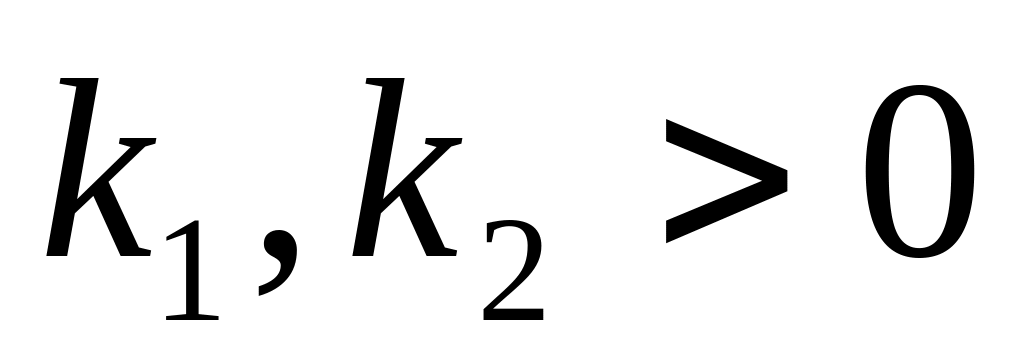