2. Бюджетное множество.

Пусть вектор – это вектор цен. Зафиксируем какую-нибудь денежную сумму – доход.

Множество наборов товаров стоимостью при ценах называют границей этого бюджет­ного множества ( ).

Бюджетное множество и его граница зависят от цен и доходов так, что их точнее можно обо­значать таким образом: , .

Бюджетное множество и его границу можно представить в виде обычных неравенств и ра­венств:

Все это можно также представить в виде векторных неравенств и равенств:

Пример 1.

Рассмотрим бюджетное множество для случая двух товаров (рис 1).

П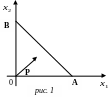 ри и бюджетное множество – это треугольник AOB.

Точка А имеет координату , точка В – .

Отрезок АВ – граница бюджетного множества , он перпендику­лярен вектору цен . Если доход возрастает, граница бюджет­ного множества будет двигаться в направлении вектора цен. При из­менении цен об изменении бюджетного множества можно будет су­дить по перемещению т. А и т. В.

Бюджетное множество выпукло, ограничено и замкнуто.

Выпуклость:

Пусть , , тогда если и при этом , то можно рассмот­реть такую линейную комбинацию: . Отсюда следует, что , значит .

Ограниченность:

Пусть , тогда если , то для . Это и доказывает ограниченность, т.е. множество ограниченно.

Замкнутость:

Пусть для любого и . Тогда в силу непрерывности линейной функ­ции и поскольку , то и , т.е. .

3. Индивид-потребитель и система его предпочтений.

Проблема рационального поведения потребителя заключается в решении вопроса о том, какие количества товаров или услуг он может приобрести при заданных целях и при данном доходе.

Мы будем придерживаться ранее сформулированной аксиомы потребителя. Выбор потребите­лем некоторого набора товаров во многом зависит от его вкусов и желаний. Потребитель разли­чает набор товаров, предпочитая один набор товаров другому.

Запись означает, что потребитель предпочитает набор набору или он не делает ме­жду ними различия. Отношения такого вида называют слабым предпочтением. Оно формирует еще два отношения:

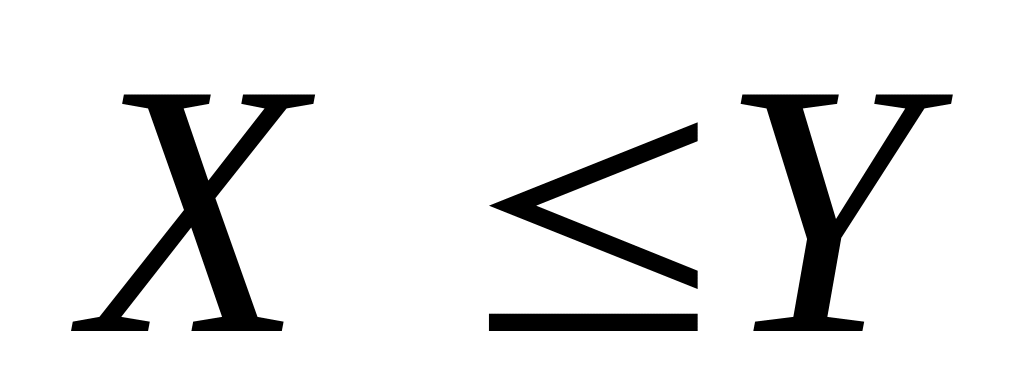• называется отношением равноценности или безразличия. Оно выполняется тогда и только тогда, если и .

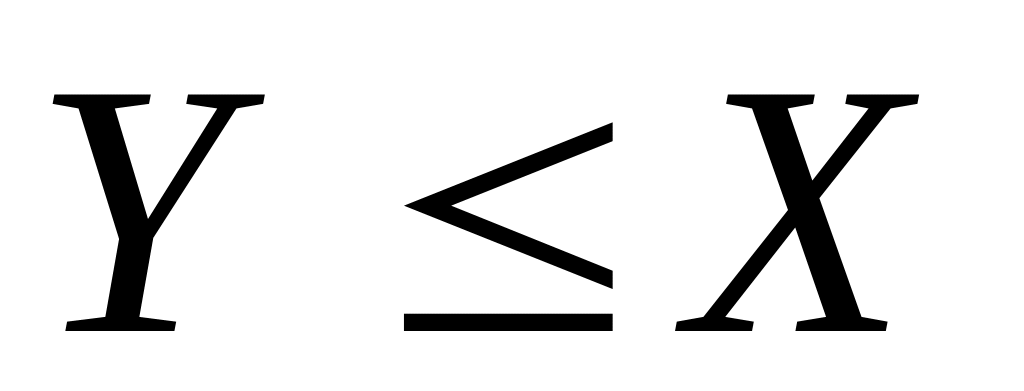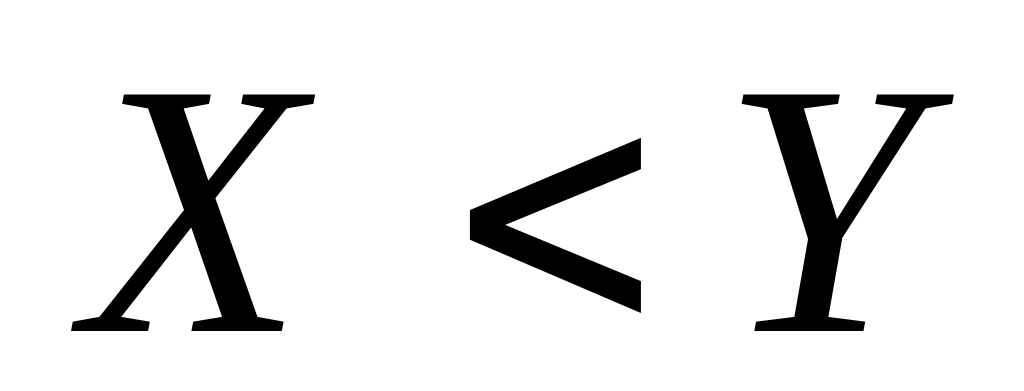• – отношение строгого предпочтения.

Свойства отношений:

• Рефлективность – если ;

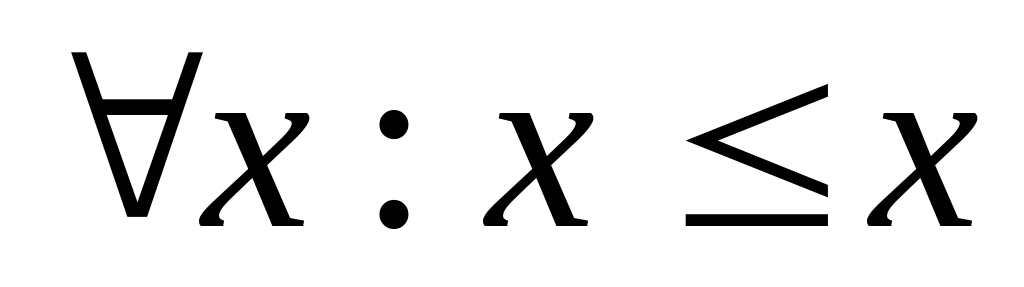• Симметричность – ;

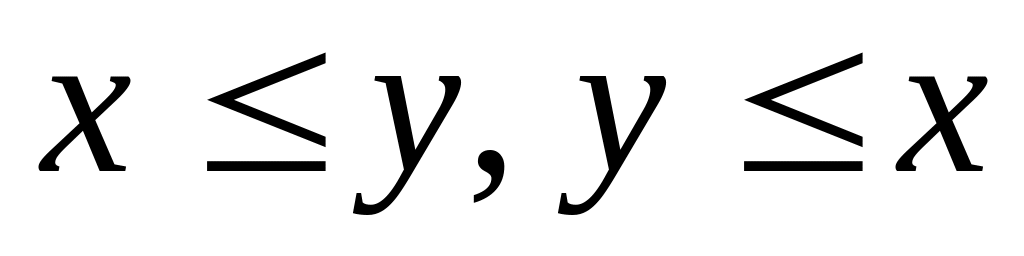• Транзитивность – .

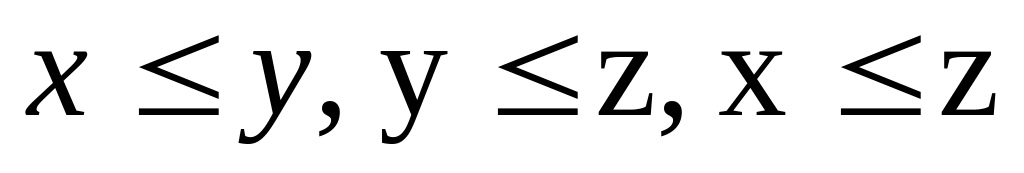Аксиомы системы преимуществ:

1. Отношение слабого предпочтения рефлексивно, транзитивно и совершенно.

2. Отношение безразличия рефлексивно, симметрично, совершенно.

3. Отношение строгого предпочтения транзитивно.

4. Для любого набора товаров 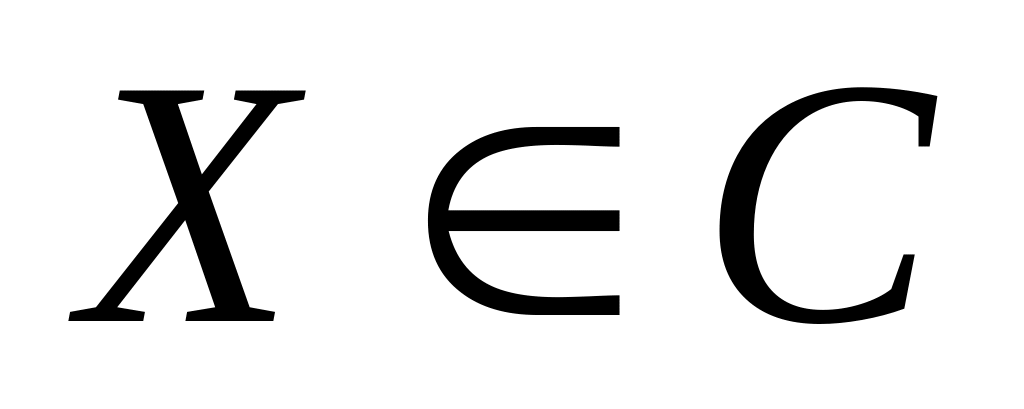множество предпочтительности 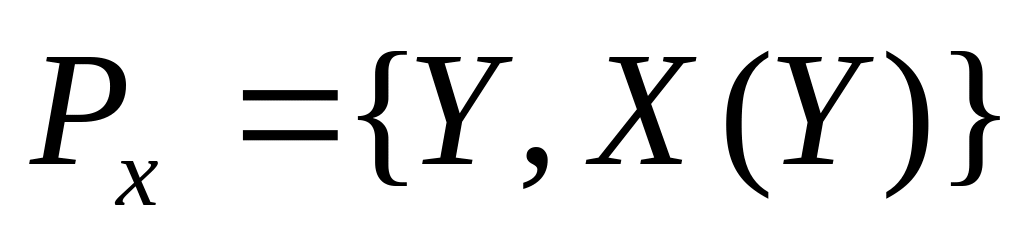выпукло.

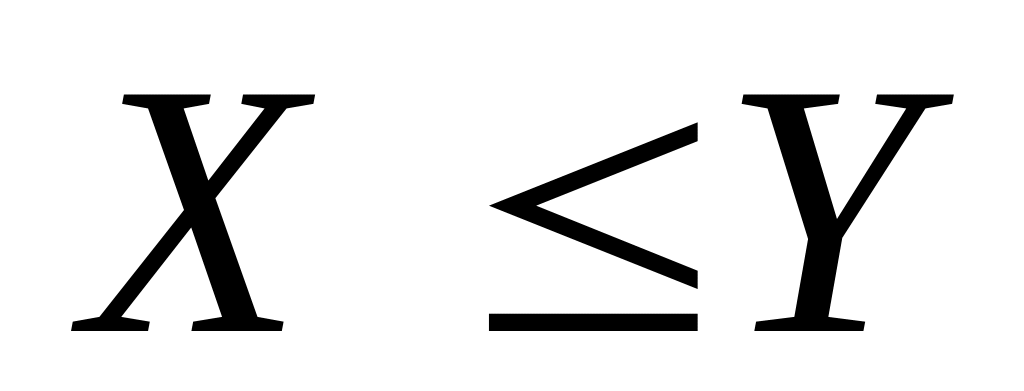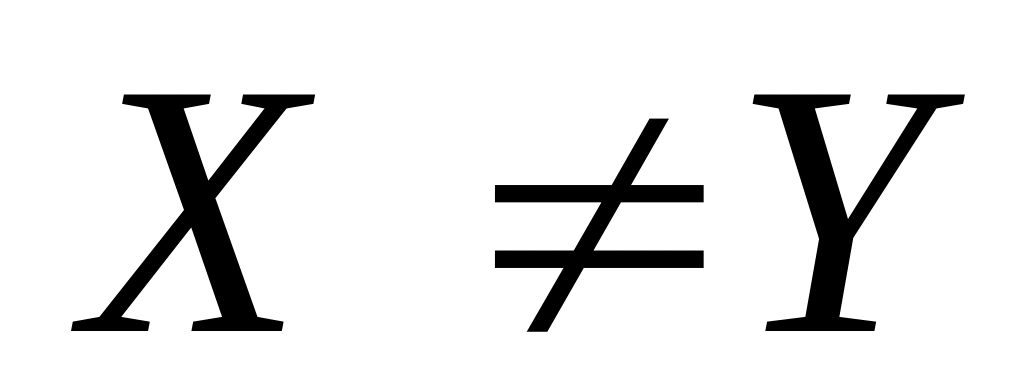5. Каждый товар желателен для индивида, если , то и , а если к тому же (т.е. 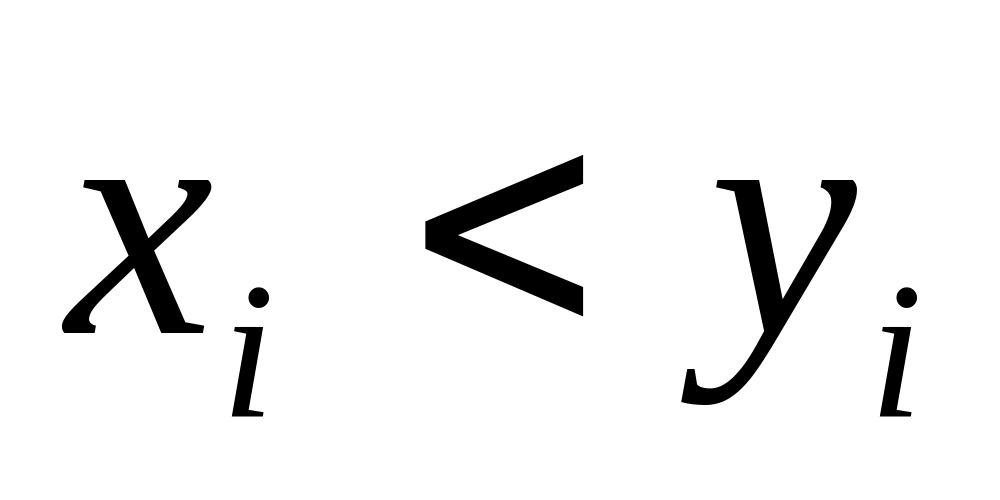для некоторого i), то .

Совершенность означает, что индивид в состоянии сравнить по привлекательности любые два товара.

Рефлективность означает, что любой набор товаров равноценен сам себе.

Выпуклость означает, что лучше иметь комбинацию товаров пусть даже и в меньших количест­вах, чем один какой-то товар.

Рассмотрим пример системы предпочтительности, которая будет не транзитивна.

Свойства
Дача	Цена	Размер	Удобства		Л – лучшая
A	Л	Х	С		С – средняя
B	С	Л	Х		Х – худшая
C	Х	С	Л		A<B; B<C; A<C

На этом примере видна важность отношения транзитивности для отношения предпочтения.

Если условия транзитивности не выполняются, то мы получаем своеобразный замкнутый про­цесс, который еще называют денежный насос.

Отношение равноценности (безразличия) рефлексивно, симметрично, транзитивно. Любое от­ношение, которое обладает такими свойствами, называют эквивалентностью.

Любая эквивалентность на множестве разбивает это множество на поперечные множества, ко­торые называют классами эквивалентности.

Каждый набор и пространство товаров попадает в один из классов безразличия, в тот, где соб­раны наборы одинаково ценные с ними (для индивида).

Рассмотрим типичную картину для двух видов товаров.

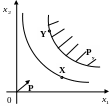– классы безразличия наборов X и Y;

– направление предпочтения;

– множество предпочтительности Y.