3. Основные типы моделей.

Математические модели подразделяются на классы по ряду признаков, относящихся к особен­ностям моделируемого объекта, цели моделирования или использоваемого инструментария.

Модели классифицируются по следующим признакам:

1. По общему целевому предназначению:

• Теоретические – модели позволяющие изучать общие свойства экономики и её характер­ных элементов;

• Прикладные – дают возможность оценить параметры функционирования конкретного эконо­мического объекта, сформулировать рекомендации для принятия практического решения.

2. По степени агрегирования модели:

• Макроэкономические – модели описывающие экономику, как единое целое, связывая меж­ду собой укрупнённые материальные и финансовые показатели, такие как потребление, инве­стиции, количество денег, занятость и процентная ставка;

• Микроэкономические – описывают взаимодействие структурных и функциональных со­ставляющих экономики, либо поведение такой составляющей в рыночной среде; бывают от­крытые и закрытые.

3. По конкретному целевому предназначению:

• Балансовые – отображают соответствие наличия ресурсов их использованию;

• Равновесные – они описывают такие состояния в экономике, когда результат всех сил стре­мящихся вывести её из данного состояния равен нулю;

• Трендовые – отображают развитие системы, через какую либо тенденцию;

• Оптимизационные – модели, изучающие максимальные полезности потребителей или при­были фирмы;

• Имитационные – модели, которые используются в процессе машинной имитации экономи­ческих процессов.

4. По размерности:

   • Маломерные;

   • Многомерные.

5. В зависимости от показателя времени:

• Статические – в них описывается состояние объекта в конкретный момент или период вре­мени;

• Динамические – включают взаимосвязи переменных во времени.

6. С учётом показателя неопределённости:

• Детерминированные – используют жёсткие функциональные связи;

• Стохастические – модели, в которых существует показатель случайности.

7. По характеристике математических объектов:

• Матричные – «Модель межотраслевого баланса»;

• Линейные – «Кейнсианская функция потребления»;

• Нелинейные – «Производственная функция Кобба-Дугласа»;

• Корреляционно-регрессивные;

• Модели теории игр;

• Модели сеточного планирования.

Лекция 2. Индивид-потребитель и система его предпочтений

1. Пространство товаров и цена.

2. Бюджетное множество.

3. Индивид-потребитель и система его предпочтений.

1. Пространство товаров и цена.

Под товаром понимаются некоторые блага или услуги, поступившие в продажу в определенное время и в определенном месте.

Будем считать, что имеется видов товаров. Количество i-го товара обозначается , тогда не­который набор товаров обозначается таким образом: . Так как упорядоченный набор из чисел – это вектор, то является n-мерным вектором. Вообще, набор товаров – это вектор столбец: .

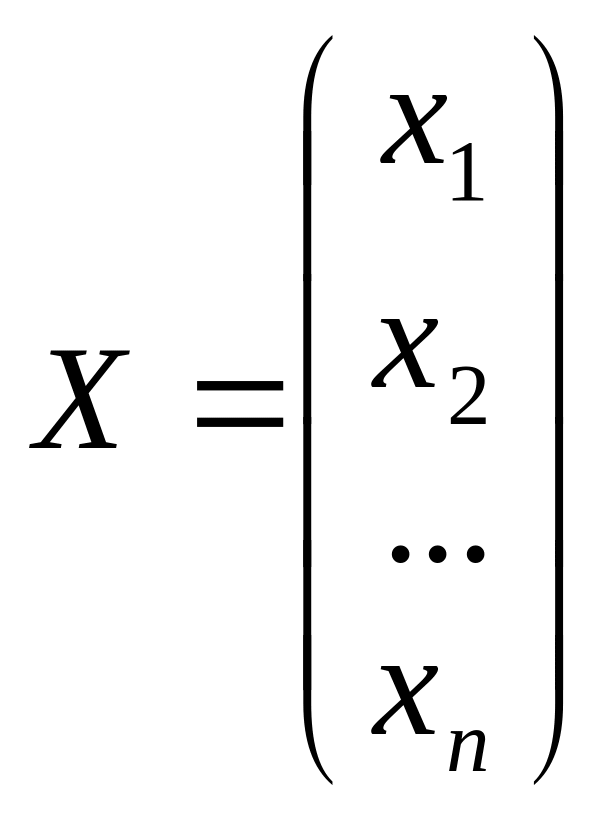Будем рассматривать только не отрицательное количество товаров, то есть каждое или .

Множество всех наборов товаров называют пространством товаров ( ). Это множество назы­вают пространством, так как в нем можно сложить любые наборы и умножить их на неотри­цательное число. Возможность умножения любого набора товаров на любое неотрицательное число отражает предположение о безграничной делимости и умножении товаров (любой товар представляется в виде сахарного песка). Набор товаров можно трактовать, как корзину, в которой лежат эти товары в соответственном количестве.

Пространство товаров представляет собой часть арифметического линейного пространства . Его еще называют неотрицательным октаном.

Поэтому при работе с пространством товаров можно использовать структуру линейного про­странства.

Так как для любого подмножество называют лучом, проходящим через , а множество называют отрезком, который соединяет точки и . Подмножество является выпускным, если вместе с любыми и , которые принадле­жат весь соединяющий их отрезок лежит в .

Предполагается, что каждый товар имеет цену. Цена строго положительна. Цена i-го товара – , тогда – вектор-строка цен.

Для набора товаров и вектора цен существует скалярное произведение, которое называют ценой набора: .