7.4 Изгиб при неравномерном нагреве

Рассмотрим действие на неравномерно нагретый стержень моментов M_X и M_Y относительно главных осей его поперечного сечения X и Y. Силовые напряжения будем определять по формуле (7.5) при β = 0:

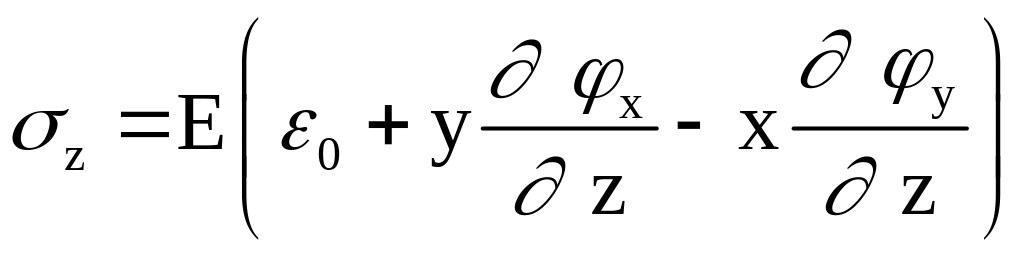. (7.19)

Используем условия равновесия отсеченной (правой) части стержня в отсутствии растягивающей силы (см. Рисунок 7.1):

Подстановкой σ_z из формулы (7.19) образуем систему уравнений:

(7.20)

Используя свойства главных (центральных) осей , , , определим параметры деформации:

, (7.21)

что дает возможность определять напряжения исходя из формулы (7.19):

. (7.22)

Если значение модуля упругости постоянно E(x, y)=E=const, то напряжение линейно зависит от координат и не зависит от модуля упругости:

. (7.23)

Такое значение напряжения будем называть изоупругим значением при изгибе. По сути, оно состоит из напряжения , связанного с действием момента М_Х, определяющего распределение напряжений вдоль оси Y , и напряжения , связанного с действием момента М_Y, определяющего распределение напряжений вдоль оси X.

Если ввести средние осевые значения модуля упругости

и , (7.24)

то распределение напряжений (7.23) заменится формулой

. (7.25)

Таким образом, при изгибе влияние зависимости модуля упругости от температуры можно учесть коррекцией слагаемых изоупругого значения (7.23) коэффициентами, равными отношению местного значения модуля упругости к соответствующему среднему осевому значению. В "горячих" частях сечения, как правило, и . Следовательно, напряжения будут меньше изоупругого значения (7.23). В "холодных" частях, наоборот, , и напряжения превышают изоупругое значение.

Рисунок 7.5 - Силовые напряжения при изгибе:

а — схема нагружения; б — примеры распределения температур;

в — эпюры напряжений

Эта закономерность распределения напряжений проиллюстрирована на Рисунок 7.5 для симметричного и линейного распределений температуры при изгибе относительно одной оси Х (М_Х >0, M_Y = 0).

Изоупругие значения, рассчитанные по формуле (7.23), можно использовать как первоначальную оценку напряжений на этапе предварительного расчета, когда распределение температуры еще неизвестно. С помощью формулы (7.25) они легко могут быть скорректированы по ожидаемым значениям отношений модулей упругости. После определения температурного поля можно провести окончательный расчет распределения напряжений по формуле (7.25), учтя также изменение положения главных осей (7.24) при неравномерном нагреве.

7.5 Температурные напряжения в неравномерно нагретом стержне

Определим напряжения, возникающие в ненагруженном стержне вследствие неравномерного прогрева его сечения, когда температура изменяется по координатам x и y и не изменяется по z (Рисунок 7.1).

Напряжение в произвольной точке сечения определяется по формуле (7.5):

. (7.26)

Параметры деформации определим из условий равновесия отсеченной (правой ) части стержня в отсутствии внешних нагрузок:

(7.27)

Подстановкой σ _z =σ (x, y) образуем систему уравнений:

(7.27)

Используя свойства главных центральных осей , , , найдем параметры деформации:

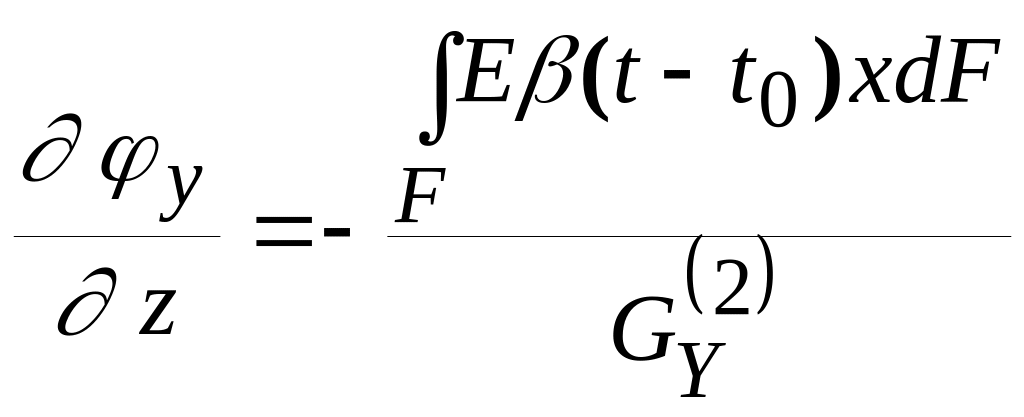, , . (7.28)

Зная их, определим распределение температурных напряжений (7.26):

(7.29)

.

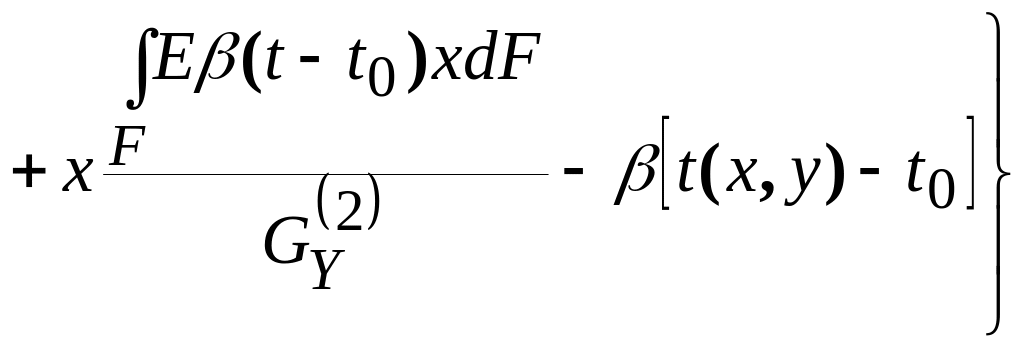В двигателестроительных конструкторских бюро России и Украины эта формула используется для расчетов температурных напряжений в лопатках турбин и известна как формула Биргера — Малинина.

Если температуры в сечении стержня таковы, что изменением модуля упругости и коэффициента теплового расширения можно пренебречь, то из нее следует более простая зависимость:

, (7.30)

где — средняя температура сечения.