
- •1 Влияние охлаждения деталей турбин на термодинамическое совершенство и ресурс
- •1.1 Общие тенденции развития двигателей
- •1.2 Обеспечение ресурса
- •1.3 Требования к системам охлаждения
- •1.4 Потери, связанные с охлаждением гтд
- •1.5 Термодинамический анализ
- •2 Анализ условий работы деталей осевых газовых турбин
- •2.1 Лопатки газовых турбин
- •2.1.1 Профиль проточной части и изменение параметров
- •2.1.2 Тепловое состояние лопаток
- •2.1.3 Нагрузки, действующие на лопатки
- •3.2 Эффективность охлаждения
- •3.3 Развитие систем охлаждения рабочих лопаток
- •3.3.1. Лопатки с внутренним конвективным охлаждением
- •3 Распределение температуры в сечении лопатки с пленочно-конвективным охлаждением .3.2 Лопатки с конвективно-заградительным охлаждением
- •3.3.3 Лопатки с пористым охлаждением
- •5 Задание граничных условий теплообмена на наружной и внутренней поверхности охлаждаемых лопаток
- •5.1 Изменение скорости и температуры в пограничном слое. «Греющая» и «охлаждающая» температура
- •5.2 Теплообмен в пограничном слое (конвективный теплообмен)
- •5.3 Теплообмен лопаток с газовым потоком
- •5.3.1 Определение температуры газа
- •5.3.1.2 Учет сегрегации потока в канале рабочего колеса
- •5.3.2 Особенности течения газа в решетках турбинных лопаток
- •5.3.2. Теплообмен между газом и поверхностью профиля лопатки
- •5.2 Теплообмен лопаток с охлаждающим воздухом
- •5.2.1 Гидравлический расчет системы подвода охлаждающего воздуха
- •5.2.2 Определение температуры охлаждающего воздуха на входе в расчетное сечение лопатки
- •5.2.3 Теплообмен в каналах охлаждения
- •5.3 Эффективность конвективного охлаждения
- •5.3.1 Методика определения эффективности охлаждения
- •5.3.2 Влияние подогрева воздуха в канале на эффективность конвективного охлаждения лопатки
- •6 Термические напряжения и их анализ
- •6.1 Термопрочностные явления в деталях
- •6.2 Температурные напряжения в изотермичном стесненном стержне
- •6.3 Температурные напряжения в неравномерно нагретом стержне с жесткой концевой пластиной (бандажом)
- •6.4 Температурные напряжения в стержне со свободным торцом
- •6.7 Малоцикловая термическая усталость
- •7 Особенности определения напряженно- деформированного состояния охлаждаемых лопаток
- •7.1 Гипотеза плоских сечений
- •7.2 Упругогеометрические характеристики сечения
- •7.3 Растяжение при неравномерном нагреве
- •7.4 Изгиб при неравномерном нагреве
- •7.5 Температурные напряжения в неравномерно нагретом стержне
- •7.6 Определение суммарных напряжений в сечении лопатки
- •8 Оптимизация системы охлаждения лопатки
6.3 Температурные напряжения в неравномерно нагретом стержне с жесткой концевой пластиной (бандажом)
Рассмотрим длинный стержень 1 прямоугольного сечения 2, размеры которого можно характеризовать соотношением L >> H >> h (Рисунок 6.2). На конце стержня имеется жесткая пластина-бандаж 3. Для простоты будем считать, что температура изменяется только по ширине стержня H, при этом профиль температуры симметричный и крайние волокна нагреты больше средних.
Д
Рисунок
6.2
- Распределение
температуры и температурных напряжений
в бандажированном стержне: пунктир —
свободные температурные перемещения
волокон; штрих пунктир — результирующее
положение бандажа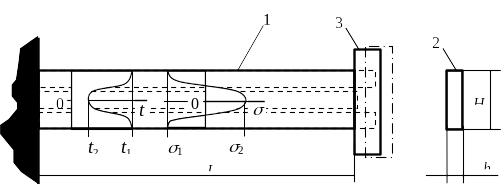
(6.2)
где σ1, σ2 — напряжения в крайних и среднем волокнах.
Условие равновесия пластины-бандажа есть равенство нулю суммы сил, действующих на нее со стороны горячих и холодных волокон:
(6.2)
где F1, F2 — площади сечений горячих и холодных волокон.
Рассматривая выражения (6.2) и (6.2) как систему трех уравнений с тремя неизвестными σ1, σ2и ε, получим
(6.2)
где tср=(2F1t1+ F2t2)(2F1+F2) — средняя температура сечения.
Из полученных выражений следует, что температурные напряжения в более нагретых волокнах, где t1> tср, будут напряжениями сжатия (σ1<0), в менее нагретых, где t2< tср,— напряжениями растяжения (σ2>0). Величина напряжений не зависит от начальной температуры детали, а определяется распределением температуры по сечению. Наблюдаемая деформация ε будет такой же, как при нагреве стержня до средней температуры.
6.4 Температурные напряжения в стержне со свободным торцом
И
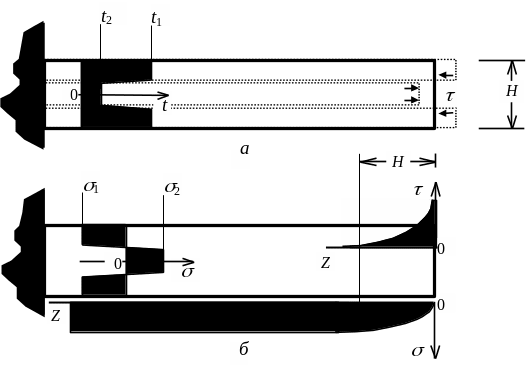 Рисунок
6.3 - Стержень со свободным торцом:
а
— распределение температуры и свободные
температурные перемещения волокон; б
— распределение температурных напряжений
Рисунок
6.3 - Стержень со свободным торцом:
а
— распределение температуры и свободные
температурные перемещения волокон; б
— распределение температурных напряжений
Примечание. Принцип Сен-Венана состоит в следующем. На удалении от участка поверхности, порядка наибольшего линейного размера участка, особенности распределения нагрузки в пределах этого участка несущественны, важна только величина равнодействующего усилия. В рассматриваемом случае равнодействующее усилие на торце стержня равно нулю, как и в предшествующем случае бандажированного стержня.
Принцип Сен-Венана указывает не точную величину расстояния, на котором не сказываются отличия в распределении нагрузок, а лишь порядок ее порядок.
6
Рисунок
6.5 – Изменение напряжений при
термоциклировании:
а
- схема испытаний; б
- изменение температуры; в
- изменение
напряжений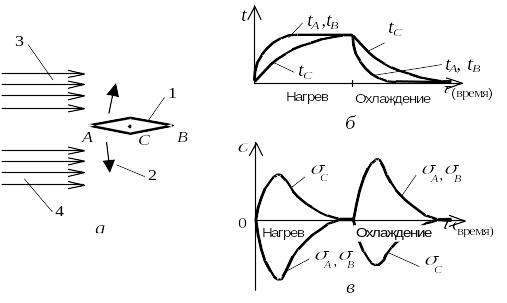
При нагреве деталей в газовом потоке или иным образом изменение температуры в разных точках детали происходит с разной скоростью. В детали возникают неравномерное температурное поле и, как следует из предшествующих примеров, температурные напряжения. При запуске и остановке двигателя в подобных условиях оказываются многие детали: жаровые трубы камер сгорания, сопловые и рабочие лопатки, диски и корпуса турбин, сопла и др. В технической литературе это явление иногда называют термоударом.
Для изучения поведения материалов в условиях термоудара на специальных установках проводят их испытания на кратковременную термическую прочность. Образец материала в виде стержня ромбовидного сечения 1 качалкой 2 вносится последовательно в газовый поток керосиновой горелки 3 и поток холодного воздуха 4 (Error: Reference source not found, а). В процессе нагрева острые передняя и задняя кромки (точки А и В) нагреваются быстрее, чем более массивная средняя часть сечения (точка С). В сечении образца на линии АСВ образуется симметричный профиль температуры. Разность температур по сечению в определенный момент времени достигает максимума, затем уменьшается (Error: Reference source not found, б). По истечении некоторого времени в образце устанавливается стационарный режим с равномерно прогретым сечением.
В образце возникают температурные напряжения сжатия в более нагретых передней и задней кромках и растяжения в средней части сечения. В момент максимума разности температур температурные напряжения имеют максимальные по модулю значения. На стационарном режиме температурные напряжения исчезают. При охлаждении в потоке холодного воздуха острые кромки остывают быстрее, чем середина образца, и в них возникают температурные напряжения растяжения, а в середине образца - сжатия (Error: Reference source not found, в).
Значительные температурные напряжения приводят к искривлению кромок и разрушению образца. Образцы из керамических материалов чаще разрушаются в процессе охлаждения, когда в кромках возникают значительные температурные напряжения растяжения. Это вызвано тем, что предел прочности при растяжении у таких материалов значительно меньше предела прочности при сжатии.
