2. Пример решения задачи №1 «Изучение колебаний динамической

Системы»

1. Свободные колебания

Исходная схема для анализа колебаний материальной точки М показана на рисунке 2.1.

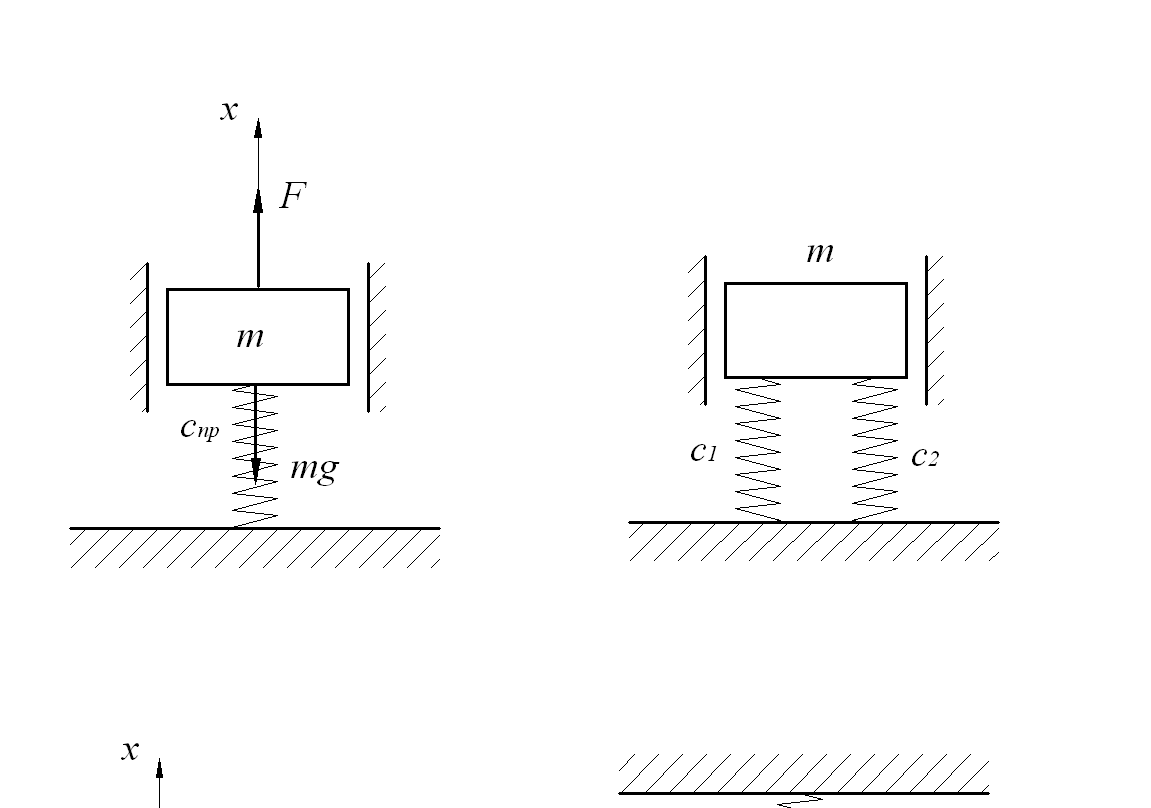
Рисунок 2.1 – Исходная схема динамической системы

Исходными данными для расчета являются:

масса материальной точки: m = 15 кг;

жесткость упругих элементов: с₁ = 0,55 Н/м, с₂ = 0,65 Н/м;

начальное перемещение (t=0): x₀ = 0,09 м;

начальная скорость (t=0): v₀ = 0,3 м/с.

Заменим два упругих элемента одним, имеющим приведенную жесткость с_пр. Для упругих элементов, соединенных параллельно, приведенная жесткость определяется по формуле:

(2.1)

Н/м

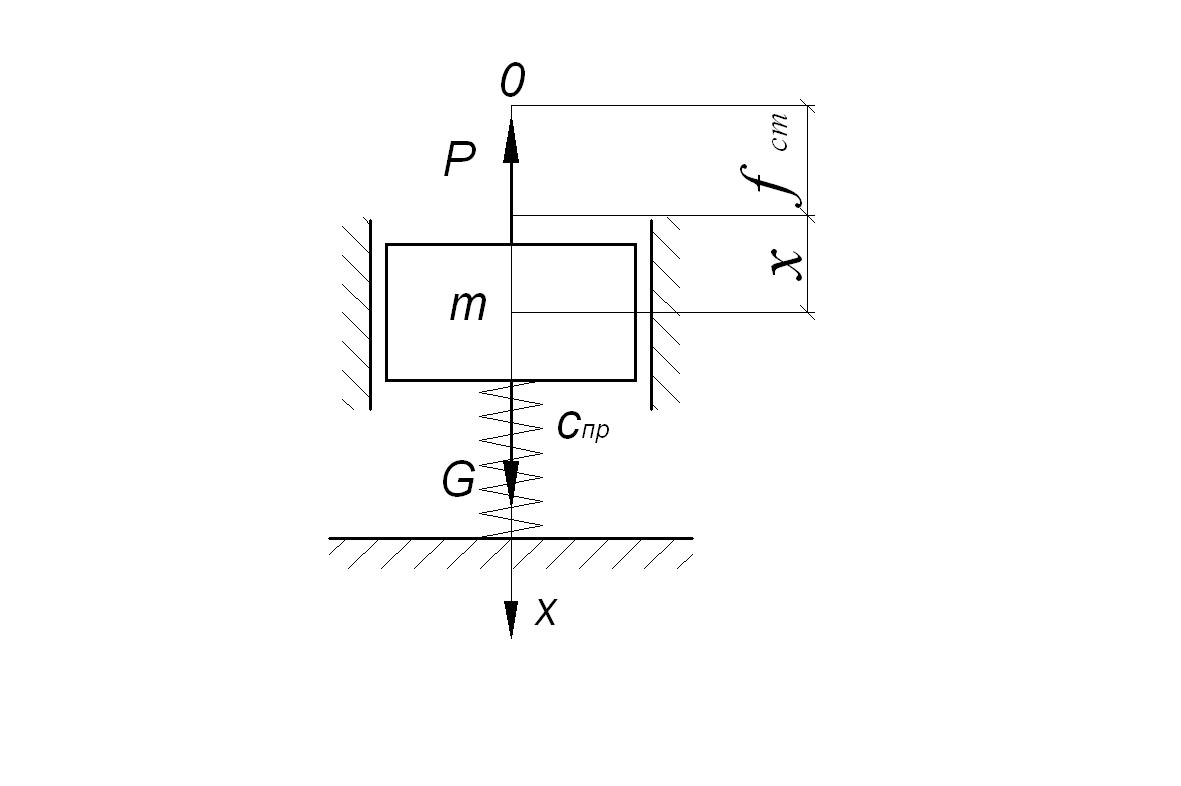
Динамическая модель системы после проведенных преобразований будет иметь вид, показанный на рисунке 2.2, а. Предположим, что материальная точка М выведена из положения равновесия некоторой внешней нагрузкой F, направленной вниз. Изобразим материальную точку в текущем положении с приложенными к ней силами (рисунок 1.2). После снятия нагрузки F, имеющей импульсный характер, на массу m действуют сила тяжести G, направленная вниз, и сила упругости P, направленная противоположно деформации пружины (рисунок 2.2, б).

а)	б)

Рисунок 2.2 – Расчетная схема динамической системы

Запишем основное уравнение динамики в проекции на ось х, направленную вертикально вниз:

(2.2)

где Р_х – сила упругости пружины в проекции на ось х, равная

(2.3)

Здесь - статическая деформация пружины; х – текущая координата.

Подставим в дифференциальное уравнение движения (2.2) значение силы упругости:

Получаем уравнение движения в виде:

Введем обозначение:

(2.4)

Величина к называется циклической частотой свободных колебаний.

Тогда уравнение движения примет вид:

(2.5)

Для интегрирования однородного линейного уравнения с постоянными коэффициентами (2.5) воспользуемся подстановкой Эйлера. Решение уравнения будем искать в виде: , тогда , .

Подставив полученные выражения в уравнение (2.5), получим характеристическое уравнение:

Корни характеристического уравнения равны:

,

Поскольку корни – комплексные числа, то решение уравнения (2.5) будем искать в виде:

(2.6)

Для определения констант интегрирования С₁ и С₂ продифференцируем уравнение (2.6) по времени:

(2.7)

Согласно исходным данным, в начальный момент времени (t = 0) точка имеет координату x₀ и скорость . Тогда, подставив эти начальные условия (t = 0: x = x₀, ) в уравнения (2.6) и (2.7), найдем:

,

Откуда

,

Подставив найденные значения констант интегрирования С₁ и С₂ в уравнение (2.6), окончательно получим уравнение движения материальной точки М в виде:

(2.8)

Для исходных данных имеем:

; к=0,283 рад/с.

(2.9)

Придадим уравнению (2.6) другой вид, введя вместо констант С₁ и С₂ другие постоянные А и β, положив:

Подставив эти значения С₁ и С₂ в уравнение (2.6), будем иметь:

Последнее уравнение можно привести к виду:

(2.10)

Уравнение (2.10) является уравнением гармонического колебательного движения точки, в котором величина А называется амплитудой, а β – начальной фазой колебаний.

Амплитуда А и начальная фаза β свободных колебаний материальной точки как постоянные интегрирования, введенные вместо С₁ и С₂, определяются по начальным условиям движения. Продифференцировав уравнение (2.10) по времени, получим выражение, определяющее скорость точки М:

(2.11)

Подставив в уравнения (2.10) и (2.11) начальные условия, получим:

откуда найдем значения констант интегрирования А и β:

(2.12)

(2.13)

Для исходных данных получим:

м; .

Тогда уравнение движения (2.10) запишется в виде:

(2.14)

Период свободных колебаний определяется по формуле:

(2.15)

с

По уравнению (2.9) или (2.14) строим график свободных колебаний. На рисунке 2.3 показан график свободных колебаний материальной точки М, построенный в программном пакете Mathsoft Mathcad 11.

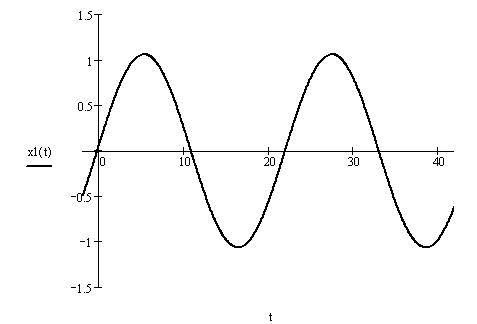
Рисунок 2.3 – График свободных колебаний материальной точки