2. Математические модели управления
2.1. Модель управления ценообразованием
Задача обоснования цены на производимую продукцию сводится к нахождению такой цены, которая бы обеспечивала максимальную прибыль. Для построения экономико-математической модели обоснования оптимальной цены введем обозначения:
х – проданная цена единицы продукции;
S – полная себестоимость единицы продукции;
N(х) = ах + b – прогноз кривой спроса.
Тогда формулы для издержек валовой выручки и финансового результата имеют вид:
U(х) = S N(x) = S a x + S b
B(х) = x N(x) = a x2 + b x
(х) = B – U = a x2 + (b a S) x S b
Задача определения оптимальной цены х* сводится к нахождению максимума функции (х).
Оптимальный объем производства определяется по формуле
N* = a x* + b
Формулу зависимости прогноза спроса от цены N(x) = ax + b можно получить на основе таблично-заданного спроса.
-
х
x1
x2
N
N1
N2
где: х1, х2 – возможные цены; N1, N2 – соответствующие значения спроса.
Коэффициенты а и b при этом определяются по формулам:
;
b
= N1
a
x1
Задание 4. Найти оптимальную цену единицы продукции и оптимальный объем производства при следующих исходных данных.
Варианты |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
х1 [руб/шт] |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
х2 [руб/шт] |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
N1 [шт] |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
N2 [шт] |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
S [руб/шт] |
0,8 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
2.2. Модель транспортно – складского хозяйства (управление товарными запасами).
Для построения экономико – математической модели (эмм) введём обозначения: СХР – стоимость хранения на складе единицы товара за единицу времени, [руб/(шт×сутки)]; Х0 – размер партии [шт], завозимой на склад с периодичностью ТЦ [сутки]; Т – длительность рабочего периода [сутки]; М – общее количество товара [шт], проходящее через склад за время Т; n – число партий, завозимых на склад за время Т; V = dX/dt – интенсивность потребления товара со склада [шт/сутки]; СТР – стоимость перевозки одной партии товара размером Х0, [руб/партия]; СТР.0 – постоянная составляющая перевозки одной партии товара [руб/партия]; СТР.УД – стоимость перевозки одной штуки товара [руб/шт]; З, ЗХР, ЗТР – затраты общие, хранения и транспортировки соответственно [руб]; ХСР – среднее количество товара [шт], находящееся на складе в течение времени ТЦ.
Модель строится на следующих уравнениях.
З = ЗХР + ЗТР (1).
ЗХР = ХСР ∙ Т ∙ СХР (2).
ХСР
=
∙
∙
dt
(3).
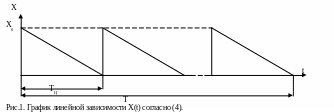
При Х(t) – линейная функция: Х = Х0 – V ∙ t (рис.1), то ХСР = Х0/2 (4).
СТР = СТР.УД ∙ Х0 + СТР.0 (5).
ЗТР = n ∙ СТР (5.1).
n
=
(6.1).
n
=
(6.2).
После следующих преобразований:
(6.1) Þ
n
→ (6.2) Þ
ТЦ:
ТЦ
= Т ∙
(7).
(4) Þ
ХСР
→ (2) Þ
ЗХР:
ЗХР
=
∙
Х0
(8);
(6.1) Þ
n
→ (5.1); (5) Þ
СТР
→ (5.1) Þ
ЗТР:
ЗТР
=
+
М∙СТР.УД
(9).
(8) Þ ЗХР → (1); (9) Þ ЗТР → (1).
Тогда: З = ∙ Х0 + + М∙СТР.УД (10).
Для нахождения минимального значения З = ЗMIN при оптимальном значении Х0 = Х0* необходимо выполнить следующие действия:
(10) Þ
= 0 Þ
Х0
= Х0*.
Тогда:
Х0*
=
(11); ЗMIN
=
+
М∙СТР.УД
(12).
Оптимальное значение ТЦ = ТЦ* определится при подстановке в (7): Х0 = Х0* из (11). Тогда:
ТЦ*
=
(13).
Графики зависимостей: ЗХР(Х0) согласно (8), ЗТР(Х0) согласно (9), З(Х0) согласно (10) показаны на рис.2.
Примечание.
Формула (3)следует из следующих рассуждений. Затраты за хранение товара в количестве “X” штук в течение времени ТЦ можно определить:
ЗХР = ХСР ∙ ТЦ ∙ СХР или ЗХР = СХР ∙ ∙ dt
Отсюда получим: ХСР = ∙ ∙ dt.
Задание 5. Определить оптимальный размер транспортной партии Хо*, период подвоза Тц и соответствующие затраты З. Значения входных параметров согласно вариантов заданы в таблице.
№ вар |
М |
Т |
СТР.0 |
СТР.УД |
СХР |
01 |
1500 |
5 |
2 |
0,1 |
0,1 |
02 |
|
6 |
|
0.2 |
|
03 |
|
7 |
|
0,3 |
|
04 |
|
8 |
|
0,4 |
|
05 |
|
9 |
|
0,5 |
|
06 |
1600 |
10 |
2,5 |
0,1 |
0,15 |
07 |
|
11 |
|
0.2 |
|
08 |
|
12 |
|
0,3 |
|
09 |
|
13 |
|
0,4 |
|
10 |
|
14 |
|
0,5 |
|
11 |
1700 |
15 |
3 |
0,1 |
0,2 |
12 |
|
16 |
|
0.2 |
|
13 |
|
17 |
|
0,3 |
|
14 |
|
18 |
|
0,4 |
|
15 |
|
19 |
|
0,5 |
|
16 |
1800 |
20 |
3,5 |
0,1 |
0,25 |
17 |
|
21 |
|
0.2 |
|
18 |
|
22 |
|
0,3 |
|
19 |
|
23 |
|
0,4 |
|
20 |
|
24 |
|
0,5 |
|
21 |
1900 |
25 |
4 |
0,1 |
0,3 |
22 |
|
26 |
|
0.2 |
|
23 |
|
27 |
|
0,3 |
|
24 |
|
28 |
|
0,4 |
|
25 |
|
29 |
|
0,5 |
|
26 |
2000 |
30 |
4,5 |
0,1 |
0,35 |
27 |
|
5 |
|
0.2 |
|
28 |
|
6 |
|
0,3 |
|
29 |
|
7 |
|
0,4 |
|
30 |
|
8 |
|
0,5 |
|
31 |
2100 |
9 |
5 |
0,1 |
0,4 |
32 |
|
10 |
|
0.2 |
|
33 |
|
11 |
|
0,3 |
|
34 |
|
12 |
|
0,4 |
|
35 |
|
13 |
|
0,5 |
|
36 |
2200 |
14 |
5,5 |
0,1 |
0,45 |
37 |
|
15 |
|
0.2 |
|
38 |
|
16 |
|
0,3 |
|
39 |
|
17 |
|
0,4 |
|
40 |
|
18 |
|
0,5 |
|