1. Математические методы прогнозирования случайного параметра
1.1. Прогнозирование на основе статистического материала
Параметр называется случайным, если мы не можем точно сказать, какое он примет значение в будущем. Прогнозирование случайного параметра х сводится к нахождению оценок его среднего значения и дисперсии. Указанные характеристики определяются по формулам:
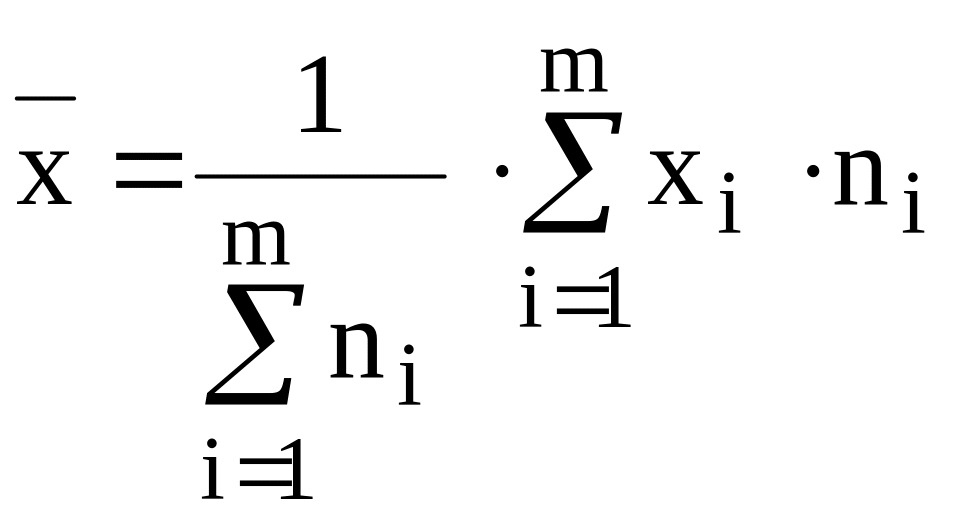
среднее
значение;
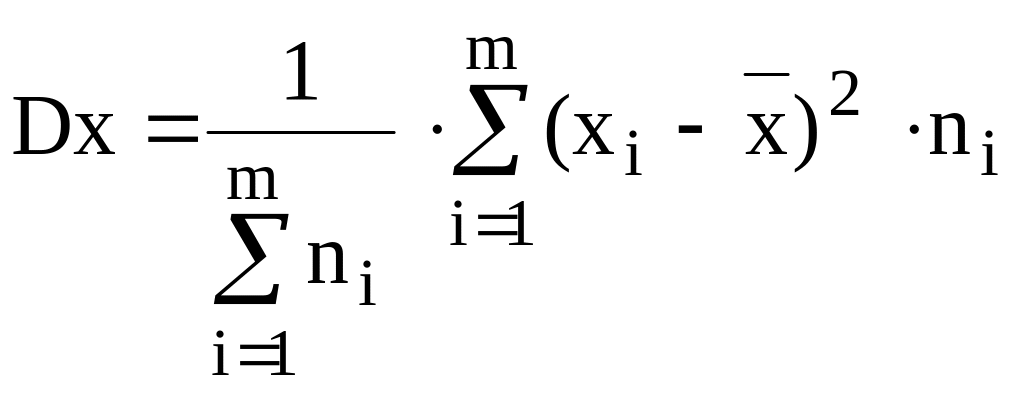
дисперсия,
где хi – i-ое значение параметра х;
ni – абсолютная частота хi-го значения;
m – число значений параметра х.
Наряду с этим вычисляются также:
среднее
квадратичное отклонение
коэффициент
вариации.
Если
в качестве прогнозного значения параметра
х применяется
,
то абсолютная ошибка прогноза
=
вычисляется по формуле:
=
0,78 ∙
Х;
относительная ошибка прогноза вычисляется по формуле:
х
=
100% =0,78
Vх
100%
Задание 1
На основе обработки статистического материала были получены следующие данные о параметре х (табл. 1.1.). Требуется определить прогноз параметра х и оценить относительную ошибку прогноза х.
Таблица 1.1.
Варианты исходных данных задания 1
№ варианта |
ni |
5 |
10 |
18 |
36 |
19 |
9 |
3 |
xi |
||||||||
0 |
xi |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
1 |
xi |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
2 |
xi |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
3 |
xi |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
4 |
xi |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
5 |
xi |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
6 |
xi |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
7 |
xi |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
8 |
xi |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
9 |
xi |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
Здесь и далее номер варианта соответствует последней цифре номера зачетной книжки студента.
1.2. Прогнозирование методом экспертных оценок
Среднее
значение (
)
и дисперсия (Dx)
параметра X
на основе экспертных оценок вычисляются
по формулам.
Если эксперт может оценить два значения прогнозируемого параметра: ХMIN и XMAX, то исходя из гипотезы о равномерной плотности вероятностей, задаваемой двумя параметрами ХMIN и XMAX:
,
.
Если эксперт может оценить три значения прогнозируемого параметра: ХMIN, Х0 , XMAX, то исходя из гипотезы о нормальной плотности вероятностей, задаваемой тремя параметрами ХMIN, Х0 , XMAX:
,
;
где: Xmin – минимально возможное значение параметра X;
Xo – наивероятнейшее значение параметра X;
Xmax – максимально возможное значение параметра X.