2. Построение минимаксных решающих правил (решение статистической игры)

Непосредственное построение минимаксных решающих правил по определению, приведенному в п. 3.1, обычно бывает затруднительным. Поэтому используют два основных подхода к решению статистической игры.

1. Первый подход к отысканию минимаксных решающих правил основан на свойствах наименее благоприятного априорного распределения.

Теорема 1. Если статистическая игра имеет значение и если есть наименее благоприятное априорное распределение состояний природы , то каждое минимаксное решающее правило будет байесовским относительно .

Если множество априорных распределений имеет достаточно простую структуру - например. при имеем

,

то нетрудно найти наименее благоприятное априорное распределение. используя вогнутость минимального байесовского риска .

Часто можно сделать некоторое разумное предположение относительно , найти соответствующее байесовское решающее правило , а затем убедиться, является ли оно минимаксным, пользуясь следующим утверждением.

Теорема 2. Если решающее правило является байесовским относительно некоторого априорного распределения и для любого имеет место неравенство , то статистическая игра имеет значение , есть минимаксное решающее правило, а - наименее благоприятное априорное распределение.

Иногда удобно пользоваться более общей формулировкой этой теоремы.

Теорема 2а. Пусть в статистической игре распределения вероятностей на принадлежат некоторому подсемейству общего семейства вероятностных мер и пусть для этой игры имеется минимаксное решающее правило , а - значение игры. Тогда, если при любом , то решающее правило будет минимаксным и для более общей статистической игры , в которой .

Если наименее благоприятное априорное распределение не существует, то может быть предпринята попытка построить соответствующую максимизирующую последовательность априорных распределений.

Теорема 3. Пусть - последовательность априорных распределений на и - последовательность соответствующих байесовских решающих правил с байесовскими рисками . Если и существует такое решающее правило , что для любого выполняется неравенство , то есть минимаксное решающее правило, а есть значение игры.

2. Второй подход к отысканию минимаксных решающих правил основан на понятии уравнивающего решающего правила, то есть такого решающего правила , для которого при любом .

Теорема 4. Если решающее правило является уравнивающим с риском и если оно является байесовским относительно некоторого априорного распределения , то есть минимаксное решающее правило, а - наименее благоприятное априорное распределение, причём значение игры равно .

Теорема 5. Если решающее правило является уравнивающим с риском и если существует последовательность априорных распределений такая, что , то есть минимаксное решающее правило.

Пример. Вероятность успеха в распределении Бернулли неизвестна. Требуется выбрать решение на основании одного наблюдения случайной величины при квадратичной функции потерь . Соответствующая статистическая игра может служить, например. математической моделью следующей прикладной задачи: оценить вероятность безотказной работы в течение гарантийного срока для некоторых изделий, выпускаемых предприятием, называя оценку на основании испытания одного образца изделия (с исходом - безотказная работа или - отказ) при потере, пропорциональной квадрату ошибки оценивания.

Таким образом, мы имеем , . Выпуклость функции потерь позволяет сразу исключит рандомизацию (см. п. 5.1). Рассмотрим некоторое нерандомизированное решающее правило . Здесь любое можно представить точкой в единичном квадрате в том смысле, что . Непосредственный выбор наименее благоприятного априорного распределения на затруднителен. Поэтому будем искать среди уравнивающее решающее правило. Функция риска имеет вид:

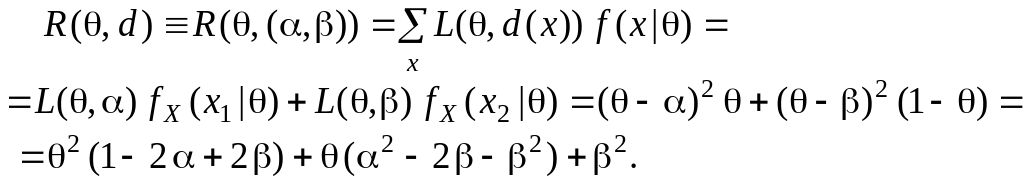
Если решающее правило является уравнивающим, то его риск не зависит от и коэффициенты при и в выражении для должны быть равны нулю:

.

Решая эту систему, находим единственное уравнивающее решающее правило . Оно имеет постоянный риск, равный .

В силу Теоремы 4 это решающее правило будет минимаксным, если оно является байесовским относительно некоторого априорного распределения . Для любого априорного распределения на , имеющего первые два момента и , получим байесовский риск произвольного решающего правила :

Байесовское решающее правило относительно будет описываться точкой , минимизирующей . Значения и найдём из системы уравнений

.

Таким образом, . Уравнивающее решающее правило будет байесовским относительно при . Для этого необходимо и достаточно, чтобы , .

Итак, минимаксное решающее правило в нашей задаче состоит в том, чтобы при оценивать как , а при - как . Значение игры равно и любое априорное распределение на с , является наименее благоприятным.

Упражнения

1. Дайте геометрическую интерпретацию (при конечном ) Теорем 2 и 3 для случая, когда среди минимаксных решающих правил нет уравнивающих правил.

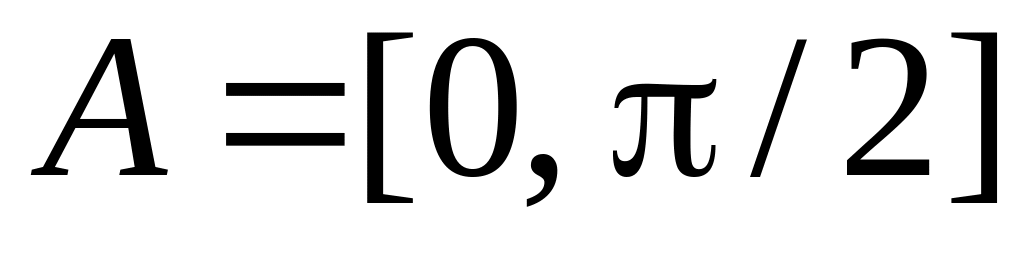2. Пусть , , а функция потерь задаётся соотношениями 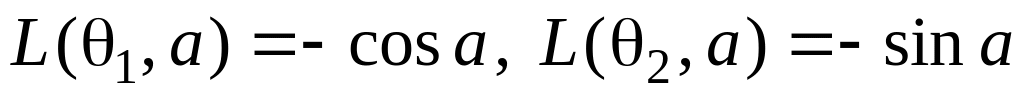. Наблюдаемая случайная величина имеет распределение Бернулли, , с или 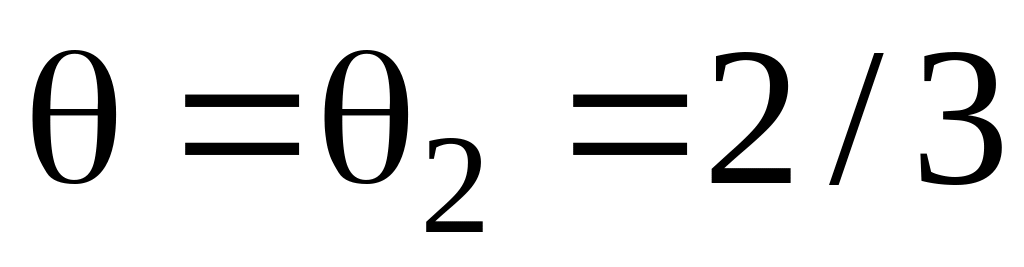в зависимости от состояния природы.

а. Представьте класс нерандомизированных решающих правил как подмножество плоскости , принимая .

б. Найдите и для всех .

в. Найдите байесовское решающее правило относительно априорного распределения , дающего вероятность каждому из состояний природы.

г. Покажите, что есть минимаксное решающее правило и что является наименее благоприятным априорным распределением. Найдите значение игры .

3. Пусть , , а функция потерь задаётся соотношениями . Проводится одно испытание Бернулли с вероятностью успеха или .

а. Покажите, что в этой статистической игре класс нерандомизированных решающих правил является существенно полным и представьте его как подмножество плоскости .

б. Найдите риски и для .

в. Найдите класс всех нерандомизированных байесовских решающих правил и изобразите его на рисунке, как подмножество в .

г. Найдите минимаксное решающее правило в классе всех байесовских решающих правил. Найдите наименее благоприятное априорное распределение и значение игры.

4. Пусть . Наблюдаемая случайная величина имеет геометрическое распределение с функцией вероятностей

а. Запишите функцию риска для решающего правила в виде ряда по степеням .

б. Покажите, что единственное нерандомизированное уравнивающее правило есть .

в. Покажите, что нерандомизированное решающее правило является байесовским относительно априорного распределения тогда и только тогда, когда , где - начальные моменты распределения .

г. Покажите, что решающее правило в (б) является -байесовским, а следовательно – минимаксным. Найдите значение игры.

5. (Г.Н. Дюбин [13]). Задана последовательность испытаний Бернулли с неизвестной статистику вероятностью успеха . После первого успеха статистику сообщается, на каком шаге это произошло. Таким образом, наблюдаемая случайная величина имеет геометрическое распределение с функцией вероятностей и стратегиями природы являются числа . Статистик должен принять решение при квадратичной функции потерь .

Найдите минимаксное решающее правило. наименее благоприятное априорное распределение и значение игры.

6. Оценка вероятности безотказной работы изделий. Пусть вероятность безотказной работы в течение гарантийного срока работы изделий, выпускаемых промышленным предприятием, неизвестна. Оценку этой вероятности при квадратичной функции потерь необходимо сделать на основании независимых испытаний экземпляров изделий. Исходы этих испытаний представляют собой повторную выборку объёма , из распределения Бернулли, , с вероятностью успеха .

а. Покажите, что есть достаточная статистика для и что случайная величина имеет биномиальное распределение .

б. Найдите байесовское решающее правило относительно априорного бета-распределения, имеющего плотность

.

Указания. 1. Покажите, что апостериорное распределение, с плотностью , есть также бета-распределение.

2. Для случайной величины. имеющей бета-распределение с параметрами , математическое ожидание равно .

в. Покажите, что в этой статистической игре класс нерандомизированных решающих правил , основанных на достаточной статистике, является существенно полным.

г. Найдите функцию риска и определите параметры и , при которых байесовское решающее правило будет уравнивающим.

д. Запишите минимаксное решающее правило . определите наименее благоприятное априорное распределение и значение игры. Сравните полученные результаты при с решением задачи, рассмотренной в примере.

е. Найдите оптимальный объём выборки в случае, если стоимость испытания каждого экземпляра изделия равна .

7. (Ходжес и Леман [14]). Пусть - независимые случайные величины, одинаково распределённые на , причём их распределение полностью неизвестно, то есть, , где - общее семейство распределений на . Пусть и задача состоит в получении оценки неизвестного математического ожидания при квадратичной функции потерь . Используя решение упр. 6 и Теорему 2а, покажите, что в этой задаче непараметрического статистического оценивания минимаксное решающее правило имеет вид

.

8. Пусть , и, наблюдая повторную выборку объёма из нормального распределения с известной дисперсией , статистик должен принять решение о неизвестном среднем .

а. Покажите, что статистика является достаточной для и найдите её распределение.

б. Покажите, что в этой статистической игре класс нерандомизированных решающих правил , основанных на достаточной статистике, является существенно полным.

в. Найдите байесовские решающие правила относительно последовательности нормальных априорных распределений с нулевым средним и дисперсией . Определите соответствующую последовательность минимальных байесовских рисков .

г. Найдите минимаксное решающее правило и значение игры .

9. Пусть и статистик должен принять решение после наблюдения повторной выборки объёма из распределения Пуассона с неизвестным параметром .

а. Покажите, что среднее арифметическое есть уравнивающее решающее правило.

б. Найдите байесовские решающие правила относительно априорных гамма-распределений с плотностью (для ):

.

Указания. 1. Покажите, что апостериорное распределение, с плотностью , есть также гамма-распределение.

2. Для случайной величины. имеющей гамма-распределение с параметрами , математическое ожидание равно , а дисперсия равна .

в. Покажите, что решающее правило из (а) есть -байесовское, а следовательно – минимаксное решающее правило. Найдите значение игры.

10. Обнаружение радиолокационной цели. Пусть результаты наблюдений величины сигнала на выходе приёмника радиолокационной станции в моменты времени описываются случайным вектором с , где , это независимые случайные величины ("шум"). имеющие одинаковое нормальное распределение с известной дисперсией и нулевым средним. - "полезный" сигнал, причём соответствует отсутствию цели в зоне обзора, а соответствует наличию цели. Таким образом, здесь , а множество решений статистика состоит из двух элементов , означающих: - цель не обнаружена, - цель обнаружена. Если "ложная тревога" (принятие решения при ) приводит к потере, равной , а пропуск цели (принятие решения при ) – к потере, равной , то функцию потерь можно представить в виде матрицы

Θ
	0
		0

:

а. Показать, что достаточной статистикой для неизвестного состояния природы будет ; найти распределение случайной величины .

б. Найти байесовское решающее правило относительно априорного распределения, описываемого вектором , где есть априорная вероятность появления цели , то есть, . Выразить это байесовское решающее правило в виде простого "порогового" соотношения для наблюдаемого значения достаточной статистики .

в. Найти риск этого байесовского решающего правила.

г. Показать, что нерандомизированные решающие правила, основанные на достаточной статистике, составляют в этой статистической игре существенно полный класс.

д. Найти минимаксное решающее правило, наименее благоприятное априорное распределение и значение игры, в частности, для случая .