2. Условия исключения рандомизации в статистических играх

Если в статистической игре функция потерь непрерывна и выпукла по при любом и при , то класс нерандомизированных решающих правил является существенно полным. При этом для любого решающего правила можно найти не худшее нерандомизированное правило как . Здесь усреднение производится по соответствующей смешанной стратегии статистика:

- при ;

- при .

Пример. Пусть множество выборок содержит только точек, невыпуклая функция равна нулю, если и равна единице в остальных случаях, а и совпадает с конечным отрезком вещественной прямой, имеющим длину, превышающую . Очевидно, здесь для нерандомизированных решающих правил минимаксный риск равен единице, поскольку природа может выбрать так, чтобы для любого решения статистика . Однако, допуская рандомизацию, мы можем уменьшить минимаксный риск, даже не используя результаты наблюдений : если наше случайно выбираемое решение будет равномерно распределено по всему отрезку , то максимальный риск составит (длину отрезка ).

Если в статистической игре множества и конечны, а функции абсолютно непрерывны для любого , то для всякого решающего правила существует эквивалентное нерандомизированное правило , то есть класс нерандомизированных решающих правил является существенно полным.

Упражнения

1. Пусть и . Пусть для каждого наблюдаемая случайная величина имеет геометрическое распределение с функцией вероятностей Найдите нерандомизированное решающее правило , которое имеет меньший риск, чем рандомизированное решающее правило , выбирающее 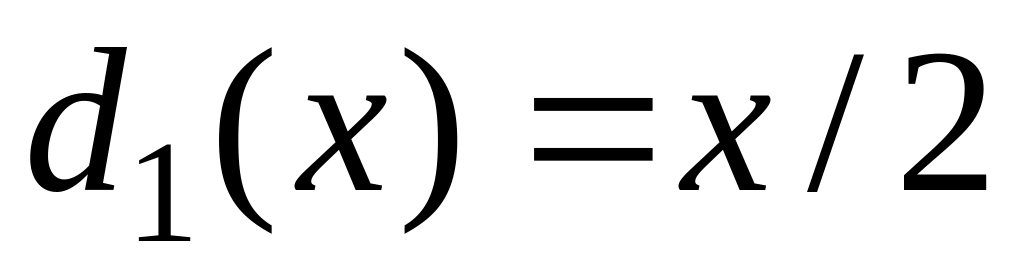и 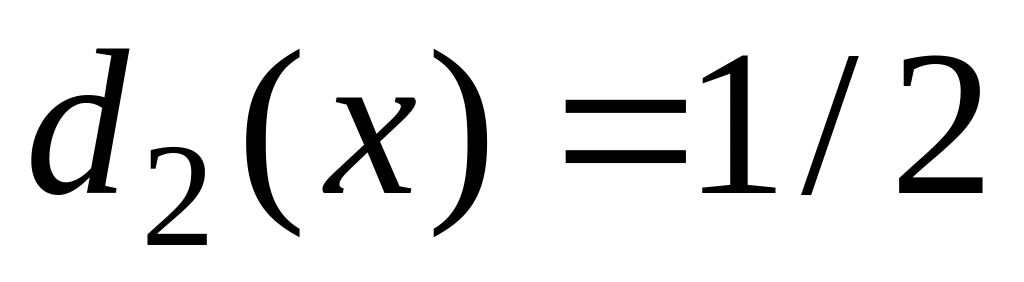с вероятностями каждое. Найдите функции риска и .

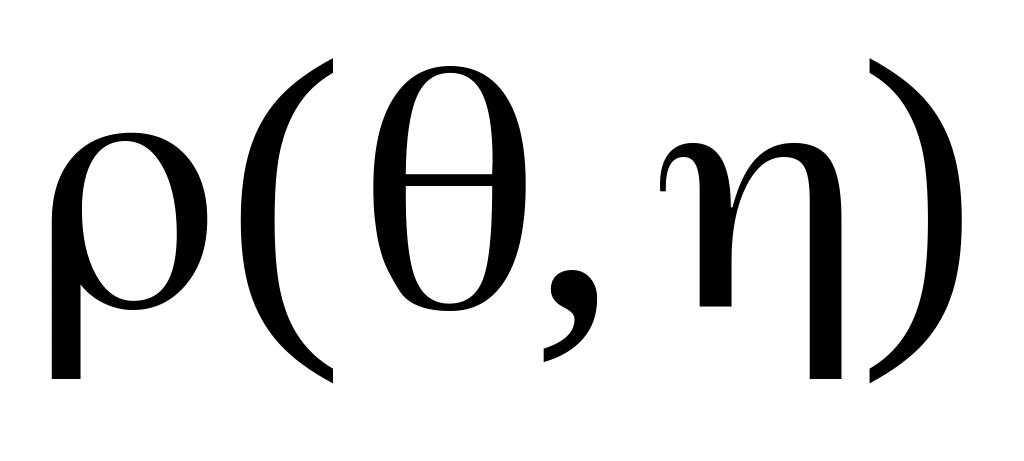2. Пусть и . Наблюдаемая случайная величина имеет распределение Бернулли 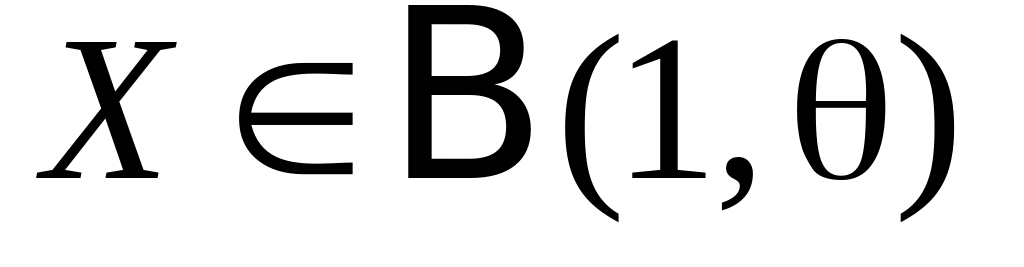, с неизвестной вероятностью успеха . Найдите нерандомизированное решающее правило , не худшее рандомизированного правила из упр. 1. Найдите функции риска и .

3. (Ходжес и Леман [14]). Пусть и пусть , причём наблюдаемая случайная величина имеет биномиальное распределение с известным и неизвестным . Функция потерь , является вогнутой функцией от 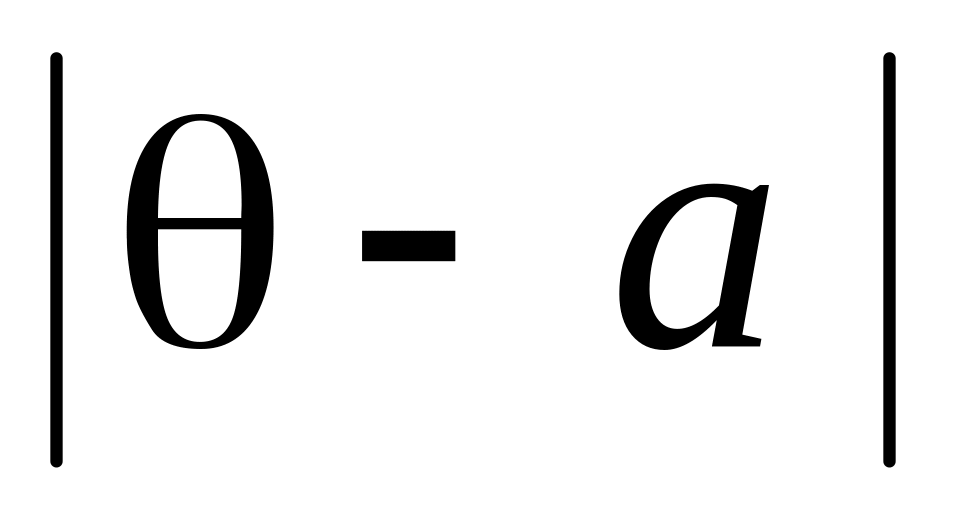. Покажите, что в такой задаче класс нерандомизированных решающих правил не является существенно полным.

4. Построение оптимальных решающих правил

   1. Построение байесовских решающих правил

Если оптимальные (минимаксные) решающие правила в статистической игре существуют, то они принадлежат классу байесовских решающих правил. Кроме того, байесовские стратегии находят непосредственное применение во многих статистических задачах, содержащих априорную вероятностную информацию о неизвестном состоянии природы.

Нерандомизированные байесовские решающие правила составляют существенно полный подкласс в классе всех байесовских правил относительно данного априорного распределения .

Чтобы построить нерандомизированное байесовское решающее правило относительно данного априорного распределения , то есть обеспечить , следует при каждом наблюдении случайной величины (случайного вектора) выбирать решение , минимизирующего апостериорный условный риск

Здесь функция апостериорного распределения характеризуется плотностью или функцией вероятностей , вычисляемой по формуле Байеса

, ,

где , , - это плотности или функции вероятностей априорного распределения состояний природы , условного распределения наблюдаемой случайной величины при данном и маргинального (безусловного) распределения , соответственно.

Заметим, что байесовский риск решающего правила и апостериорный условный риск связаны очевидным соотношением

,

где - функция безусловного распределения для .

Минимальный байесовский риск является вогнутой функцией от .

Пример 1. Пусть в исходной антагонистической игре , , а функция потерь описывается матрицей

Θ
	0
		0

:

Распределения вероятностей наблюдаемой случайной величины характеризуются плотностями или функциями вероятностей . Соответствующая статистическая игра – это задача проверки простой гипотезы против простой гипотезы при стоимости ошибок , . Найдём байесовское решающее правило относительно априорного распределения , заданного априорной вероятностью состояния природы .

По формуле Байеса

,

то есть

, .

Апостериорный условный риск в этой задаче равен

,

или

, .

При любом следует принимать , если и в случае обратного неравенства. Таким образом, байесовское решающее правило относительно при любом заданном значении имеет вид

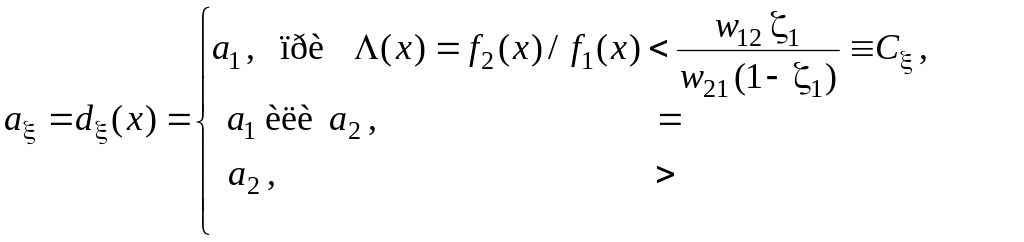
Функцию называют отношением правдоподобия.

Пример 2. Пусть и необходимо оценить неизвестный параметр семейства распределений , объявляя решение при квадратичной функции потерь , после наблюдения случайной величины . Найдём в такой задаче статистического оценивания байесовское решающее правило относительно априорного распределения , характеризуемого плотностью .

При любом значении имеем , где .

В нашем примере . Минимизируем эту функцию, дифференцируя по и приравнивая производную нулю, что даёт

.

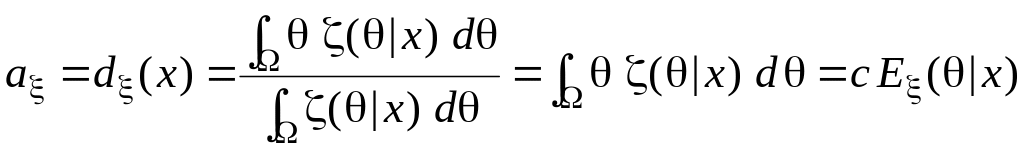Из проделанных выкладок следует, что

,

а минимальный байесовский риск равен

,

где математическое ожидание берётся по безусловному распределению случайной величины .

Упражнения

1. Пользуясь приведенными соотношениями, найдите байесовское решающее правило в задаче иллюстративного примера п. 1.3, если известна априорная вероятность плохой погоды в летние дни.

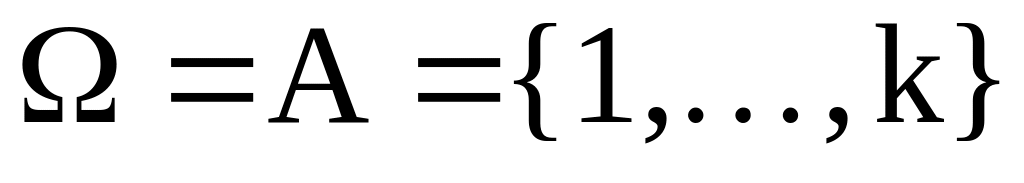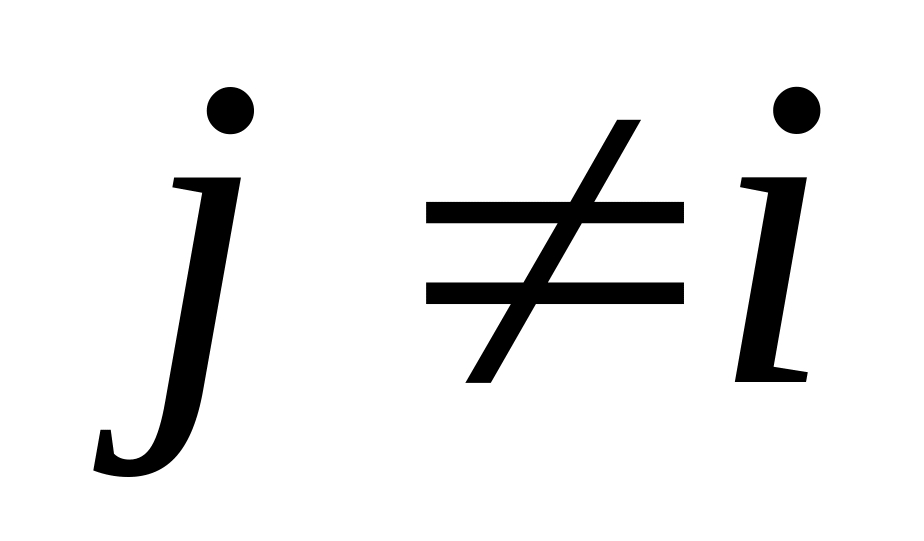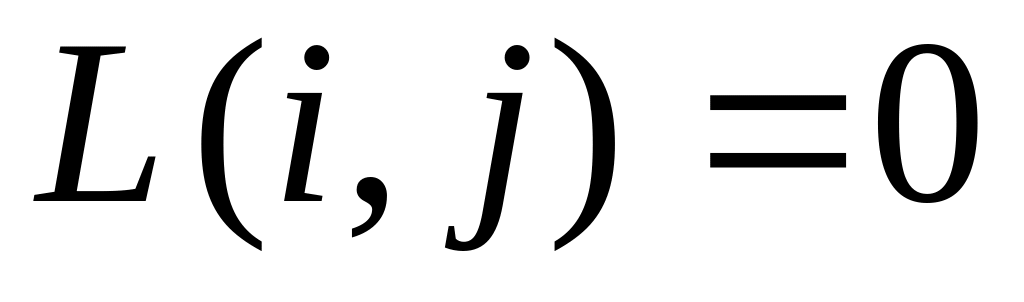2. Пусть в статистической игре множества и конечны, , а функция потерь имеет вид (так называемая задача классификации): при , при 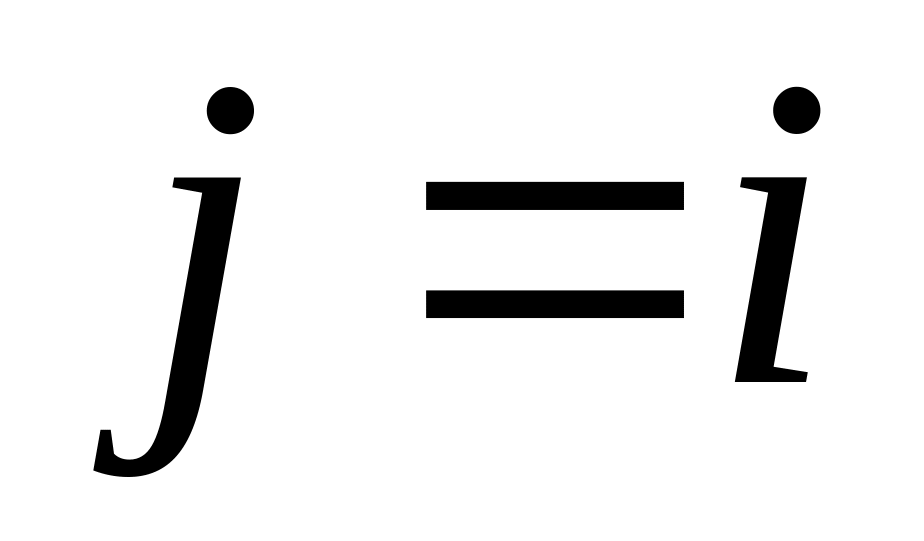, . Найдите байесовское решающее правило относительно заданного априорного распределения с .

3. Контроль качества продукции в текстильном производстве. Нужно оценить среднее число дефектов на 1 метр ткани в данной партии продукции на основании подсчёта числа дефектов на метрах ткани в случайным образом отобранных рулонах, при квадратичной функции потерь. Здесь 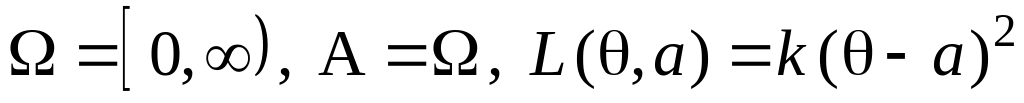, а наблюдаемая случайная величина 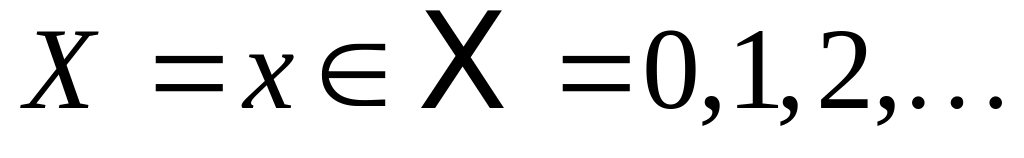имеет распределение Пуассона с функцией вероятностей

Пусть по результатам многолетнего статистического контроля известно среднее число дефектов на метр ткани, характеризующее данный технологический процесс, и априорное распределение неизвестного параметра имеет плотность .

а. Найдите байесовское решающее правило относительно .

б. Пусть потеря исчисляется в рублях, а стоимость подсчёта числа дефектов на каждом метре ткани составляет рублей. Найдите минимальный байесовский риск и определите оптимальный объём контроля , при котором суммарные затраты будут минимальными.

4. Найдите байесовское решающее правило относительно заданного в задаче примера 2 априорного распределения, если функция потерь имеет вид:

а)

б) .