3.2. Геометрическая интерпретация статистической игры при конечном множестве

Если множество состояний природы конечно, , то каждому решающему правилу можно поставить в соответствие -век­тор риска . Множеством рисков в статистической игре называется разбиение

.

Множество рисков является выпуклой оболочкой множества нерандомизированных рисков

и описывает статистическую игру с конечным с точностью до эквивалентных решающих правил. Крайние точки выпуклого множества S соответствуют нерандомизированным решающим правилам.

Для конечного любое априорное распределение может быть представлено в виде -вектора

с .

Байесовский риск любого правила относительно априорного распре­деления равен

и одинаков для всех точек гиперплоскости . Байесовскому правилу соответствует . Поэтому все байесовские решающие правила относительно заданного могут быть представлены точками границы выпуклого множества рисков S, общими с опорной гиперплоскостью . Величина минимального байесовского риска определяется координатами точки пересечения этой опорной гиперплоскости с прямой (см. рис. 1).

Рис. 1

Из этой геометрической интерпретации следует, что для любого байесовского решающего правила относительно заданного существует хотя бы одно эквивалентное нерандомизированное байесовское правило (крайняя точка множества рисков S) относительно того же .

Точки пересечения границы множества

с множеством рисков S соответствуют решающим правилам , эквивалентным по максимальному риску . Поэтому минимаксные решающие правила найдутся как точки пересечения множества рисков S с наименьшим множеством , для которого (см. рис. 2).

Рис. 2

Величина есть значение статистической игры (минимаксный риск) v. Из этой геометрической интерпретации следует, что минимаксное решающее правило , если оно существует, совпадает с байесовским решающим правилом относительно наименее благоприятного априорного распределения , причём , и что может не существовать нерандомизированное решающее правило (точка может не являться крайней точкой выпуклого множества S).

Упражнения

1. Дайте геометрическую интерпретацию статистической игры иллюстративного примера п. 1.3. Покажите на соответствующих рисунках результаты решения упражнений 1 и 2 п.3.1.

2. Для случая 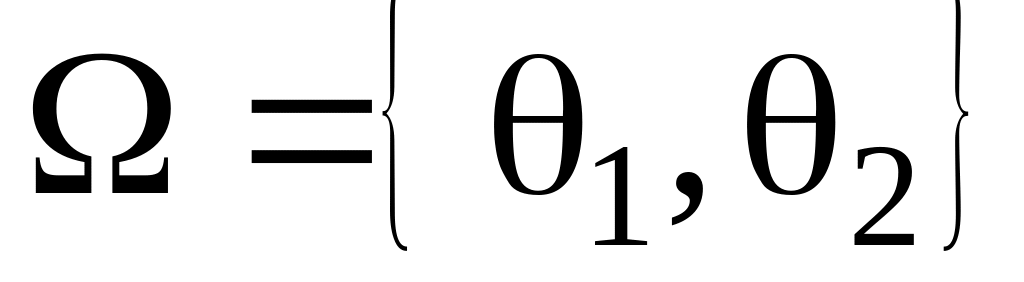покажите на рисунках множества рисков S статистических игр с неединственным байесовским решающим правилом, игр с неединственным минимаксным решающим правилом.

4. Редукция класса решающих правил

Существует ряд подходов к редукции общего класса решающих правил в статистической игре и выделения некоторого полного (или существенно полного) подкласса, в котором затем могут быть найдены оптимальные стратегии статистика. Здесь мы рассмотрим возможности замены в решающих правилах многомерного вектора выборки достаточной статистикой меньшей размерности и условия, при которых можно отказаться от рандомизации решающих правил. Приобретение навыков в построении достаточных статистик и выявления возможностей отказа от рандомизации облегчит последующее овладение практическими приёмами решения упражнений на отыскание байесовских и минимаксных решающих правил. Другим способам редукции класса решающих правил в статистических играх, таким, как применение принципа инвариантности и использование монотонных решающих правил, посвящены отдельные разделы данного пособия.