4. 3. 3. Устойчивые и неустойчивые резонаторы.
Гауссовы резонаторы. Линзовые волноводы и открытые резонаторы. Анализируя различные конфигурации открытых резонаторов, можно увидеть, что одни из них хорошо "удерживают" излучение внутри себя при многократном прохождении его между зеркалами резонатора, обладают малыми дифракционными потерями, другие же наоборот, плохо "удерживают" такое излучение, имеют большие дифракционные потери. Причем то, какими из указанных свойств обладает резонатор, полностью определяется его конфигурацией: радиусами кривизны зеркал и расстоянием между ними, а также апертурными размерами зеркал. Чтобы проследить это, воспользуемся тем обстоятельством, что между открытыми резонаторами и линзовыми волноводами существует весьма близкая аналогия [3], а при рассмотрении хода световых лучей в линзовом волноводе будем пользоваться параксиальным приближением, полагая малым угол между оптической осью волновода (резонатора) и световыми лучами.
Рассмотрим
резонатор длиной 
,
образованный
двумя
вогнутыми
сферическими зеркалами с радиусами
кривизны
и
(рис. 15, а); фокусные расстояния зеркал
равны соответственно 
и 
.
Вогнутое зеркало с фокусным расстоянием
,
оптически эквивалентно комбинации из
плоского зеркала и плоско-выпуклой
линзы, имеющей фокусное расстояние 
(поскольку при такой замене излучение
дважды проходит через линзу: при падении
на зеркало и отражении от него). В связи
с этим резонатор, изображенный на рис.
15, а, можно заменить резонатором,
показанным на рис. 15, б, где вместо
вогнутых зеркал используются указанные
выше комбинации из плоского зеркала и
плоско - выпуклой линзы.
Перейдем теперь от резонатора, изображенного на рис.
15.
б к волноводу, составленному из
двояковыпуклых линз с чередующимися
фокусными расстояниями 
и 
,
расстояние между которыми равно 
(рис.
15, в). Система на рис. 15, в оптически
эквивалента системе на рис. 15, б, а
следовательно, и на рис. 15, а. Правда, в
системах на рис. 15, а, б световая волна
изменяет направление своего распространения
на обратное всякий раз, когда достигает
зеркала, а в системе на рис. 15, в она
распространяется в одном направлении.
Рис. 15. Аналогия резонатора и линзового волновода
Итак, открытый резонатор, образованный сферическими
зеркалами
с радиусами кривизны
и
оптически эквивалентен линзовому
волноводу, состоящему из линз с
чередующимися фокусными расстояниями
и 
.
Шаг волновода (расстояние между соседними
линзами) равен длине резонатора. Вогнутому
зеркалу резонатора соответствуют в
волноводе собирающие линзы, выпуклому
- рассеивающие линзы.
Отличие линзового волновода от резонатора состоит в
том, что резонатор выделяет определенные (дискретные) частоты, в нем устанавливаются стоячие волны, тогда как для волновода характерны непрерывный спектр частот и бегущая волна. В остальном же резонатор и волновод аналогичны друг другу. Как и в резонаторе, в волноводе возбуждаются и поддерживаются характерные распределения поля в поперечном сечении.
Аналогом симметричного конфокального резонатора
является
линзовый волновод, показанный на рис.
16, а (конфокальный линзовый волновод).
Все линзы такого волновода имеют
одинаковое фокусное расстояние 
,
причем шаг волновода равен удвоенному
фокусному расстоянию 
.
В качестве примера на рисунке показаны
два световых луча, распространяющихся
в рассматриваемом волноводе. На примере
этих лучей можно видеть, что конфокальный
волновод способен проводить (канализировать)
излучение - в нем существуют лучи, которые
не выходят за пределы волновода (через
боковую границу волновода).
Линзовый волновод, способный удерживать излучение,
называют устойчивым. Ему соответствует устойчивый резонатор. Наряду с устойчивыми существуют также волноводы, в которых световые лучи отклоняются от оси все больше и больше и в результате покидают волновод. На рис. 16,б приведен пример такого волновода, соответствующего резонатору с выпуклыми зеркалами. Эти волноводы называют неустойчивыми, а соответствующие им резонаторы - неустойчивыми резонаторами.
Анализируя ход лучей в различных волноводах,
соответствующих различным резонаторам, можно получить следующее условие устойчивости открытых резонаторов:
,
(58)
где
;
.
Если
параметры
и
открытого резонатора
удовлетворяют условию (58), то такой резонатор способен удерживать внутри себя излучение, в противном случае резонатор не удерживает внутри себя излучение (даже при условии, что оба зеркала являются полностью отражающими).
Условие устойчивости часто представляют графически,
используя координатную плоскость с осями, на которых
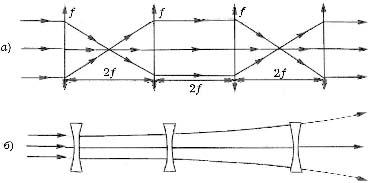
Рис. 16. Ход лучей: а - в устойчивом (конфокальном) волноводе, б - в неустойчивом
откладываются
значения
и
(см.,
например, [8]) - так называемая диаграмма
устойчивости резонаторов.
Такие
резонаторы, как плоскопараллельный
,
конфокальный
,
полуконфокальный
,
концентрический
,
полуконцентрический
,
являются устойчивыми и попадают на
границу устойчивости. Это означает, что
дифракционные потери в них чувствительны
(особенно при больших числах Френеля)
к отклонениям от теоретически идеальных
значений. Поэтому на практике предпочитают
заведомо отклониться в область
устойчивости. Разумеется, это невозможно
в случае плоскопараллельного резонатора.
Перейдем теперь к рассмотрению мод устойчивых
резонаторов, составленных из плоских и сферических зеркал, а также рассмотрим особенности неустойчивых резонаторов.
4. 3. 4. Моды устойчивых резонаторов. В качестве
примера выпишем нормированные распределения плотности потока излучения на отражающих поверхностях для различных мод для плоских резонаторов с прямоугольной (59) и круглой (60) апертурой:
,
(59)
.
(60)
Здесь
- текущие
прямоугольные координаты в
сечении
пучка; 
и
- размеры апертуры по осям 
и
;
и
- числа Френеля, соответствующие
характерным размерам апертуры, 
- параметр в теории открытых резонаторов
Л. А. Вайнштейна; 
-
радиальный
и угловой индексы моды; 
-
текущие полярные координаты в сечении
пучка; 
-радиус
сечения резонатора; 
- функция Бесселя p-го
порядка; 
-й
корень функции Бесселя p-го
порядка.
В случае использования сферических или сферического
и плоского зеркал в устойчивом резонаторе нормированные распределения плотности потока излучения при двуосевой симметрии сечения резонатора описываются функциями Эрмита - Гаусса:
,
(61)
где
- параметр, характеризующий масштаб
сечения; 
и 
-
полиномы Эрмита порядка, соответствующего
индексу моды. Для типов колебаний низших
порядков полиномы Эрмита таковы:
.
При цилиндрической симметрии резонатора
распределения поля описываются функциями Лагерра - Гаусса:
,
где
- полином Лагерра, причем 
и
-
радиальный и угловой индексы моды
соответственно. Для типов колебаний
низших радиальных порядков полиномы
Лагерра таковы:
(62)
.
Устойчивые резонаторы, поля в которых описываются
функциями (61) или (62), получили название гауссовых. Условие гауссовых резонаторов имеет вид:
.
(63)
Как видно из сопоставления условий (63) и (58),
гауссовы резонаторы являются устойчивыми, но не все устойчивые резонаторы являются гауссовыми. Например, плоский резонатор, будучи устойчивым, не является гауссовым. Заметим также, что конфокальный резонатор, хотя и не удовлетворяет условию (63), представляет собой гауссов резонатор.
Отличительной особенностью распределений (61) и (62)
является
независимость их поперечных размеров
от размеров сечения резонатора. Как
видно из (61) и (62), распределение в основной
моде (
или
)
при
цилиндрической и прямоугольной симметрии
описывается функцией Гаусса. При больших
индексах, соответствующих модам более
высоких порядков, распределения
интенсивности имеют более сложный
характер с периодическим чередованием
экстремумов и описываются полиномами
Эрмита - Гаусса или Лагерра - Гаусса.
Примеры таких распределений приведены
на рис. 17 для некоторых значений индексов
m
и n,
больших нуля.
Как видно из выражений (61) и (62) и рис. 17. число
минимумов
(нулевых) по координате 
равно
,
а
по координате 
равно
.
Соответственно
при варьировании радиальной координаты
число минимумов равно
,
а при варьировании угловой координаты
число
минимумов равно 
.
Ввиду
указанного обстоятельства моды принято
обозначать как
,
где
и 
и
есть введенные целочисленные индексы,
значения которых равны соответственно
числу нулевых минимумов поля по одной
и другой координате, соответствующих
распределению поля
,
а
- число полуволн, укладывающихся на
длине резонатора.
Индексы
и 
называют
поперечными,
а
-
продольным
или аксиальным. Соответственно моды,
характеризуемые индексами 
и 
,
т.е.
,
называютпоперечными,
а если учитывают индекс 
,
то говорят о продольной
-й
моде, относящейся к данной поперечной.
Рис. 17. Примеры распределений поля в модах
Чтобы лучше понять систему обозначения мод, можно
обратиться
к рис. 18 и сравнить приведенные конфигурации
поля с их обозначением. Указанная система
применима как к плоским, так и сферическим
зеркалам. Чем больше индексы 
и 
,
тем
более высоким считается тип колебаний.
Как уже отмечалось, каждой моде соответствует
определенное
затухание, зависящее от индексов моды
,
.
Это
означает, что добротность пассивного
оптического резонатора для различных
мод неодинакова (уменьшается с возрастанием
индексов тип, что будет показано ниже).
В случае лазерной ситуации это означает,
что в первую очередь должны возбуждаться
моды с наименьшими потерями. Поскольку
потери, связанные с коэффициентом
отражения зеркал, одинаковы для всех
мод, то очевидно, что различие
Рис. 18. Фотографии распределений полей в модах
в устойчивых резонаторах а) при цилиндрической
симметрии; б) при прямоугольной симметрии
в суммарных потерях связано с различиями в дифракционных потерях. Та мода, для которой они окажутся наименьшими, возбуждается раньше других. Дифракционные потери зависят от распределения амплитуды поля по поверхности зеркала.
Чем меньше амплитуда волны у края зеркала, тем
меньше
и дифракционные потери. Наименьшими
дифракционными потерями обладает мода
,
называемаяосновной
модой, затем
они возрастают по мере возрастания
индексов моды 
,
.
Угловая
расходимость излучения также увеличивается
с увеличением значений индексов мод,
растет и фазовый сдвиг
.
Моды резонатора, описываемые функциями (61), (62),
называются гауссовыми, а соответствующие им пучки излучения - гауссовыми пучками. Следует подчеркнуть, что гауссовы пучки могут самовоспроизводиться только в устойчивых (гауссовых) резонаторах, т.е. только устойчивые резонаторы способны формировать гауссовы пучки.
В неустойчивых резонаторах такие пучки не
самовоспроизводятся, т. е. не реализуются. Там реализуются сферические волны, т. е источник волн можно считать гомоцентричным.
Пучки, имеющие распределения поля, соответствующие
функции Гаусса (основная мода), функции Эрмита - Гаусса или Лагерра - Гаусса (моды более высоких порядков), а также в случае многомодового режима (одновременного присутствия нескольких поперечных мод) также называются гауссовыми, т. к. подчиняются одним и тем же законам распространения.