4. Основные явления, происходящие в оптическом резонаторе

Несмотря на простоту устройства, вернее, схемы

резонатора, в нем происходят довольно сложные процессы, связанные с распространением электромагнитных колебаний в ограниченном объеме и взаимодействием их с активным веществом. Для правильного понимания свойств резонатора необходимо учитывать, что в активном (т. е. заполненном активной средой) резонаторе источником энергии является инверсная среда, находящаяся внутри самого резонатора. Это, как будет показано ниже, приводит к тому, что распределение амплитуды и фазы поля на поверхности зеркал не является однородным. Однако, для простоты, начнем сначала рассматривать свойства резонаторов, исходя из теории, в которой предполагается наличие плоских однородных волн конечного размера, распространяющихся вдоль оси резонатора, а затем перейдем к более строгой теории.

Перечислим и поясним основные явления,

происходящие в активном резонаторе:

• усиление и потери мощности;

• формирование спектра излучения;

• "затягивание" резонансных частот;

• формирование модового состава излучения.

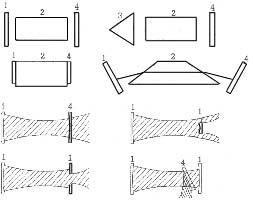
Рис. 3. Разновидности резонаторов и схемы вывода

излучения: 1 - глухое зеркало резонатора; 2 - активная

среда; 3 - призма полного внутреннего отражения;

4 - полупрозрачное зеркало

4. 1. Усиление и потери мощности. Пороговое условие генерации

Усиление распространяющегося внутри резонатора

излучения происходит при взаимодействии его с активным веществом, находящимся в инверсном состоянии, что было нами рассмотрено ранее [1].

Существенно, что одновременно с усилением в

активной среде происходят потери мощности. Применение резонатора увеличивает плотность мощности на частоте рабочего перехода, что повышает вероятность вынужденных переходов, но одновременно приводит к дополнительным потерям мощности. Чтобы генерация имела место, общие потери в резонаторе должны быть меньше, чем прирост мощности, получаемый при прохождении излучения через активную среду. Таким образом, потери определяют, во-первых, пороговое значение мощности накачки, которое должно быть достаточным, чтобы получить усиление, превосходящее потери; во-вторых, уровень излучаемой мощности во время генерации. При оценке величин усиления и потерь мощности удобно относить их к одному проходу излучения через резонатор (двойное прохождение длины резонатора, рис. 4). При этом будет учтена возможная асимметрия резонатора.

Рис. 4. Путь луча при одном проходе резонатора

Для возникновения генерации необходимо, чтобы

усиление превышало потери за один проход резонатора.

Прежде, чем более подробно написать это условие,

рассмотрим основные виды потерь:

- потери в активной среде за счет рассеяния на

неоднородностях и неактивного поглощения. Они оцениваются ранее введенным коэффициентом - показателем потерь []. Ослабление за счет этого фактора на пути может быть учтено как ;

- потери на зеркалах резонатора. Отражение от зеркала

сопровождается частичным рассеянием и поглощением излучения в зеркале и частичным прохождением через него. Рассеянное и поглощенное в зеркале, а также прошедшее через него излучения являются потерей для резонатора. Долю потерянной энергии при отражении от зеркал 1 и 2 можно, соответственно, оценить так: ();(), где - коэффициенты отражения соответствующего зеркала.

При отражении излучения от зеркала в результате

дифракции происходит распространение волны в пределах некоторого угла , который можно оценить по формуле , где - коэффициент, близкий к единице, зависящий от формы зеркал и распределения поля на них, - размер зеркала.

Вследствие конечных размеров зеркал часть энергии,

зависящая от утла и от амплитуды поля на краю зеркала, будет выходить за пределы резонатора и, следовательно, будет теряться при каждом отражении. Обозначим коэффициент дифракционных потерь через (безразмерная величина); он определяет часть энергии, которая теряется за счет дифракции за один проход резонатора;

- потери на торцах активной среды (когда активное

вещество твердое), или на оптических окнах, ограничивающих активную среду (жидкую или газообразную) - имеется в виду конструкция резонатора с внешними зеркалами.

Учет этих потерь особенно важен для газоразрядных

лазеров, в которых коэффициент усиления может быть малым. Здесь потери складываются из френелевских потерь, происходящих на поверхностях окон, а также возникающих вследствие неточной установки окон и потерь на поглощение в окнах. Обозначим коэффициент потерь на торцах (безразмерная величина) - доля энергии, теряемой на торцах за один проход резонатора.

Кроме указанных, существуют и другие виды потерь,

такие как потери из-за непараллельности зеркал, несовершенства их формы и т. п., однако здесь их рассматривать не будем.

Учитывая сказанное, можно записать следующее

условие возникновения генерации, считая для простоты, что протяженность активной среды равна :

, (1)

где - ненасыщенный показатель усиления активной среды, - исходная поверхностная плотность мощности.

Условие (1) означает, что интенсивность излучения с учетом всех процессов усиления и ослабления в резонаторе после одного прохода должна быть больше, чем до этого прохода. Это условие можно переписать так:

. (2)

Прологарифмировав выражение (2), нетрудно получить

следующую формулу условия самовозбуждения или генерации лазера:

. (3)

Как видно из этой формулы, чем больше коэффициент

отражения зеркал и длина активной среды, тем легче выполняются условия генерации. Однако одно из зеркал должно быть сделано частично прозрачным для вывода полезного излучения. Очевидно, что для получения максимальной мощности на выходе лазера существует оптимальное значение коэффициента пропускания "выходного" зеркала. Что касается длины, то она тоже не может быть слишком большой. В твердотельных лазерах ограничения возникают из-за технологических трудностей изготовления большой массы оптически однородной среды. Кроме того, с увеличением длины затрудняется условие накачки.

Если пренебречь дифракционными потерями и

потерями на торцах активной среды (что для ряда случаев правомерно) и считать , а, где- коэффициент отражения выходного зеркала, то выражение (3) можно упростить:

(4)

где называется коэффициентом полезных потерь.

Условие (4) можно записать и относительно

необходимой (пороговой) величины инверсии населенностей в активном веществе для возникновения генерации:

, (5)

где - скорость света в резонаторе, - скорость света в вакууме, - показатель преломления среды, заполняющей резонатор, - спектральный коэффициент Эйнштейна для вынужденного излучения, - центральная частота перехода.

Знание пороговой величины инверсии населенностей

позволяет, в свою очередь, рассчитать требуемую мощность источника накачки.

Сопоставляя выражения (4) и (5) с условием усиления

[1], можно сделать вывод, что при прочих равных условиях для получения эффекта генерации требуется более высокий уровень инверсии населенностей или значения , чем для получения эффекта усиления, что объясняется существованием дополнительных видов потерь в схеме лазера по отношению к схеме квантового усилителя. Вследствие этого же активная часть контура усиления, в пределах которой возможна генерация (), будет уже, чем та, в пределах которой может происходить усиление излучения () (рис. 5):

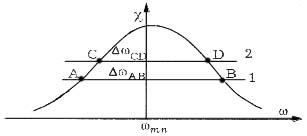
Рис, 5. Активная

Рис. 5. Активная часть контура усиления для усилителя

() и лазера (); 1 - уровень потерь усилителя; 2 - уровень потерь лазера

Выявив пороговое условие генерации, оценим теперь

мощность излучения, генерируемую активным веществом в резонаторе, а также мощность, выводимую за пределы резонатора и представляющую собой полезное лазерное излучение.

4. 1. 1. Оценка мощности излучения лазера. Мощность излучения, генерируемая активными центрами в единице объема, описывается выражением:

, (6)

где - поверхностная плотность мощности.

Учитывая, что

, (7)

и исключая из (6) и (7), получаем:

, (8)

где - параметр насыщения.

Обозначим через мощность излучения,

генерируемую во всем объеме активной среды лазера (считая, что физические величины не зависят от поперечных координат):

, (9)

где - площадь поперечного сечения активной среды; -длина резонатора (считаем, что активная среда полностью заполняет резонатор).

Подставляя (8) в (9), находим:

, (10)

где - коэффициент усиления, усредненный по длине резонатора.

Покажем это:

Поскольку в случае стационарной генерации

справедливо соотношение

, (11)

выражение (10) можно записать в виде:

. (12)

Отсюда, в частности, видно, что чем больше

разность, тем больше генерируемая мощность.

Из лазера выводится только часть генерируемой им

мощности, которая используется как лазерное излучение. Покажем, что существует оптимальная доля выводимой из оптического резонатора мощности, определяемая оптимальным коэффициентом полезных потерь, при котором выводимая мощность будет иметь максимальное значение.