5. Приближенные уравнения

ДЛЯ ОПИСАНИЯ ДИНАМИКИ ПРОЦЕССОВ

В ЛАЗЕРАХ (БАЛАНСНЫЕ УРАВНЕНИЯ)

Для описания взаимодействия оптического излучения с

веществом в квантовой электронике используют три основных метода: квантовомеханический, полуклассический и метод балансных уравнений.

Квантовомеханические методы предполагают квантовое

описание вещества и электромагнитного поля. В полуклассическом методе вещество описывают методами квантовой механики, а поле - классическими методами на основе уравнений Максвелла. Метод балансных уравнений исходит из квантовых представлений о веществе и поле, однако его исходные уравнения строятся на основе феноменологических, вероятностных положений о балансе числа частиц и фотонов.

Полуклассический метод является основным строгим

методом квантовой электроники, однако связан со значительными математическими трудностями.

Поэтому наибольшее распространение как в теории

лазеров, так и в практике их инженерных расчетов получил метод балансных уравнений, который мы и рассмотрим.

Система балансных уравнений позволяет найти

зависимость от времени для плотности инверсной населенности рабочих уровней и мощности генерируемого излучения, установить связь между выходной мощностью (или энергией импульса) и конструктивными параметрами лазера.

5. 1. Дифференциальное уравнение для плотности светового потока

В активной среде распространяются два потока

излучения вдоль оси в противоположных направлениях (рис. 24):

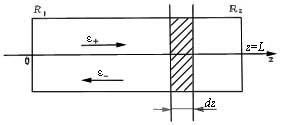
Рис. 24. Распространение потоков излучения в активной среде

Рассмотрим приращения потоков при их

распространении от точки до точки . Используя дифференциальный закон Бугера, запишем:

. (81)

Учтем, что процесс распространения потока от точки z

до точки требует времени . Таким образом,

, (82)

т.е. приращение плотности потока обусловлено двумя причинами' изменением плотности потока с расстоянием и изменением плотности потока во времени.

Выражение (82) можно записать через скорости

изменения потока с расстоянием и во времени, выразив их через производные и:

. (83)

Первое слагаемое отражает изменение

плотности потока с расстоянием, а второе - -изменение плотности потока во времени. Здесь учтено, что . Используя (83) перепишем уравнение (81) в виде:

. (84)

Поскольку , где σ - сечение перехода,

- плотность инверсной населенности рабочих уровней, уравнение (84) можно записать так:

. (85)

Аналогичное уравнение можно записать и для

плотности потока, распространяющегося в противоположном направлении:

. (86)

Уравнения (85) и (86) содержат три неизвестные

функции:

Перейдем к рассмотрению недостающего третьего

уравнения.

5. 2. Дифференциальное уравнение для плотности инверсной населенности

Рассмотрим в качестве примера трехуровневую схему,

изображенную на рис. 25.

Рис. 25. Трехуровневая схема

.

Здесь обозначено: - вероятность вынужденных

переходов в канале 1-3 под действием накачки; - вероятность вынужденных переходов в канале генерации 2-1; -вероятность спонтанных переходов в канале генерации;- вероятности спонтанных переходов в каналах 3-2 и 3-1, соответственно.

Балансные уравнения для заселенностей уровней

имеют вид:

(87)

Здесь полагаем, что . Тогда очевидно,

что . Вычитая первое уравнение из второго (87), находим:

. (88)

Далее воспользуемся двухуровневым упрощением:

будем полагать, что на уровне 3 активные центры практически не накапливаются (попадая на уровень 3, они быстро покидают его, переходя, в основном, на уровень 2). Это означает, что выполняется условие:

. (89)

При выполнении этих условий трехуровневая схема

становится похожей на двухуровневую:

. (90)

Используя (89), преобразуем третье уравнение (87) к

виду:

. (91)

Учитывая (90) и (89), перепишем (88):

. (92)

где

Учитывая, что , можно принять и,

следовательно,

В результате уравнение (92) принимает вид:

,

или окончательно:

. (93)

Обратимся теперь к схеме четырех уровней, где

оптическая накачка осуществляется в канале 1 - 4, а генерация - в канале 3-2. При этом будем, как и в случае трехуровневой схемы, использовать двухуровневое упрощение, в связи с чем будем полагать, что после попадания на уровень 4 активные центры быстро переходят на метастабильный уровень 3. Кроме того, будем полагать, что нижний уровень 2 быстро очищается (скорость перехода 2-1 велика).

В рамках такого упрощения нетрудно получить

следующее дифференциальное уравнение (в данном случае ):

, (94)

где и - вероятности вынужденных переходов в каналах генерации и накачки, соответственно; 1/ - вероятность спонтанных переходов в канале генерации.