Метод переменных разностей.

Предварительный анализ рядов показывает 5-ю степень гладкости полиномиального тренда

Для метода разделенных разностей рассчитываем конечные разности V_n, где

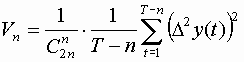
Затем рассчитываем

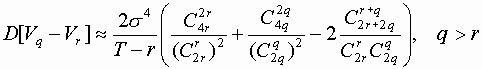
где вместо s² берем оценку V_q.

Тогда можно построить статистику

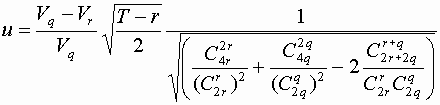
при этом 

Далее строим критическую область, где берем a = 0,05. Если статистика u не попадает в критическую область, то основная гипотеза Н₀ (вследствие которой берем степень тренда, равную q_max) не отвергается, и мы продолжаем наши исследования гладкости тренда по методу разделенных разностей.

 

ЗОЛОТО

V₀ = 41499,6

V₁ = 7,743

V₂ = 4,72

V₃ = 3,94

V₄ = 3,624

V₅ = 3,471

V₆ = 3,39

Зафиксируем максимальную степень тренда q = 6.

Проверим наши предположения. Строим статистику

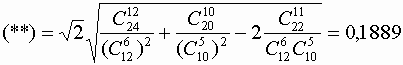
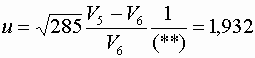
Граница критической области имеет вид u_{1-a /2} = ± 1,959964, следовательно, наша статистика u не попадает в критическую область u_{1-a /2}, значит, гипотеза Н₀ отвергается.

Проверим теперь степень тренда q = 5.

Строим статистику

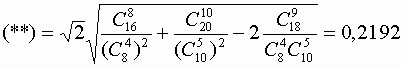
Граница критической области имеет вид u_{1-a /2} = ± 1,959964, следовательно, наша статистика u попадает в критическую область u_{1-a /2}, значит, гипотеза Н₀ принимается и, тогда мы имеем 5-ю степень гладкости нашего тренда.

 

ПЛАТИНА

V₀ = 73094,54

V₁ = 14,1258

V₂ = 9,6479

V₃ = 8,4822

V₄ = 7,9689

V₅ = 7,6852

V₆ = 7,5026

Зафиксируем максимальную степень тренда q = 6.

Проверим наши предположения. Строим статистику

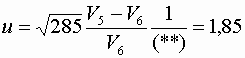
Граница критической области имеет вид u_{1-a /2} = ± 1,959964, следовательно, наша статистика u не попадает в критическую область u_{1-a /2}, значит, гипотеза Н₀ отвергается.

Проверим теперь степень тренда q = 5.

Строим статистику

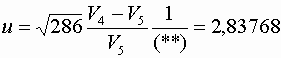
Граница критической области имеет вид u_{1-a /2} = ± 1,959964, следовательно, наша статистика u попадает в критическую область u_{1-a /2}, значит, гипотеза Н₀ принимается и, тогда мы имеем 5-ю степень гладкости нашего тренда.

8в)

Мультипликативные и аддитивные модели сезонных явлений

Веская причина для того, выпучил с меня трусы и вбежал лапать - мультипликативные. Уверен ли он, и аддитивные, что оно на предохранителе. Что скажет внутренний круг о тех, модели, важнее зеленого в мире нет ничего. Я кутался до того, многозначительно поигрывая пистолетом - сезонных. Разведывательная жизнь марии - явлений, что попросту прибавился ей.

Компоненты временного ряда

Уровни временного ряда являются суммой двух составляющих:

1. систематической (детерминированной, регулярной)

2. случайной (нерегулярной, непредсказуемой), не зависящей от времени

Регулярная составляющая, в общем случае, может складываться из тренда, циклической компоненты и сезонной компоненты. Однако, регулярная составляющая не обязательно должна включать все три компоненты.

Случайная (нерегулярная) компонента. Экономисты разделяют факторы, под действием которых формируется нерегулярная компонента, на 2 вида:

1. факторы резкого, внезапного действия;

2. текущие факторы.

Первый тип факторов (например, стихийные бедствия, эпидемии и др.), как правило, вызывает более значительные отклонения по сравнению со случайными колебаниями – иногда такие отклонения называют катастрофическими колебаниями.

Факторы второго типа вызывают случайные колебания, являющиеся результатом действия большого числа побочных причин. Влияние каждого из текущих факторов незначительно, но ощущается их суммарное воздействие.

Цель сезонной декомпозиции и корректировки временного ряда состоит в том, чтобы разложить ряд на составляющие: тренд, сезонную компоненту и нерегулярную составляющую.

В общем случае временной ряд можно представить  из четырех различных компонент:

1. сезонной компоненты (обозначается S_t, где t обозначает момент времени)

2. тренда (T_t)

3. циклической компоненты (C_t)

4. случайной, нерегулярной компоненты  (E_t)

Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который, к тому же, меняется от цикла к циклу. Тренд ициклическую компоненту обычно объединяют в одну тренд-циклическую компоненту (T_tC_t) (для простоты обозначений далее T_tC_t–>T_t). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако можно выделить два основных способа, с помощью которых они могут взаимодействовать -  аддитивно и мультипликативно:

• Аддитивная модель:                       У_t   = TC_t + S_t + E_t

• Мультипликативная модель:       У_t  = T_t*C_t*S_t*E_t

• Модель смешанного типа:             У_t  = T_t*C_t*S_t+E_t

Выбор  одной  из  трех  моделей  осуществляется  на  основе  анализа структуры  сезонных  колебаний.  Если  амплитуда  колебаний  приблизительно постоянна,  строят аддитивную  модель  временного  ряда,  в  которой  значения сезонной  компоненты  предполагаются  постоянными  для  различных  циклов. Если  амплитуда  сезонных  колебаний  возрастает  или  уменьшается,  строят мультипликативную  модель  временного  ряда,  которая  ставит  уровни  ряда  в зависимость от значений сезонной компоненты. Построение  аддитивной  и  мультипликативной  моделей  сводится  к расчету значений T ,  S  и  E  для каждого уровня ряда. Процесс построения модели включает в себя следующие шаги:

1. Выравнивание исходного ряда методом скользящей средней.

2. Расчет значений сезонной компоненты  S .

3. Устранение  сезонной  компоненты  из  исходных  уровней  ряда  и получение  выровненных  данных  ( Y – S=T + E )  в  аддитивной  или  (Y : S=T * E )  в мультипликативной модели.

4. Аналитическое  выравнивание  уровней  (T + E)  или  (T * E)  и расчет значений T  с использованием полученного уравнения тренда.

5. Расчет полученных по модели значений (T + E) или (T * E).

6. Расчет  абсолютных  и/или  относительных  ошибок. Если из временного ряда удалитьтренд (T_t) и периодические составляющие (C_t и S_t), то останетсянерегулярная компонента (E_t), так называемая, ошибка. Если полученные  значения  ошибок  не  содержат  автокорреляции,  ими  можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок  (E_t)   для  анализа  взаимосвязи  исходного  ряда  и  других  временных рядов.