49

Обслуживание синхронных компенсаторов

2.1. Реактивная мощность

Нагрузка электрической системы наряду с активной всегда содержит реактивную составляющую. Под нагрузкой здесь понимается мощность, необходимая потребляющей части системы в некоторый рассматриваемый момент времени. Таким образом, нагрузка -это активная и реактивная мощности, потребность в которых удовлетворяется генерирующей частью системы.

Активная.мощность представляет собой энергию, которая потребляется цепью переменного тока за единицу времени. Она выражается произведением действующих значений напряжения I/, силы тока / и фазового сдвига между этими величинами, на угол  т.е. Р =U×I×cos

Умножение активной мощности на время дает электрическую энергию, которая с помощью физических эквивалентов может быть выражена в других видах энергии (тепловой, механической и др.).

Активная мощность получается в результате преобразования первичных видов энергии (например, сжигания топлива на электростанциях). Потоки активной мощности всегда направлены от генераторов электростанций в сеть.

Реактивная мощность необходима потребителям электрической энергии, которые по принципу своего действия используют энергию магнитного поля. Потребителями реактивной мощности являются асинхронные двигатели, индукционные печи, люминесцентное освещение, трансформаторы для дуговой сварки, а также отдельные звенья передачи электрической энергии — трансформаторы, реакторы, линии и др.

Формула реактивной мощности Q=U×I×sin по своей структуре идентична формуле активной мощности Р =U×I×cos.- Мало того, в выражении полной мощности S = оба эти компонента равноценны. Однако физически Р и Q существенно различны, и сходство между ними формальное.

Активная мощность является результатом перемножения периодических синусоидальных величин U и I_а=I×cos совпадающих по фазе, а реактивная мощность — результатом такого же перемножения величин U и I_p=I×sin, сдвинутых по фазе на угол 90° (рис. 2.1).

В первом случае перемножаются величины одного знака и синусоида мгновенных значений мощности р расположена выше оси абсцисс (рис. 2.2.а), при этом мощность является определённой существенно положительной величиной. Во втором случае перемножаются величины как одного знака, так и разных знаков, а полупериоды результирующей синусоиды мгновенных значений мощности, имею

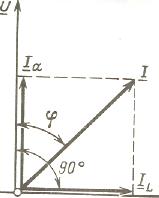
Рис .2.1.

Разложение полного тока на активную и реактивную составляющие

щей удвоенную частоту, располагаются попеременно то выше, то ниже оси абсцисс так, что среднее значение мощности р за любой интервал времени, кратный полупериоду частоты равно нулю (рис. 2.2, б).

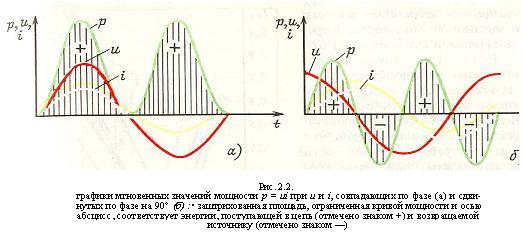К оличество магнитной энергии, периодически запасаемой индуктивностью, связано с характером изменения синусоидального тока. Она то накапливается в индуктивности до некоторого максимального значения, то убывает до нуля. За один период переменного тока магнитная энергия дважды поступает от генератора в цепь и дважды он получает ее обратно, т.е. реактивная мощность является энергией, которой обмениваются генератор и потребитель. Она не имеет никакого физического эквивалента для перевода в другие виды энергии. Физический смысл реактивной мощности сводится лишь к скорости изменения энергии магнитного поля, что необходимо, например, и при передаче энергии из одной обмотки трансформатора в другую, и при работе электродвигателя с механической нагрузкой на валу, где энергия статора электродвигателя передается ротору также с помощью переменного магнитного поля.

Для получения реактивной мощности не требуется непосредственных затрат первичной энергии (топливо на электростанциях не расходуется). Однако при обмене энергией между генератором и потребителем и обратно в обмотках генератора и в сети возникают дополнительные потери активной мощности, требующие затрат первичной энергии. Так, например, потери в линии при передаче реактивной мощности в простейшей цепи однофазного синусоидального тока составят ∆Р_а=( I×sin)²×R, где R -активное сопротивление линии.

Таким образом, передача реактивной мощности к месту ее потребления сопряжена с активными потерями во всех звеньях передачи, которые должны покрываться активной энергией генераторов. Поэтому возникает проблема возможного снижения этих потерь.

В теории переменных токов рассматривают два вида реактивной мощности: реактивную мощность при отстающем от напряжения векторе полного тока генератора и реактивную мощность при векторе полного тока, опережающем вектор напряжения. Считают, что эти два вида реактивной мощности противоположны по направлению (по знаку) и при их совместном рассмотрении они компенсируют ("уничтожают") друг друга, при этом сеть разгружается от реактивной мощности. В нагрузке электрических систем отстающая (индуктивная) составляющая реактивной мощности, как правило, преобладает над опережающей (емкостной) составляющей реактивной мощности. Поэтому от генераторов электростанций требуют генерирования активной мощности и реактивной отстающей мощности, именно той реактивной мощности, которая требуется нагрузке. Для этого генераторы рассчитывают на работу с коэффициентом мощности cos <1, что позволяет им выдавать в сеть значительную реактивную мощность и обеспечивать ее регулирование.

Получение реактивной мощности связано исключительно с уровнем возбуждения синхронной машины. Увеличение тока возбуждения приводит к увеличению генерирования реактивной мощности (при этом топливо дополнительно не расходуется). Снижение тока возбуждения приводит к противоположному результату.

Помимо синхронных генераторов источниками генерирования реактивной мощности в электрических системах являются емкостные их элементы -статические конденсаторы, линии электропередачи (особенно линии электропередачи высших классов напряжения), относительно перевозбужденные синхронные двигатели, синхронные компенсаторы и т.д., работающие параллельно с генераторами электростанций