7) 8) Тепловой расчет трансформатора питания:

Из формулы (3) (см. вопрос 3) следует, что температура перегрева трансформатора равна:

.

Вычислим математическое ожидание температуры перегрева, используя предыдущее выражение:

. (*)

Для осуществления вероятностного расчета необходимо также дать вероятностное описание коэффициентов А и Б, входящих в выше написанную формулу. Значения этих коэффициентов в общем случае случайны и определяются геометрическими размерами трансформатора, состоянием его поверхности, условиями циркуляции воздуха, атмосферным давлением и т. д. Однако, если осуществить анализ для оценки свойств трансформаторов определенной конструкции, то следует считать условия охлаждения одинаковыми и идеализированными. Тогда, в первом приближении, можно считать, что случайные величины А и Б имеют относительно небольшие отклонения значений по сравнению с теми, которые имеют и . В этих условиях А и Б можно считать детерминированными величинами и рассчитывать по формулам (2) (см. вопрос 3).

Значение среднеквадратического отклонения температуры перегрева, , в общем случае рассчитывается из соотношения:

, где n – число первичных параметров ; - среднеквадратическое отклонение первичного параметра ; - коэффициент влияния для отклонения параметра.

Коэффициенты влияния и для отклонения первичных параметров и рассчитываются по следующим формулам:

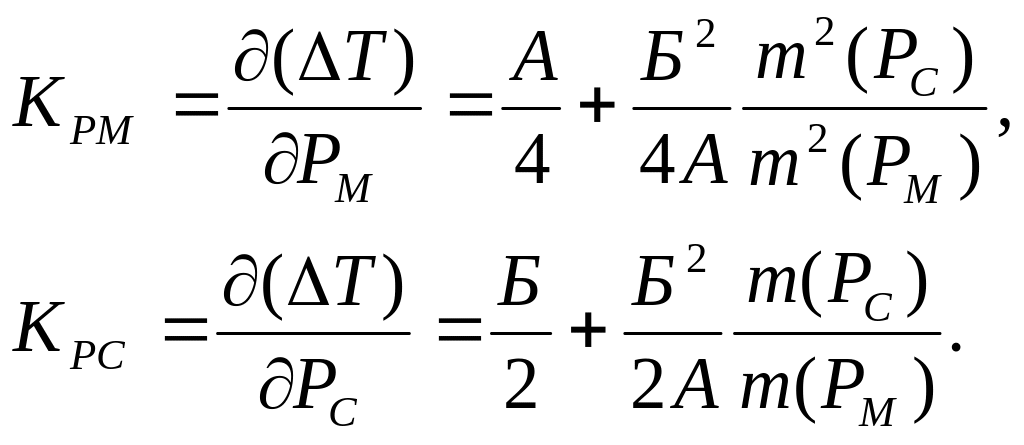
С учетом данных выражений, выражение для приобретает вид:

. (**)

Последние выражения есть определения значений математического ожидания и среднеквадратического отклонения температуры перегрева трансформатора (статический анализ).

Перейдем к расчету вероятностных характеристик первичных параметров, входящих в данные формулы.

Числовые характеристики потерь в стали определяются следующими выражениями:

, где - удельные потери на 1 кг магнитопровода, Вт/кг; - масса магнитопровода, кг. Значение удельных потерь в магнитопроводе регламентируется ГОСТами для соответствующих марок трансформаторной стали. Величина потерь зависит от величины индукции B в магнитопроводе, частоты тока f и толщины стального листа δ.

Расчет тепловых потерь в меди более сложен. Потери в проводах обмоток трансформатора определяются по формуле:

, где (4)

- число обмоток трансформатора;

- значение тока в i-ой обмотке;

- случайное значение сопротивления i-ой обмотки трансформатора с учетом перегрева.

Величину математического ожидания и среднеквадратического отклонения потерь в меди можно рассчитать из соотношений:

(5)

(6)

В данных соотношениях токи обмотки рассчитываются детерминированными величинами, равными их номинальным значениям. Это существенно облегчает расчёт. Величина тока i-ой вторичной обмотки при заданном вторичном напряжении определяется номинальным значением нагрузки :

.

Для получения номинального значения необходимо учесть дополнительный ток в первичной обмотке, обусловленный потерями в меди всех обмоток трансформатора и потерями в магнитопроводе. Из формулы следует, что величина активной составляющей тока первичной обмотки равна:

. (7)

Трудность расчёта данного выражения состоит в том, что необходимо заранее знать величину потерь в меди , которую, собственно, и необходимо определить. Поэтому рассчитывают предварительное значение в предположении, что ток первичной обмотки, входящий в соотношение для потерь в меди, обусловлен только нагрузкой. Тогда соотношение (4) приобретает вид:

.

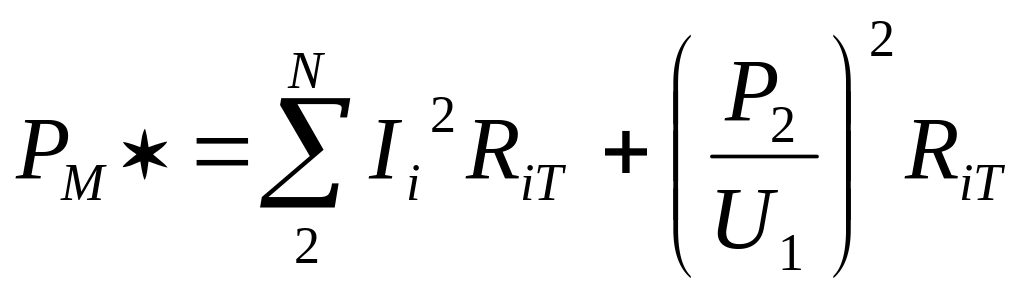Подставляя значения (7) и в формулу для тока , получим, что:

.

Для выполнения вероятностного описания сопротивления обмоточных проводов, , в соотношениях (6) и (7) предварительно рассчитываются номинальные значения сопротивлений обмоток при Т = 20^о С по формуле:

, где

- общая номинальная длина провода намотки, м;

- номинальное сечение провода, мм².

Отклонение величины определяется отклонением размеров проводов в состоянии поставки, геометрических размеров обмотки и диаметра провода из-за растяжения при намотке, а также влиянием случайной температуры перегрева . Поэтому необходимо рассчитать величину математического ожидания и среднеквадратического отклонения сопротивления провода i-ой обмотки по формулам:

,

,

где

- относительное отклонение среднего значения сопротивления единицы длины провода от номинального;

- относительное среднеквадратическое отклонение сопротивления единицы длины провода.

Величина математического ожидания сопротивления обмоток с учётом перегрева определяется по формуле:

где

- математическое ожидание температуры перегрева трансформатора;

- случайная величина температуры нагрева трансформатора обусловленная температурой окружающей среды, температурами перегрева блока и трансформатора;

Т = 20^о С;

- температурный коэффициент сопротивления меди.

Среднее квадратическое отклонение сопротивления провода от номинального рассчитывается из выражения:

,

где

- среднеквадратическое отклонение температуры перегрева трансформатора относительно температуры блока РЭА, в котором он установлен.

Коэффициенты А и Б рассчитываются по формулам (2), предварительно определив размеры магнитопровода и элементов конструкции трансформатора.

Использование выражений (*) и (**) позволяет для каждого конкретного случая выполнить расчёт числовых характеристик температуры перегрева трансформатора . Если принять гипотезу о близости закона распределения к нормальному, то можно построить функцию распределения , и определить вероятность того, что по перегреву трансформаторы будут находиться в определённых границах, то есть будут годными, если по требованиям к надёжности или по другим причинам температура перегрева ограничена.