20)Метод избыточных величин Гиббса

М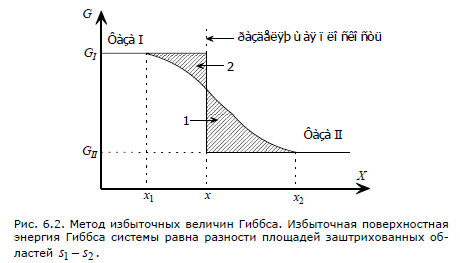 етод избыточных величин Гиббса. По этому методу принимается, что поверхностный слой – это неоднородный тонкий слой, разделяющий объемные фазы и обладающий конечной толщиной и объемом, а объемные фазы рассматриваются как однородные вплоть до границы раздела. Такая система отличается от реальной тем, что в ней свойства системы в области поверхности раздела изменяются скачкообразно, тогда как в реальной системе наблюдается некоторая сглаженность перехода от одной фазы к другой. В качестве параметра, характеризующего свойство поверхностного слоя, рассматривают разность свойств такой идеализированной и реальной систем, называемую избыточной термодинамической величиной; при отнесении ее к площади поверхности раздела получают удельную поверхностную величину. Например, энергия Гиббса двухфазной системы, изображенной на рис. 6.2 равна сумме энергий Гиббса однородных объемных фаз (G1 и G2 ) и энергии Гиббса поверхностного слоя, расположенного между точками х1 и х2. В идеализированной системе фазы будут однородными вплоть до разделяющей плоскости, проходящей через точку х. Избыточная поверхностная энергия Гиббса системы определяется разностью откуда следует, что поверхностное натяжение является удельной поверхностной энергией Гиббса. Очевидно, что значение избыточной величины зависит от положения поверхности раздела, например при проведении разделяющей плоскости через точку х1 избыточная поверхностная величина будет положительной, через точку х2 отрицательной. Это вносит определенные трудности при использовании данного метода.

21)Капиллярное давление (определение, физический смысл, от чего зависит?)

Капиллярное явление наблюдается в сосудах, содержащих жидкость у которых расстояние между стенками соизмеримо с радиусом кривизны пов-ти жидкости.

Поведение ж-ти в капиллярных сосудах зависит от того, смачивает или нет жидкость стенки сосуда. При смачивании наблюдается поднятие уровня в капилляре за счет растяжения ж-ти, а при не смачивании наоборот- опускание в рез-те сжатия. При равновесии Лапласовское давление = гидростатическому

Где ρ - плотность жидкости

ρ₀ - плотность газовой фазы

g- ускорение свободного падения

r-радиус мениска

h - высота столба

Пример: Капиллярное впитывание играет существенную роль в водоснабжении растений, передвижении влаги в почвах и др. пористых телах. Капиллярная пропитка различных материалов широко применяется в процессах химической технологии.

дисперсные частицы с выпуклой поверхностью-капля жидкости в аэрозоле или эмульсии.выпуклая поверхность имеет мениск несмачиваемой жидкости в капилляре.

вогутая поверхность-мениск смачиваемой жидкости в капилляре

22)Закон Лапласа

Вследствие избыточной поверхностной энергии подвешенная жидкость в условии невесомости приобретает сферическую форму. С уменьшением кол-ва жидкости роль силы тяжести снижается, т.к. она уменьшается пропорционально кубу, а поверхность квадрату радиуса тела, т.е. увеличивается удельная поверхность . С появлением кривизны пов-ти тела радиусом r возникает дополнительное внутреннее давление дельта Р Его можно представить как равнодейств. силу пов-го натяжения ,сходящихся в одной точке. Равнодейсв. направлена перпендикулярно пов-ти в центр кривизны.

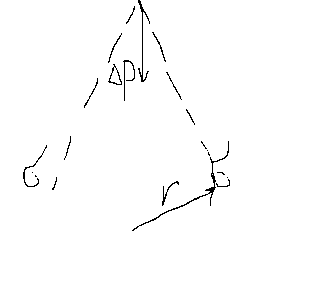
Эта сила рассчитана на ед площади и представляет собой доп-е давление:

Где Δ Р - разность давлений внутри тела с изогнутой и плоской пов-ти. кривизна поверхности. Чем больше σ, тем влияние кривизны значительное для сферической формы.

Для цилиндрической пов-ти длиной L и радиусом r имеем:

Тогда:

для пов-ти неправильной формы используется представление средней кривизны, опред. по уравнению:

Где 1/r₁ и 1/r₂ -кривизна главных нормальных сечений 1 и 2.

Тогда:

- это и есть уравнение Лапласа.