Вариационные задачи на условный функционала

Задачи на условный экстремум функционала – это задачи вариационного исчисления, когда кривые , на которых задан функционал, помимо граничных условий должны удовлетворять некоторым другим условиям, например уравнениям связи или уравнениям объекта (1). Таким образом, пятая типовая задача управления есть частный случай задачи на условный функционала, правда в последней принято уравнение связи (1) представить с нулевой правой частью

или

вводя абстрактную математическую переменную , по физическому, включающую в себя и вектор состояния и вектор управления , ограничения

или в скалярной форме

Тогда 5 типовая задача управления с абстрактной математической переменной будет выглядеть следующим образом:

Определить функционала

,

при нем допустимые кривые удовлетворяют граничным условиям

и условиям

Уравнение связи (15) полагаются независимыми, т.е. ранг функций матрицы

вдоль кривой доставляющей , для всех значений .

Таким образом, функционал (16) рассматривается не на всех допустимых кривых, удовлетворяющих граничным условиям (17), а только на тех кривых, которые удовлетворяют системе уравнений (15). Отметим, что граничные условия (17) и уравнения связи (15) должны быть согласованы, т.е. начальная и конечная точки должны принадлежать мерному многообразию, которое задается системой равенств (15).

Изучая пятую типичную задачу, мы рассматриваем в качестве уравнений связи (15) дифференциальные уравнения. В общем случае в вариационной задаче на условный экстремум функционала в качестве уравнения связи могут быть использованы алгебраические

и интегрированные соответствия

Если уравнения связи (15) являются дифференциалом (15), то имеет место общая задача Лагранжа. В случае (19) получается геодезическая задача или задача Лагранжа со сложными связями. Задачу при ограничениях, в форме интегральных соотношений (20) называют изотермической. Из всех 3-х более полной является общая задача Лагранжа, которую мы будем в дальнейшем рассматривать, а остальные могут быть получены, как частный случай задачи Лагранжа.

Общая задача Лагранжа решается аналогично задаче на условный функции с использованием метода неопределенных множителей Лагранжа, который мы изложим без доказательства.

Введем в рассмотрение новый функционал.

, причем

где - неопределенные пока (на момент постановки задачи) множители Лагранжа.

- левые части уравнений связи (15) с нулевыми правами частями.

Подынтегральная функция (22) для геодезической задачи выглядит так

, а для изопериметрической

,

причем , а и в двух последних соотношениях берутся из выражения (19) и (20).

Отметим, что в формуле (21) неизвестными являются и т.е. всего переменных. Найдем безусловный этого функционала по всем переменным.

Для этого составим уравнения Эйлера-Лагранжа:

или с учетом (22) уравнение (6) примет вид

Эта система уравнений содержит неизвестных с произвольными постоянными, для определения которых используются граничные условия (17). Таким образом, система уравнений (23) позволяет найти неизвестные пока множители Лагранжа. и , доставляющий безусловный функционала (21) и одновременно условный функционала (16) при наличии уравнений связи или [(19) и (20) для геодезической изотермической задач].

Пример.

уравнение связи объекта, инерционное звено

___________________

Конструируем вспомогательную функцию

Уравнение Эйлера-Лагранжа для этого функционала.

Тогда

Отсюда следует

Отсюда характеристический определитель

подставим в

Результат решения задачи отображен на рисунка 1 и 2.

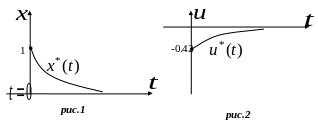
Найденное значение и позволяют осуществлять управление только по разомкнутому циклу

Алгоритм функционирования УУ можно получить и по замкнутому циклу.

регулятор

Если на и накладываются ограничения, то они становятся негладкими и решение будет сложным.