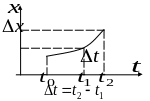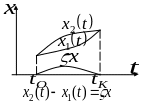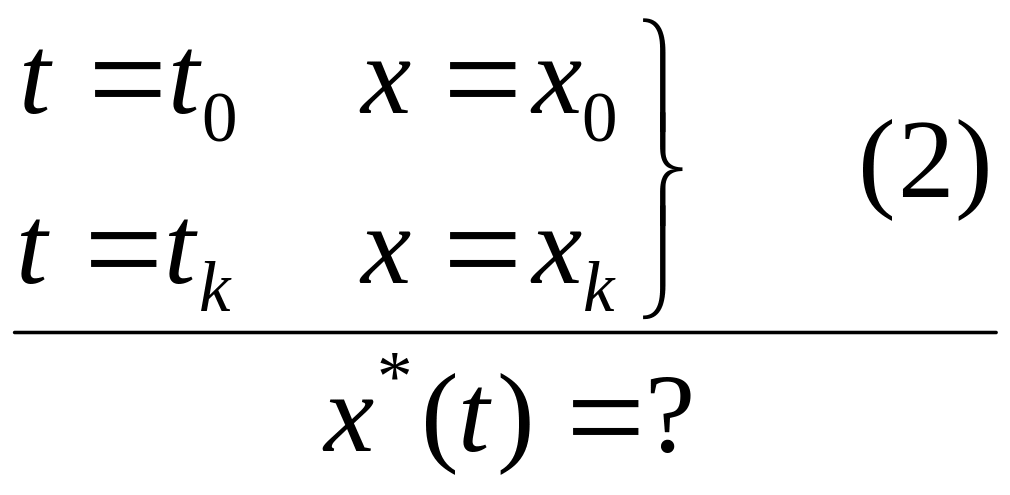Свойство функционала

	Свойство функции	Свойство функционала
	, где Значение функции	есть функционал от функции заданного класса, если каждой функции этого класса соответствует некоторое число. -число, зависящие от вида функции.
	График функции	Г рафик функционала Каждая точка оси изображает некоторую функцию
	Приращение аргумента функции	Приращение аргумента функционала
	Непрерывные функции Малому приращению аргумента соответствует малое приращение функции	Непрерывность функционала Если и близки друг к другу… В функционал могут входить не только переменные , но и их производные. При этом может получиться что и будут близки друг к другу, но сильно различаться по производной, поэтому вводят понятие близости 0,1,2 и т.д. порядков.
	Линейность функции Функция линейна, если она аддитивна и однородна. Аддитивность Однородность	Линейность функционала 5.1 Аддитивность 5.2 Однородность
	Приращение функции и дифференциал	Приращение функционала дифференциал Линейная часть приращения называется вариацией
	Экстремум функции	Экстремум функционала Необходимым условием экстремума функции является равенство линейной части приращения функционала.

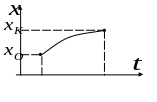
Безусловный экстремум функционала Простейшая задача вариационного исследования

Вариационное исследование – раздел математики решающий задачи определения наименьшего и наибольшего значений функционала, а так же определения наименьших и наибольших значений функционала, а также определения кривых, на которых достигается функционала.

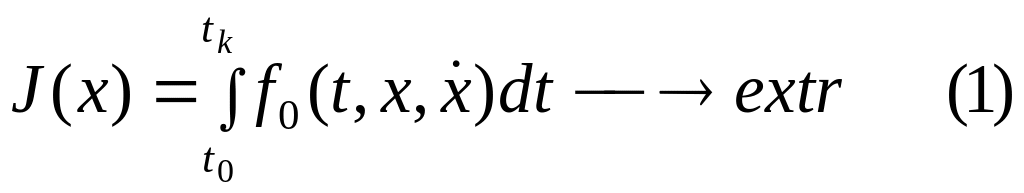
Частный случай функционала для одной переменной

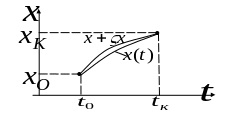
Искомые координаты заданы, с закрепленными концами. Функции гладкие. - оптимальная кривая, доставляющая функционала (1)

Придадим этой кривой вариацию .

Отметим ограничения.

1. Кривые и 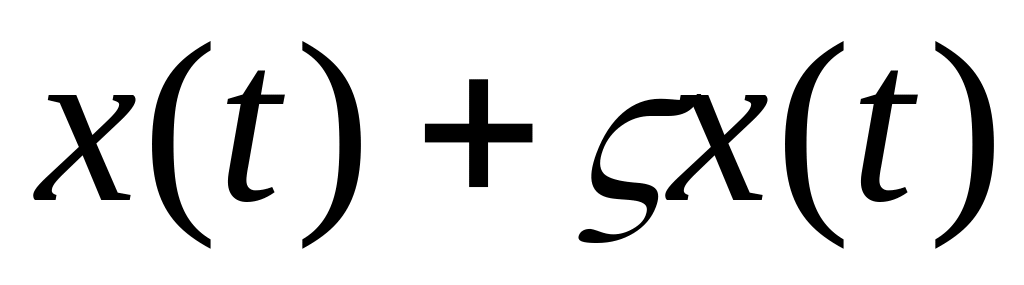должны быть близки по первому порядку.

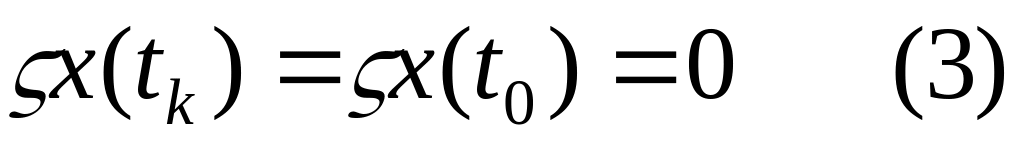2. т.е. вариации в граничных точках нулевые.

Запишем приращение функционала.

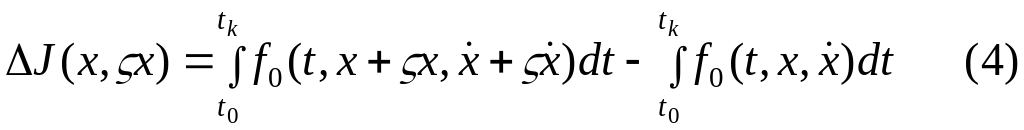
Возьмем подынтегральную функцию первого интеграла и разложим её в ряд Тейлора по вариациям и .

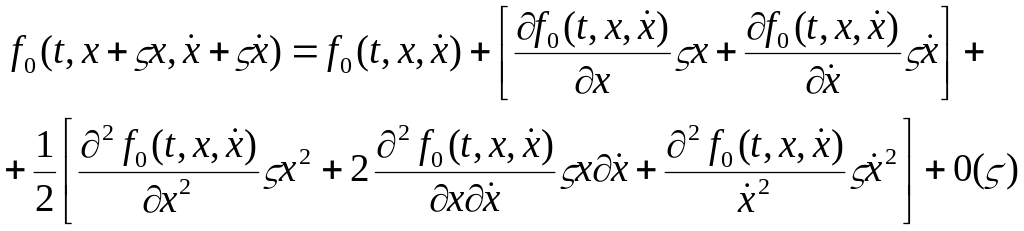
Подставим это выражение в (4), получим:

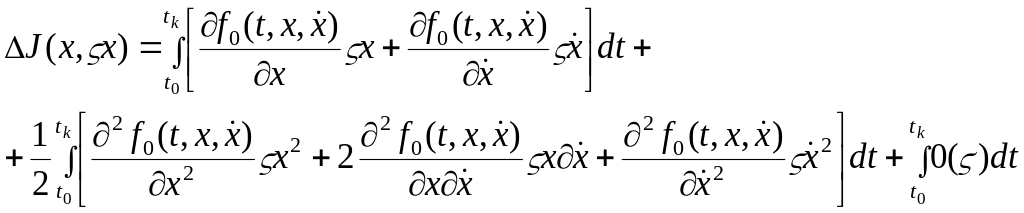
Первый интеграл в правой части этого выравнивания есть линейная часть приращения функционала, т.е. его первая вариация , второй интеграл – это вторая вариация функционала , а третий интеграл получается из последующих членов разложения.

Мы раньше выяснили, что первым необходимым условием функционала является равенство нулю его первой вариации.

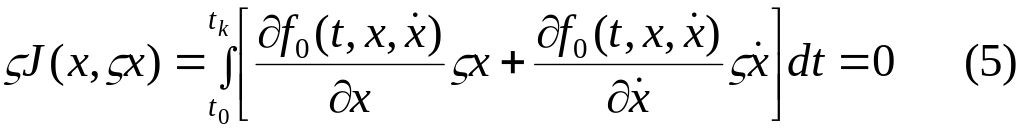
Для решения этого интегрального уравнения второе слагаемое подынтегрального выражения в правой части проинтегрируем по частям.

Обозначим

Поскольку

, то

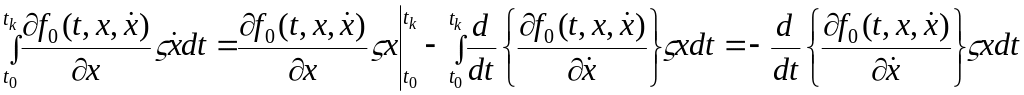поскольку первое слагаемое тождественно равно нулю в силу

Следовательно, выражение (5) предстанет в виде:

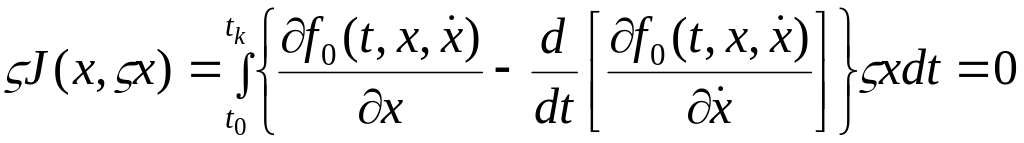
При произвольном , если будет равно нулю

Это уравнение называется уравнение Эйлера решением которого является экстремаль , т.е. функция, доставляющая экстремум функционалу. Следует отметить, что уравнение Эйлера не всегда разрешимо, однако для многих важных практических случаев теории управления решение можно найти. Как нетрудно видеть, уравнение Эйлера представляет собой обыкновенное дифференциальное уравнение второго порядка. Общие решение такого уравнения содержит две произвольные постоянные, которые в общем случае могут быть определены с учетом граничных условий (2).

Для того чтобы определить или имеет функционал необходимо найти

(7) , а если то .

Это так называемое условие Лагранжа.

Пример.

Найти экстремаль , соответствующую функционалу

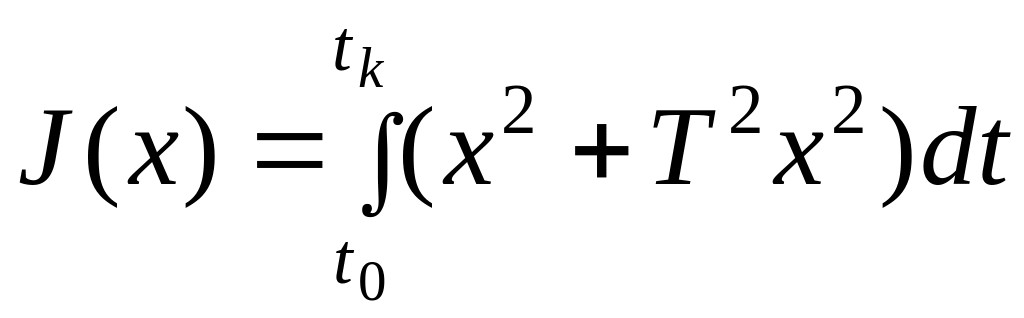при

Поскольку , то уравнение (6) Эйлера для данной задачи имеет вид:

или

, а при

=0. Этому дифференциалу уравнению соответствует характерное уравнение

с корнями .

Тогда общее решение дифференциального уравнения, т.е. поле экстремалей.

Заданным граничным условиям соответствуют нужные и и искомая экстремаль .

Откуда

Условие Лежандра т.е. имеет место минимум функционала.

В приложениях часто встречается задача с несобственным интегралом, например

Уравнение экстремалей для него остается прежним

, а постоянные интегрирования и определяются теперь из условий при и . При движение должно быть устойчивым т.е. при . Это может быть только в том случае, когда . Следовательно, уравнение экстремали будет иметь вид . Постоянная определяется из начального условия ; и искомая экстремаль будет

Рассматривая простейшую вариационную задачу, мы имеем дело с функционалом, экстремум которого зависит от скалярной функции . Получим необходимые условия экстремума функционала для общего случая.

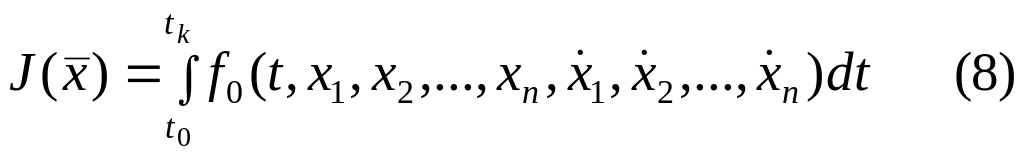
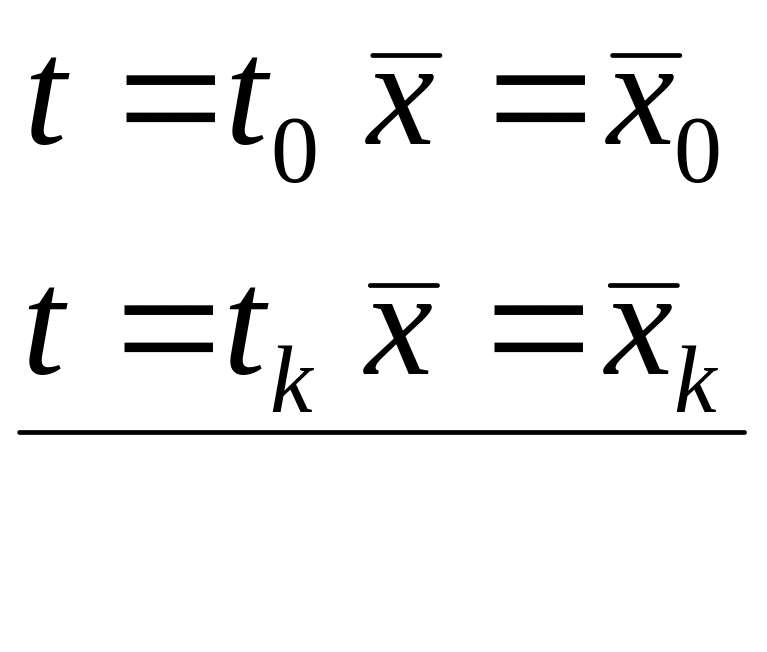
Данный функционал зависит от «n» функций . Здесь -чисто математическая величина, которая с точки зрения физики явление может включать в себя и вектор состояния и вектор управления функционала (2).

Получаем, что функция

и удовлетворяет граничным условиям

Подход решения такой:

1.Фиксируем все переменные кроме первой . Затем проводим, т.е. же манипуляции и с другими переменными.

2. Фиксируем все переменные кроме второй. Получаем простейшую задачу относительно .

3. И т.д. до самой последней переменной

Решением уравнения будут экстремали

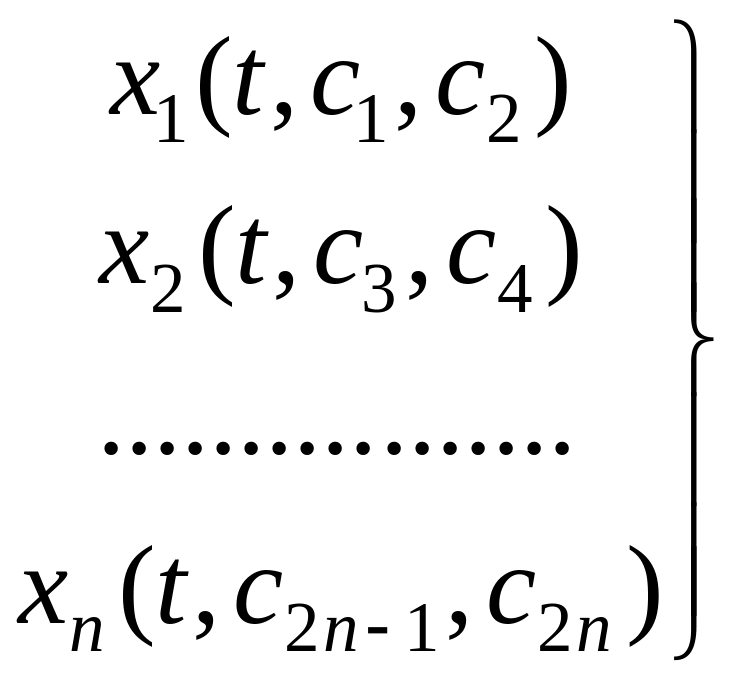Которые находим из граничных условий.

Для определения или функционала, необходимо рассматреть условие:

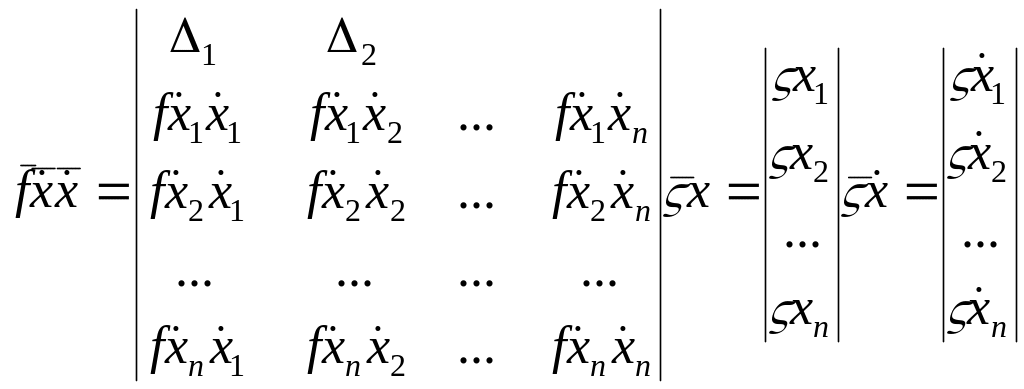
Простейшая вариационная задача легко обобщается на случай, когда подынтегральная функция содержит производные высших порядков и функционал имеет вид.

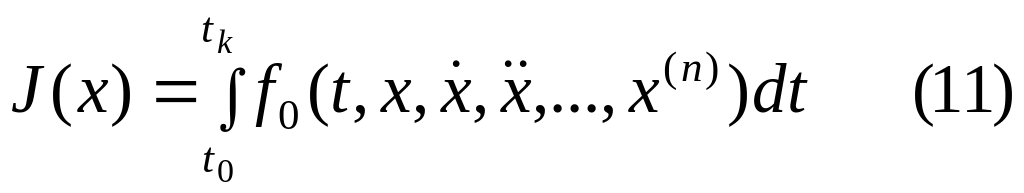
Экстремум определяется на класс кривых , удовлетворяющих граничным условиям

Методика получения первого необходимого условия экстремальной функции остается прежней: находится 1-ая вариация функционала и приравнивается нулю, что после ряда преобразований приводит к уравнению

,

которое называется уравнением Эйлера-Пуассона и представляет в общем случае нелинейное дифференциальное уравнение -ого порядка. Его решение . Содержит постоянного интегрирования, которые находят на основании такого же количества заданных граничных условий.

Условие Лежандра в данной задаче следующие: для достижения минимума на некоторой экстремали необходимо выполнение неравенства

, а для максимума

Пример.

Найти экстремаль функционала

при граничных условиях

В рассматриваемом случае

, т.е.

Уравнение Эйлера-Пуассона имеет вид

, т.е.

Отсюда:

Найдем постоянные интегрирования.

Отсюда ;

И экстремаль будет

Условие Лежандра здесь

и предполагает, что на данной экстремали достигается максимум.