Критерий оптимальности
Выше уже говорилось, что в теории оптимального управления в качестве критериев оптимальности, как правило, применяются интегральные функционалы вида (2). В зависимости от вида подынтегральной функции могут быть получены различные критерии оптимизации, применяемые в практике проектирования оптимальных САУ.
Одним из наиболее распространенных
критериев, для которого методика синтеза
оптимального управления достаточно
хорошо разработана, является время
переходного процесса объекта управления
из начального состояния
в конечное
.
Этот критерий представляет собой частный
случай функционала (2) при
тогда
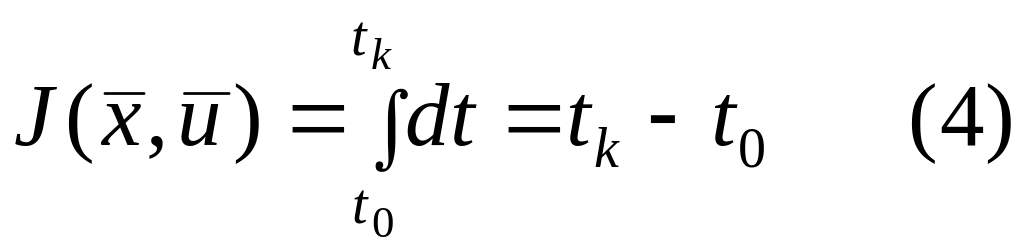
Казалось бы логично пользоваться интегральным критерием вида
,
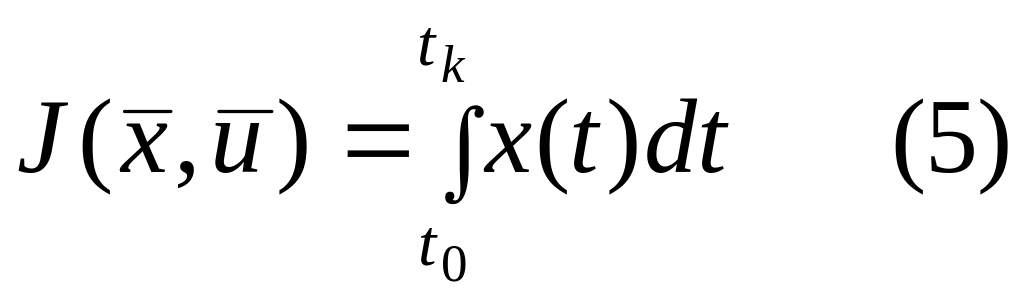где
-
отклонения регулируемой координаты от
нового установившегося значения, которое
она будут иметь после завершения
переходного процесса.
Геометрически интеграл (5) интегрируется
как площадь под кривой
.
Эта площадь, а, следовательно, и величина
критерия оптимальности, будет тем
меньше, чем быстрее затухает переходной
процесс и чем меньше величина отклонения
в совокупности. Значит управление
системой
надо
выбирать так, что минимизировать критерий
(5). Неудобством этой интегральной оценки
является то, что она годится только для
монотонных процессов, когда не меняется
.
Если же имеет место колебательный
процесс рис.5, то при вычислении интеграла
(5) площади будут складываться алгебраически
и минимум этого интеграла может
соответствовать колебаниям с малым
затуханием или вообще без затухания.
Что избежать риски подобных ситуаций,
следует использовать квадратичный,
интегральный функционал
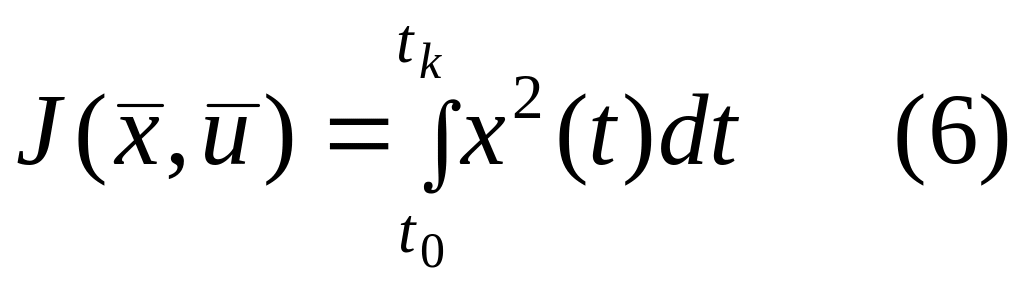
который не зависит от знаков отклонений, а значит и от формы переходного процесса (монотонный или колебательный).
Если при проектировании системы оптимального управления ставится задача ограничить резкие изменения выходной переменной во время изменения переходного процесса, при которых 1-ая производная может принимать достаточно большие значения, используется функция:
,
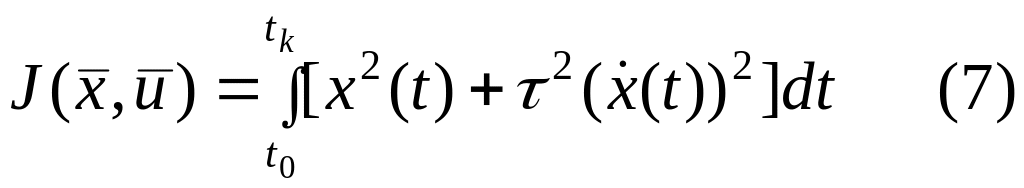где
- весовой коэффициент.
Минимизация этой формулы означает, что
составляющая
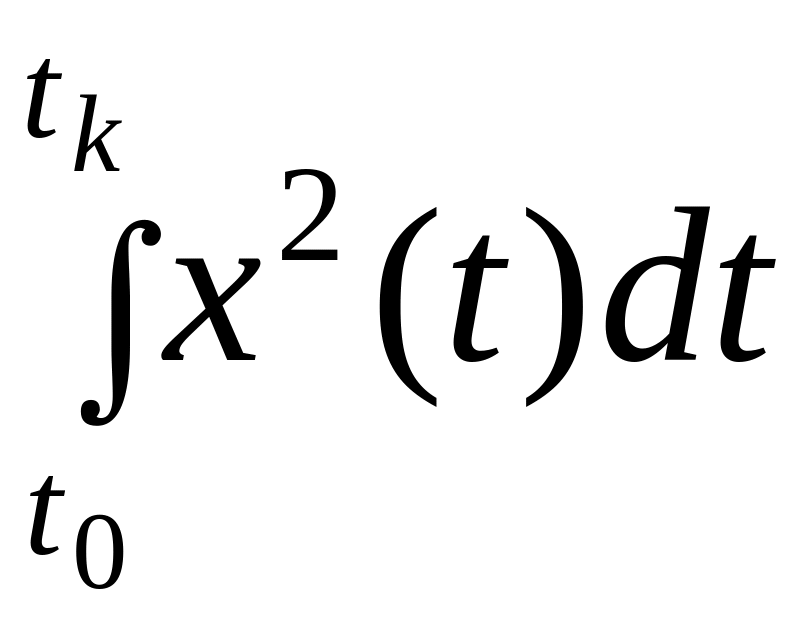запрещает значительные отклонения
от установившегося значения, составляющая
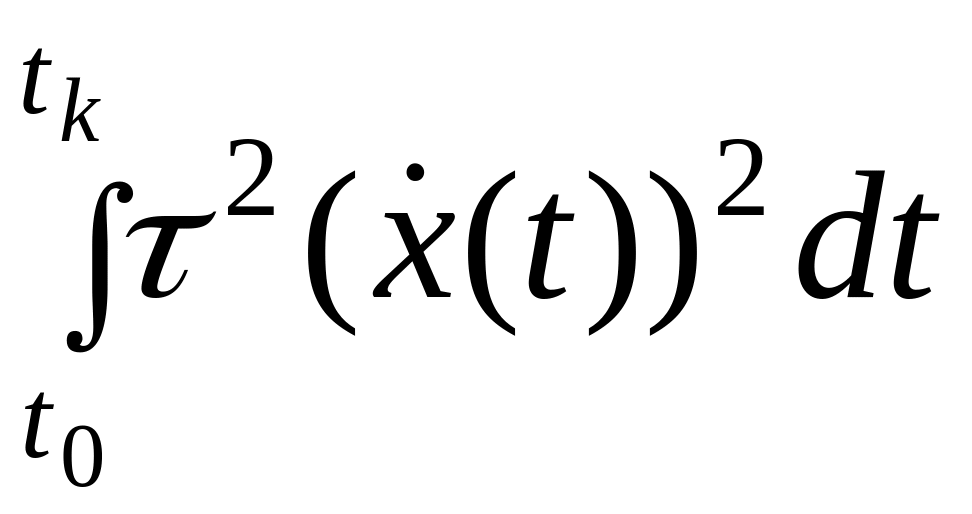запрещает существование больших
производных
.
Таким образом, получается не только
быстрый, но и плавный, без разных колебаний
переходной процесс. Иногда для этих
целей применяется и более сложные оценки
вида:
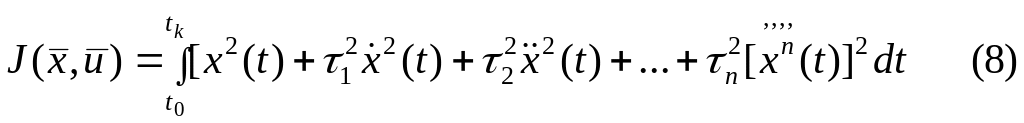
Вообще же квадратичные критерии широко распространенные в теории оптимального управления в самом общем случае содержат и члены зависящие от вектора управления, и слагаемое, учитывающие конечное состояние системы
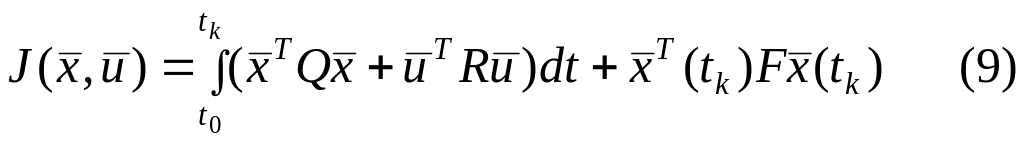
где
-
симметрические матрицы размера,
соответственно
а индекс «Т» означает операцию
транспонирования.
Отметим, что элементов матрица
определяет также технические показатели
качества САУ, как перерегулирования
время
,
точность и т.д. В настоящее время
разработана методика синтеза линейных
САУ по квадратичному критерию (9), которая
дает возможность получить структуру и
параметры оптимального регулятора,
т.е. решить задачу синтеза.
Функция другого вида
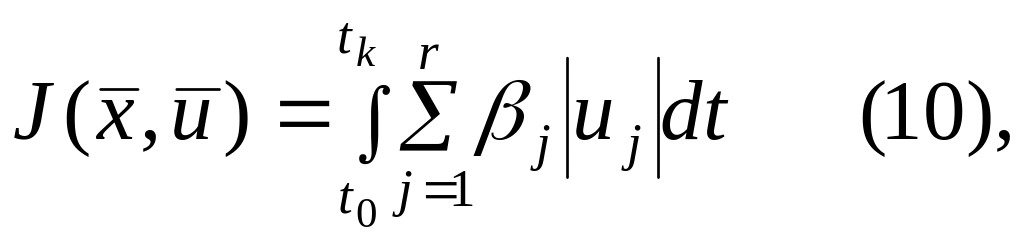где
-
некоторые весовые коэффициенты, позволяют
учесть расход рабочего тела на уравнение.
Задачи, в процессе решения которых
минимизируется функционал (10), называются
задачами оптимизации САУ по расходу
топлива. Такие задачи возникают, например,
при управлении космическими аппаратами,
когда существенным является экономичное
расходование ограниченного количества
горючего, имеющегося на борту.
В некоторых случаях рассматривают задачу минимизации функционала вида
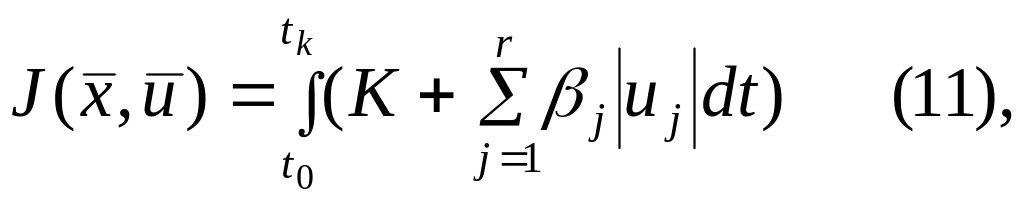где
,
который представляет собой комбинацию
функционалов (4) и (10)- позволяет учесть
как время
,
так и расход топлива.
Выбор того или иного функционала определяется техническими показателями и условиями работы проектируемой САУ и во многом зависит от инструкции и опыта инженера – проектировщика.