Запишем гессиан

Возьмем произвольные направления - не обязательно на градиенту и запишем уравнение параболы, получающейся в сечении поверхности вертикальной плоскостью, проходящей по направлению (как в разобранном примере, только там было направлением градиента).

Раскроем скобки, сделаем приведение подобных и из уравнения , найдем оптимальное значение .

или, с учетом (3) и (4) перепишем это выражение в матричной форме.

Получим выражение для оптимальности по произвольному направлению . Если же за направление взять напрвлеие градиента (антиградиента), то получится:

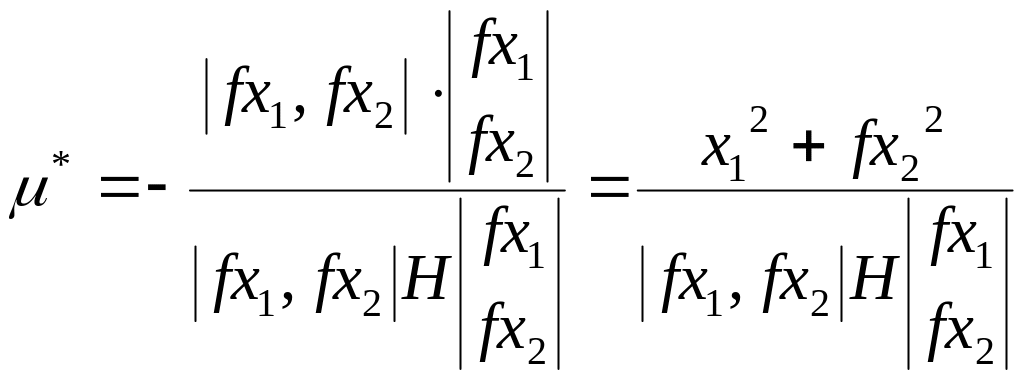
Это для n=2.

Для многомерного случая:

Метод наискорейшего спуска имеет ряд модификаций, например задается в виде некоторого ряда и его не надо.

Для квадратичных функций сепарабельной и несепарабельной можно записать формулу

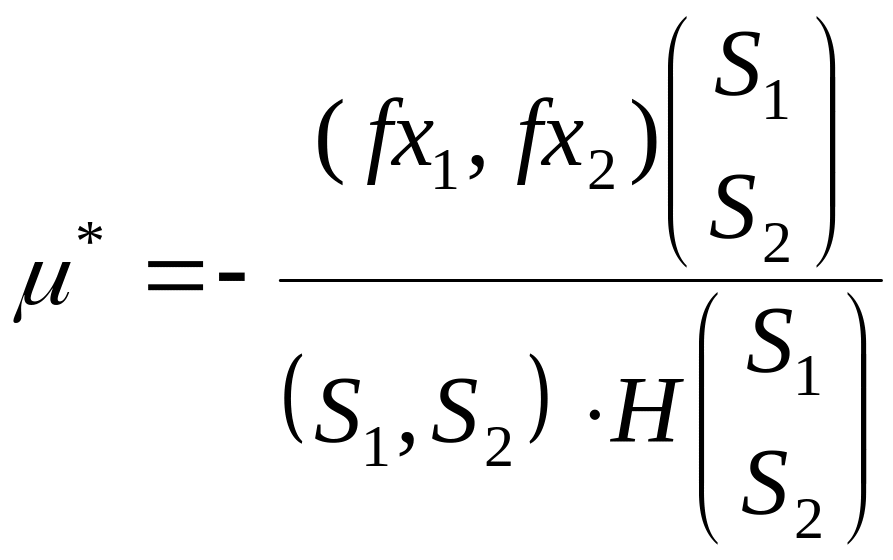
- проекции градиента;

- направления.

Н – матрица Гесса.

Для поиска маке /При поиске min знак –заменяем на +/

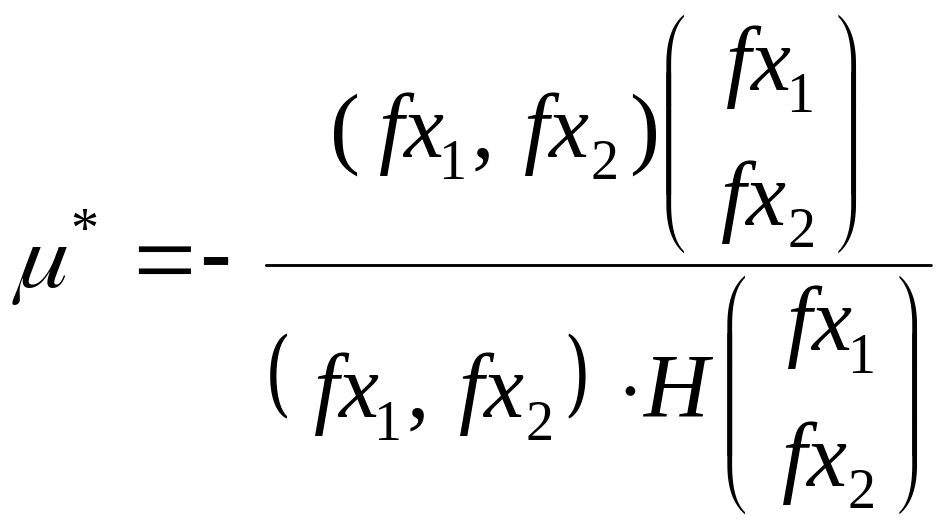для n =2

для любых n

Пример.

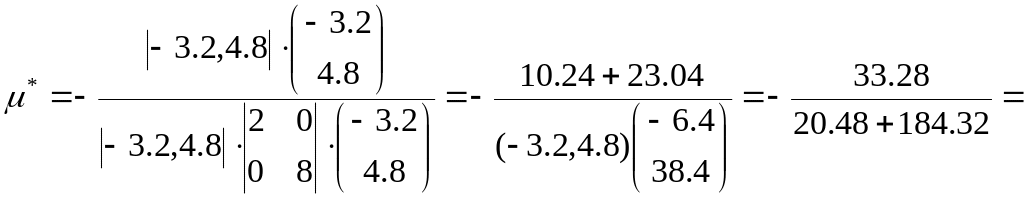
Градиентный метод второго порядка. Метод сопряженных направлений.

Для квадратичных функций можно создать градиентный метод, при котором время сходимости будет конечным и равно числу переменных n.

Назовем некоторое направление и сопряженными по отношению к некоторой положительно определенной матрице Гесса H, если выполняется:

Если ,

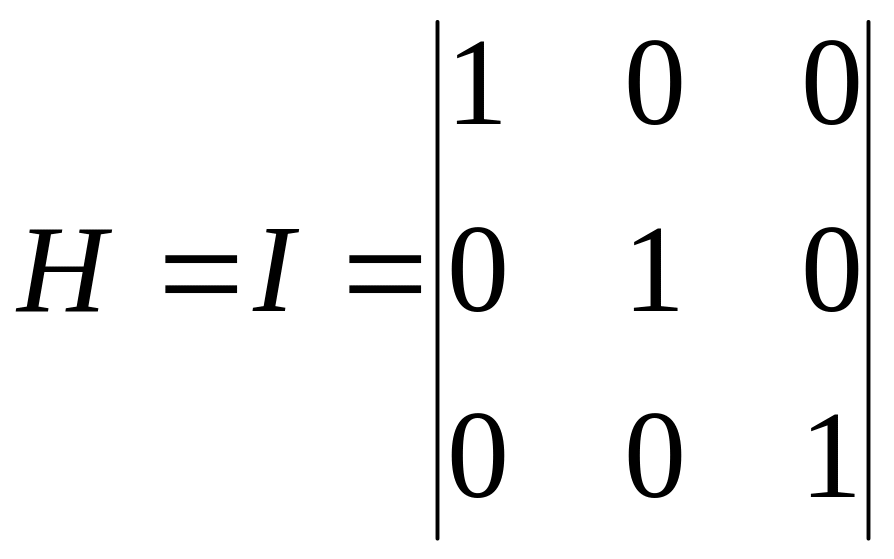Тогда т.е.

Значит при единичной H, сопряженное направление означает их перпендикуляр.

В общем же случае H неединичная. В общем случае сопряженность – это применение матрицы Гесса к вектору - означает поворот этого вектора на некоторый угол и его растяжение или сжатие.

а теперь вектору вектор ортогонален т.е. сопряженность это не ортогональность векторов и , а ортогональность повернутого вектора т.е. и .

Пример.

Зададим из точки любое направление . Пусть

По верхнему extr рассекаем вертик. пл., -её след. Найдем min на направлении . Это нам уже знакомо по методу МНС - метод наискорейшего спуска.

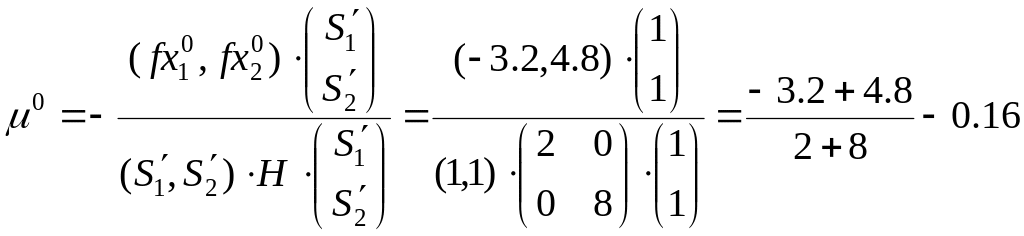
Т.е. шагнули от extr. Это неважно. Определим направление , сопряженное к .

Зададимся

По направлению ищем extr , но так чтобы проходило через точку (пунктир).

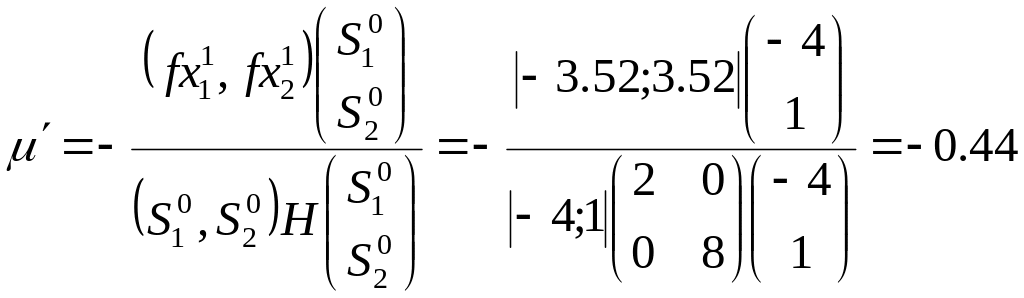
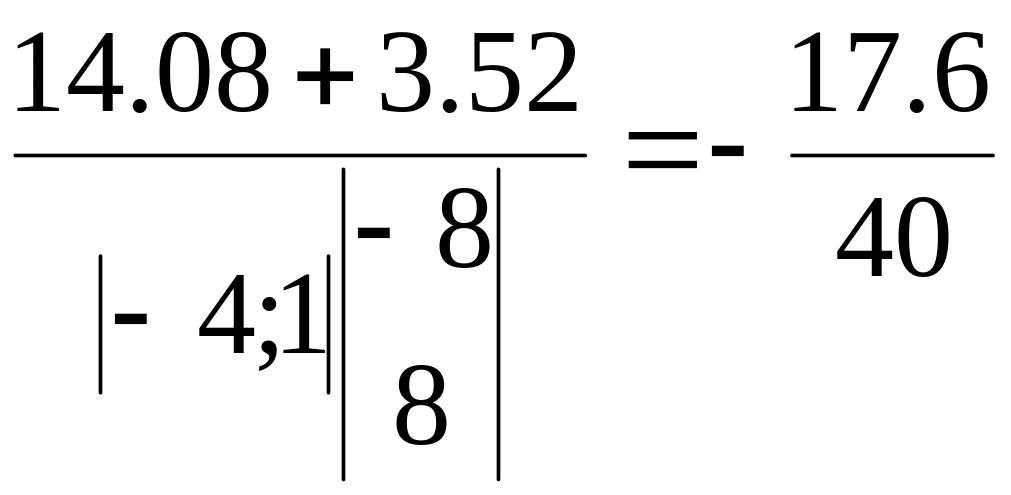, тогда

Т.е .

Таким образом, за 2 итерации для квадратичных функций мы попали в extr.

Геометрический смысл метода сопряженного направления

x₂

Применение H равно сильно повороту осей эллипсов так, чтобы одна из осей проходила через точку А₁(А₂)т.е. за один шаг мы попали на главную ось и следующим шагом попадаем в extr. Вычислять на каждом шаге.

Метод сопряженных градиентов, тоже что и метод сопряженных направлений, только 1-ый шаг делается не в произвольном направлении, а по градиенту.

В технике, как правило, задачи на extr всегда имеют некоторые дополнительные ограничения.

Если задача ставится так:

1. . Найти её extr на ограничениях равенствах . Примечание. Ограничений типа здесь нет, то это классическая задача Лагранжа.

2. Вторая задача (неклассическая). . Найти extr на ограничениях –неравенствах .
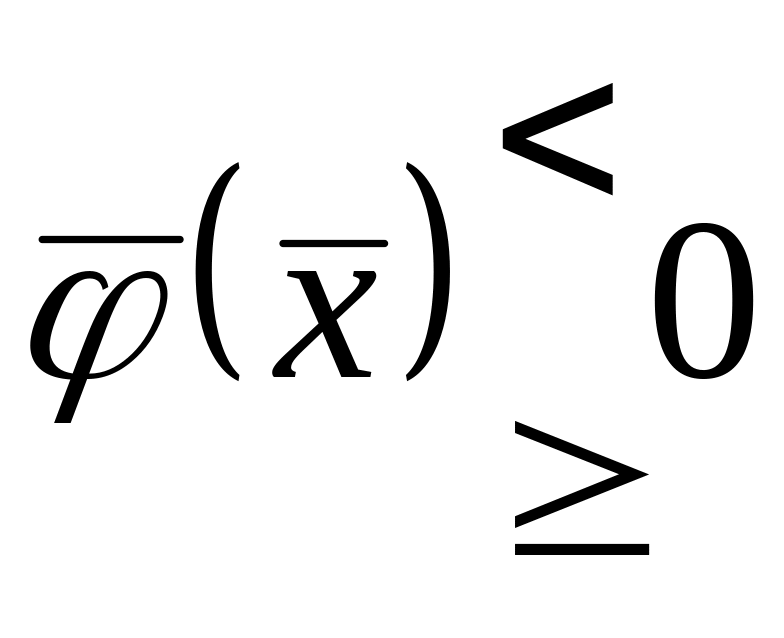