15. Метод Гауса

Метод Гаусса - это метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Решить систему уравнений методом Гаусса:

                                                      x +  y - 3z = 2,

                                                    3x - 2y +  z = - 1,

                                                    2x +  y - 2z = 0.

Решение. Выпишем расширенную матрицу данной системы

и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

 ~ ;

б) третью строку умножим на (-5) и прибавим к ней вторую:

.

В результате всех этих преобразований данная система приводится к треугольному виду:

                                                    x + y - 3z = 2,

                                                    -5y + 10z = -7,

                                                           - 10z = 13.

Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим x = - 0,7.

16. Однородные системы уравнений

Однородной системой линейных уравнений называется система, правая часть которой равна нулю:

Матричный вид однородной системы: Ax=0.

Однородная система всегда совместна, поскольку любая однородная линейная система имеет по крайней мере одно решение:

x₁=0 , x₂=0 , ..., x_n=0.

Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.

Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

17. Фундаментальная система решений

Если однородная система нетривиально совместна, то она имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением. Доказано, что среди бесконечного множества решений однородной системы можно выделить ровно n-r линейно независимых решений. Совокупность n-r линейно независимых решений однородной системы называется фундаментальной системой решений. Любое решение системы линейно выражается через фундаментальную систему. Таким образом, если ранг r матрицы A однородной линейной системы Ax=0  меньше числа неизвестных n и векторы e₁ , e₂ , ..., e_n-r  образуют ее фундаментальную систему решений (Ae_i =0, i=1,2, ..., n-r), то любое решение x системы Ax=0 можно записать в виде

x=c₁ e₁ + c₂ e₂ +  ... + c_n-r e_n-r ,

где c₁ , c₂ , ..., c_n-r — произвольные постоянные. Записанное выражение называется общим решением однородной системы.

Исследовать однородную систему   — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.

Исследуем однородную систему методом Гаусса.

Пусть

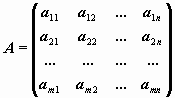
матрица исследуемой однородной системы, ранг которой r< n.

Такая матрица приводится Гауссовым исключением к ступенчатому виду

.

Соответствующая эквивалентная система имеет вид

Отсюда легко получить выражения для переменных x₁ , x₂ , ..., x_r через x_r+1 , x_r+2 , ..., x_n . Переменные x₁ , x₂ , ..., x_r  называют базисными переменными, а переменные x_r+1 , x_r+2 , ..., x_n — свободными переменными.

Перенеся свободные переменные в правую часть, получим формулы

которые определяют общее решение системы.

Положим последовательно значения свободных переменных равными

и вычислим соответствующие значения базисных переменных. Полученные n-r решений линейно независимы и, следовательно, образуют фундаментальную систему решений исследуемой однородной системы: