12. Системы линейных уравнений, основные понятия, матричная запись

Совокупность уравнений

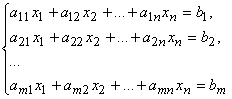
относительна неизвестных x₁, x₂, ..., x_n-1, x_n называется системой линейных алгебраических уравнений.

Числа a_ij — коэффициенты системы, b_i— правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.

Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется решением системы.

Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.

Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.

Если среди правых частей b_i системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.

Если все правые части системы равны нулю, то система называется однородной.

Система линейных уравнений может быть записана в матричной форме A·x = b:

Здесь A — матрица системы, b — правая часть системы , x— искомое решение системы.

Иногда удобно записывать систему линейных уравнений в другой матричной форме:

A⁽¹⁾x₁ + A⁽²⁾x₂ + ... + A⁽ⁿ⁾x_n = b. Здесь  A⁽¹⁾, A⁽²⁾, ... , A⁽ⁿ⁾ — столбцы матрицы системы.

Матрица Ap называется расширенной матрицей системы.

Если исследуется неоднородная система A·x = b, b ≠ 0, то система A·x =0 называется приведенной однородной системой для системы A·x = b.

13. Правило Крамера

Если в системе линейных уравнений с неизвестными , то система имеет решение и притом единственное. Это решение задается формулами

Решите систему уравнений

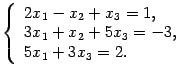
Решение. Выписываем матрицу системы 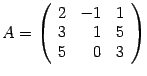и столбец свободных членов .

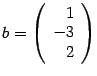Находим определитель системы: 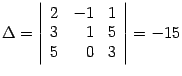. Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:

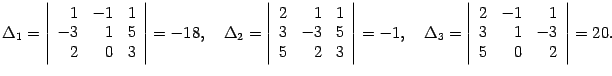
Итак,

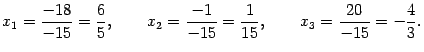
Ответ: .         

        Замечание 15.1   При кажущейся простоте правила Крамера применяется оно для систем более, чем из трех уравнений, только в каких-то исключительных случаях. Дело в том, что вычисление определителей требует выполнения большого числа арифметических операций и существует способ, требующий меньшей вычислительной работы. Этот способ будет описан позже.         

        Замечание 15.2   При решении системы уравнений приходится выполнять довольно большой объем вычислений. Поэтому велика вероятность ошибки. Чтобы обнаружить эту ошибку, рекомендуется выполнить проверку ответа, то есть подставить полученные значения неизвестных в уравнения системы. Если все уравнения превратятся в верные равенства, то решение найдено верно. В противном случае при вычислениях где-то допущена ошибка.         

14. Теорема Кронекера-Капелли

Система совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.

Доказательство.

1. Необходимость: пусть система совместна и 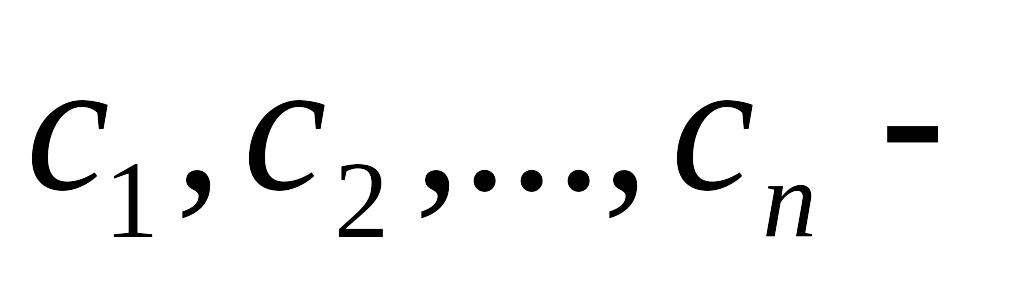ее решение. Тогда

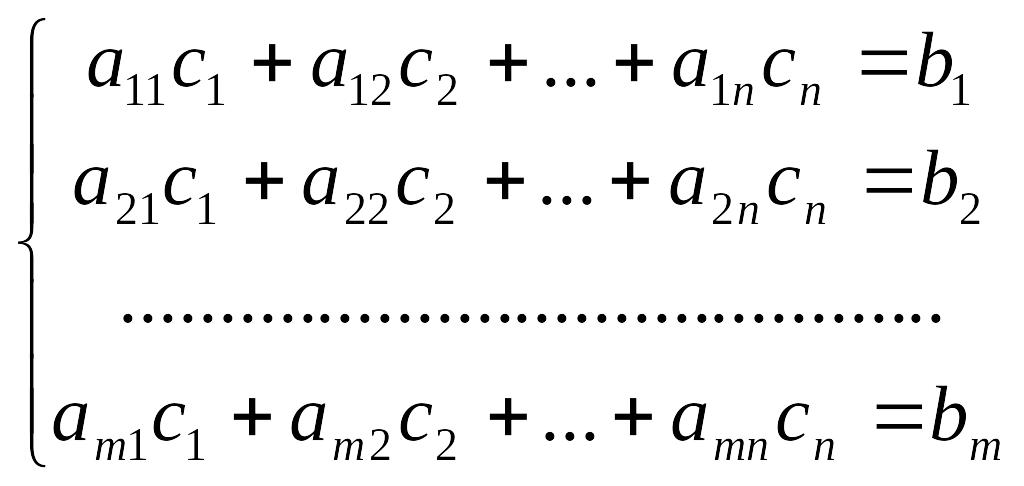, то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть

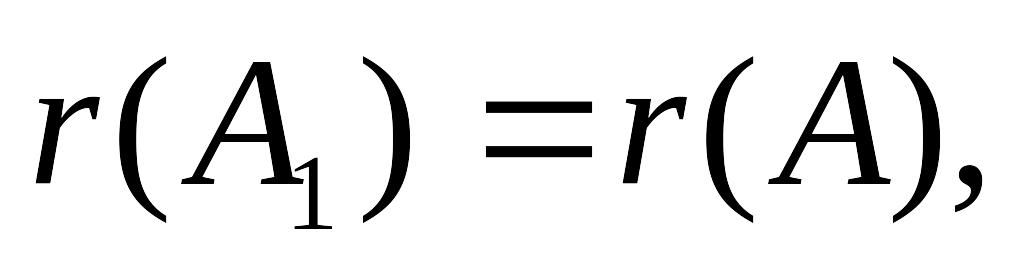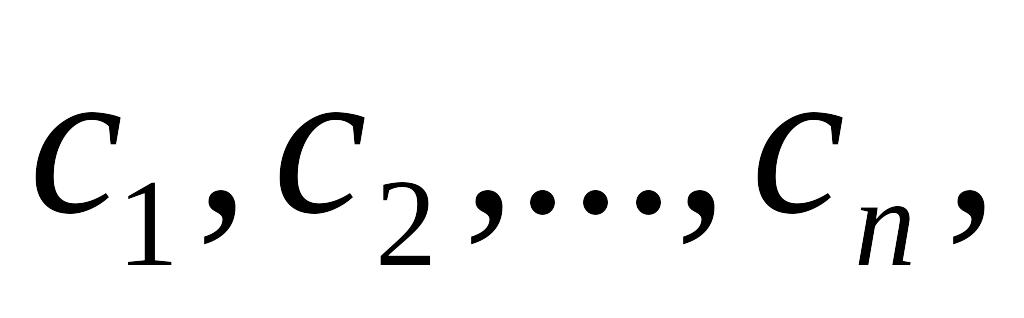2. Достаточность: если то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации то эти числа будут решением системы, т.е. эта система совместна. Теорема доказана.