8. Решение простейших матричных уравнений.

 Уравнение, называется матричным, если в качестве неизвестного оно содержит матрицу. Простейшие матричные уравнения имеют вид

, (1.24)

,  (1.25)

, (1.26)

где  – известные матрицы, а  – неизвестные матрицы соответствующих размеров. В общем случае уравнения (1.24)-(1.26) эквивалентны некоторым системам линейных алгебраических уравнений (СЛАУ), но в том частном случае, когда матрицы   и  обратимы, теория этих уравнений проста. Прежде чем изложить её отметим, что числовая матрица  является решением уравнения (1.24), если при подстановке её в это уравнение вместо матрицы  мы получаем верное матричное равенство (и аналогично для уравнений (1.25) и (1.26)).

9. Линейная зависимость и независимость столбцов и строк

Столбец называется линейной комбинацией столбцов одинаковых размеров, если

(3.1)

где — некоторые числа. В этом случае говорят, что столбец разложен по столбцам , а числа называют коэффициентами разложения. Линейная комбинация с нулевыми коэффициентами называется тривиальной.

Система из столбцов называется линейно независимой, если равенство (3.2) возможно только при , т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).

Замечания 3.1

1. Один столбец тоже образует систему: при — линейно зависимую, а при линейно независимую.

2. Любая часть системы столбцов называется подсистемой.

10. Ранг матрицы.(дать два определения)

Рангом матрицы называется ранг любого оператора, представляемого этой матрицей, т.е. размерность образа этого оператора.

Таким образом, если удастся найти какой–нибудь способ вычисления ранга матрицы, то ранг оператора можно будет определить по рангу его матрицы. Такой способ предлагается в следующем утверждении.

Теорема. Ранг матрицы равен максимальному числу ее линейно независимых столбцов.

Наибольший из порядков миноров матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A).

11. Методы нахождения ранга матрицы

Одним из способов вычисления ранга матрицы является метод окаймления миноров. Рассмотрим применение этого способа на следующем примере.

Пример. Определить ранг матрицы

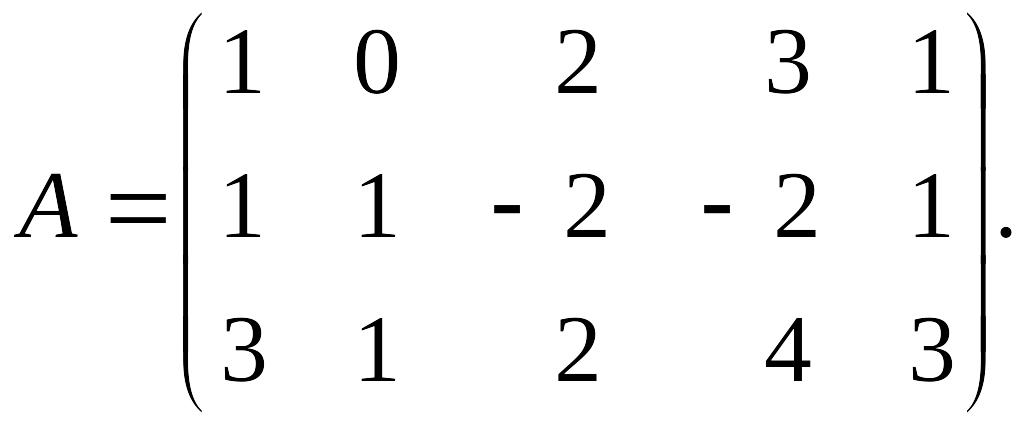
Среди миноров второго порядка матрицы  существует, по крайней мере, один, отличный от нуля. Например, минор матрицы  полученный вычёркиванием из этой матрицы третьей строки, третьего, четвёртого и пятого столбцов, отличен от нуля:

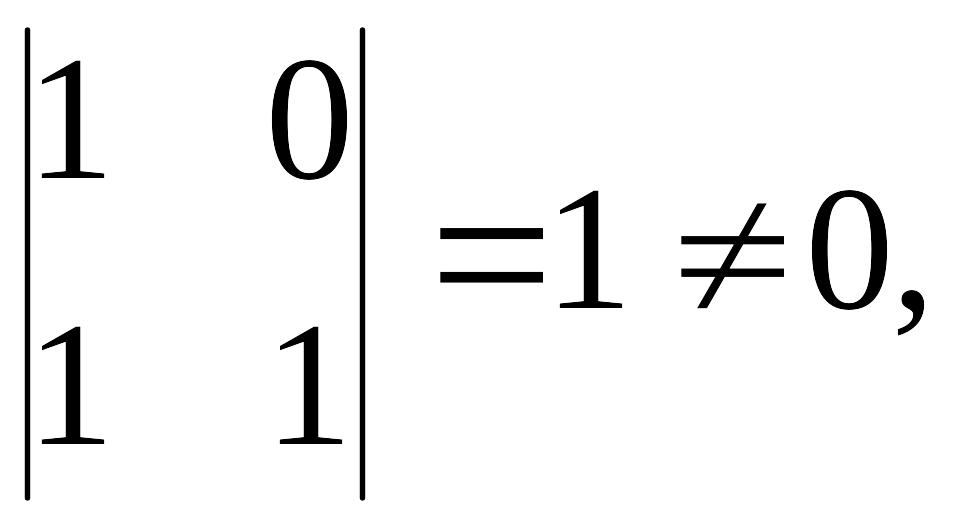
следовательно, ранг данной матрицы не меньше двух.

Найдём миноры третьего порядка матрицы Все десять миноров третьего порядка равны нулю, поэтому ранг данной матрицы не может быть равен трём. Таким образом,

Другой способ вычисления ранга матрицы основан на применении элементарных преобразований матрицы и использовании следующих утверждений.

Теорема 4.1. Ранг ступенчатой матрицы равен количеству её ненулевых строк.

Теорема 4.2. Элементарные преобразования матрицы не изменяют её ранг.

Пример. Вычислим ранг матрицы из предыдущего примера. Для этого матрицу  с помощью элементарных преобразований приведём к ступенчатому виду. Найдём сумму второй строки матрицы  с первой строкой, умноженной на  а также сумму третьей строки матрицы  с первой строкой, умноженной на  В результате указанных элементарных преобразований получим эквивалентную матрицу

Третью строку полученной матрицы сложим с её первой строкой, умноженной на  и получим эквивалентную матрицу

Удалим из этой матрицы третью строку и получим ступенчатую эквивалентную матрицу, количество ненулевых строк которой равно двум:

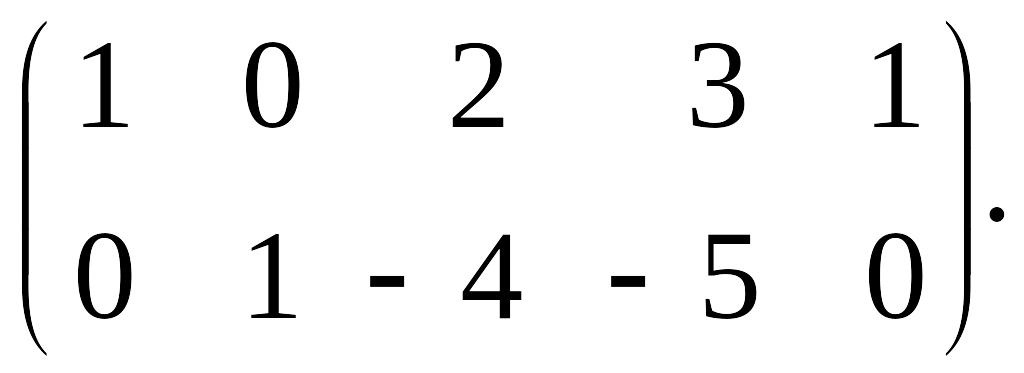
В соответствии с теоремой 4.1, ранг полученной матрицы равен двум, а значит (теорема 4.2),