6. Определитель произведения матриц

Пусть и - квадратные матрицы одного и того же порядка. Тогда

т.е. определитель произведения матриц равен произведению их определителей.

Доказательство теоремы проводится в три этапа. Во-первых, теорема справедлива, если один из сомножителей имеет простейший вид (см. рис. 1.6). Пусть, например, матрица квадратная л-го порядка имеет простейший вид: . Если , то в произведении последние строк будут нулевыми. Тогда по свойствам 1,2 определителей: и , т.е. равенство верно. Если же , то А = - единичная матрица. Тогда

т.е. равенство справедливо. Аналогично рассматривается случай, когда матрица имеет простейший вид.

Второй этап - доказательство формулы для элементарных матриц. Если матрица элементарная вида (1.1), (1.3) или (1.5), то ее определитель равен или 1 соответственно, а произведение есть элементарное преобразование столбцов матрицы . По свойствам 1, 3, 6 или 9 определителей убеждаемся в справедливости.

Третий этап - доказательство формулы для произвольных квадратных матриц n-го порядка. По теореме любую квадратную матрицу можно представить в виде произведения простейшей (она является элементарной) и элементарных преобразующих матриц:

и .

Тогда, используя результат первых двух этапов, можно записать,что и требовалось доказать.

7. Обратная матрица. Алгоритм нахождения обратной матрицы.

Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Матрица, обратная матрице А, обозначается через А^-1, так что В = А^-1. Обратная матрица вычисляется по формуле

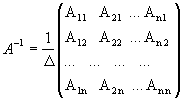,                                               (4.5)

где А _{i j} - алгебраические дополнения элементов a _{i j}.

Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований . Любую неособенную матрицу А путем элементарных преобразований только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А элементарные преобразования в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать элементарные преобразования над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

Для матрицы  найти обратную.

Решение. Находим сначала детерминант матрицы А 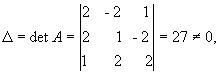    значит, обратная матрица существует и мы ее можем найти по формуле:   , где А_{i j} (i,j=1,2,3) - алгебраические дополнения элементов а_{i j} исходной матрицы.                  

                   

                  

                 

 откуда   .
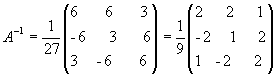