3.2.1 Режими роботи трифазної системи при з'єднанні споживачів зіркою

Режими роботи трифазної мережі, споживачів з'єднаних зіркою, можуть виникати різного типу та характеру. Розглянемо деякі з них:

• симетричний Z_аb = Z_bс = Z_са;

• несиметричний Z_аb ≠ Z_bс ≠ Z_са:

а) обрив фазного проводу;

б) обрив лінійного проводу;

с) ввімкнення в одну із фаз споживачів з активним та активно-індуктивним навантаженням.

Застосовують трипровідну та чотирипровідну схеми з'єднання приймачів зіркою. Трифазні симетричні споживачі електричної енергії вмикають згідно трипровідної схе­ми (без нульового проводу). Типовим навантаженням такого типу є трифазні асинхронні двигуни. Несиметричні приймачі електричної енергії вмикаються згідно чотирипровідної схеми (з нульовим проводом).

3.2.1.1 Симетричне навантаження фаз споживачів

При симетричному навантаженні (Z_а = Z_b = Z_с, φ_а = φ_b = φ_с= arctq (Х_Ф/R_Ф), або Z_а = Z_b = Z_с) діючі значення стру­мів у фазах однакові (I_а= I_b= I_с = I_Ф, або İ_а= İ_b= İ_с = İ_Ф). Вектор струму в нейтральному проводі Ī_n (İ_n) дорівнює геометричній сумі векторів фазних стру­мів Ī_а + Ī_b + Ī_с = 0, або İ_а + İ_b + İ_с = 0 (рисунок 3.4 і 3.5,а).

При симетричному навантаженні і з’єднанні споживачів зіркою справедливе співвідношення між лінійними та фазними напругами і струмами:

UЛ = UФ; ІЛ = ІФ.

Рисунок 3.4 – Електрична схема з’єднання фаз споживача зіркою

Значення діючих лінійних та фазних струмів визначаються за формулами:

Комплексні значення фазних напруг:

_а = U_а e ^{j0 º};

_b = U_b e ^{– j 120 º};

_с = U_с e ^{– j 240 º}.

Тоді, комплексні значення лінійних напруг:

_аb = _a – _b = U_а e ^{j 30 º};

_bс = _b – _с = U_b e ^{– j 90 º};

_са = _с – _а = U_с e ^{– j 210 º}.

Комплексні значення фазних струмів (І_Л = І_Ф):

İ_а = _а / Z _а;

İ_b = _b / Z _b;

İ_с = _с / Z _с.

Струм у нульовому проводі:

İ_n = İ_а + İ_b + İ_с = 0

На рисунку 3.5,а показана векторна діаграма напруг і струмів при симетричному активному навантаженні (R_А =R_В = R_С), на рисунку 3.5,б – при симетричному активно-індуктивному навантаженні,

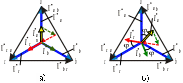
Рисунок 3.5 – Векторні діаграми напруг та струмів при з’єднанні фаз споживачів зіркою:

а) При симетричному активному навантаженні;

б) При симетричному активно-індуктивному навантаженні

3.2.1.2 Несиметричне навантаження фаз споживачів

При несиметричному навантаженні (Z_а ≠ Z_b ≠ Z_с, φ_а ≠ φ_b ≠ φ_с= arctq (Х_Ф/R_Ф), або Z_а ≠ Z_b ≠ Z_с) діючі значення стру­мів у фазах неоднакові (I_а ≠ I_b ≠ I_с, або İ_а ≠ İ_b ≠ İ_с). Вектор струму в нейтральному проводі Ī_n (İ_n) дорівнює геометричній сумі векторів фазних стру­мів Ī_а + Ī_b + Ī_с ≠ 0, або İ_а + İ_b + İ_с ≠ 0 (рисунок 3.4 і 3.5,а).

На рисунку 3.6 показана векторна діаграма напруг і струмів при несиметричному активному навантаженні (R_а = R_с ≠ R_b). Струм в нейтральному проводі не дорівнює нулеві İ_n ≠ 0.

Рисунок 3.6 – Векторні діаграми напруг і струмів при з’єднанні фаз споживачів зіркою та

несиметричному активному навантаженні

В чотирипровідній системі при обриві фазного проводу, наприклад фазного проводу а – n (рисунок 3.7.а) фазний струм І_Ф = 0 (І_а = 0). Лінійні та фазні напруги залишаються без змін (рисунок 3.7.б):

U_аb = U_bс = U_са = U_Л, U_а = U_b = U_с = U_Ф.

Електрична схема та векторна діаграма для цього режиму приведені на рисунку 3.7.

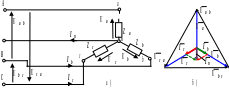
Рисунок 3.7 – Електрична схема з’єднання фаз споживачів зіркою а)

та векторна діаграма б) при обриві фазного проводу

При обриві лінійного проводу в чотирипровідній системі (рисунок 3.8.а), наприклад обрив лінійного проводу А-а, струм І_Ф = І_Л = 0 (І_а = 0, І_b = І_с), а напруги (рисунок 3.8.б):

U_а = 0, U_bс = U_Л, U_аb = U_са = U_b = U_с = U_Ф.

Електрична схема та векторна діаграма для цього режиму приведені на рисунку 3.8.

Рисунок 3.8 – Електрична схема з’єднання фаз споживачів зіркою а)

та векторна діаграма б) при обриві лінійного проводу

При відсутності нейтрального проводу і несиметричному навантаженні (рисунок 3.2 і 3.9), між нейтральними точками генератора і навантаження (Nn) виникає напруга зміщення нейтралі:

,

де Y _а, Y _b, Y _с – комплексні провідності фаз споживачів (Y = 1/ Z).

У цьому випадку фазні напруги споживачів не утворюють симетричну трифазну систему і визначаються за формулами:

_a = _А – _{N n} , Ū_a = Ū_А – Ū _{N n} ,

_b = _В – _{N n} , Ū_b = Ū_В – Ū _{N n} ,

_с = _С – _{N n} , Ū_с = Ū_С – Ū _{N n} .

А векторна сума струмів:

Ī_а + Ī_b +Ī_с = 0.

Рисунок 3.9 – Електрична схема з’єднання фаз споживачів зіркою

при відсутності нейтрального проводу

Векторна діаграма напруг і струмів трифазної трипровідної мережі при несиметричному активному навантаженні наведена на рисунку 3.10.

Рисунок 3.10 – Векторна діаграми напруг і струмів трифазної трипровідної мережі

при несиметричному активному навантаженні

На рисунку 3.11,а наведена векторна діаграма напруг і струмів для трипровідної мережі при обриві фазного проводу (наприклад, фазного проводу а – n). На рисунку 3.11,б наведена векторна діаграма напруг і струмів при несиметричному активному навантаженні і відсутності нейтрального проводу (навантаження фази А зменшене (R_А > R_В = R_С).

Рисунок 3.11 – Векторна діаграми напруг і струмів трифазної

трипровідної мережі:

а) При обриві фазного проводу а – n;

б) При несиметричному навантаженні без нейтрального проводу