
- •I. Элементы теории вероятности
- •1. Вероятность по лапласу (Классическая вероятность)
- •2. Элементы комбинаторики
- •2. Основные теоремы комбинаторики.
- •2.2.Перестановки с повторениями.
- •2.3. Упорядоченные множества. Размещения без повторений.
- •2.4. Размещения с повторениями.
- •2.5. Сочетания.
- •2.6. Свойства сочетаний. Формула бинома Ньютона.
- •3. Методы решения комбинаторных задач.
- •1.2 Действия над событиями
- •1.3 Свойства операций над событиями
- •1.4. Геометрическая вероятность
- •2. Вероятность по мизесу (Статистическая вероятность)
- •3. Вероятность по колмогорову (Аксиоматическая вероятность)
- •2. Принципы теории вероятностей.
- •2.1. Принцип сложения.
- •2.2. Принцип умножения.
- •2.3. Полная вероятность и формула Байеса
- •3. Схемы испытаний
- •Случайные величины
- •Повторные испытания.
- •Распределения, связанные с повторными испытаниями.
- •Двумерные случайные величины
- •Свойства функции распределения.
- •Элементы математической статистики
- •1. Что такое математическая статистика?
- •2. Понятие выборки.
- •3. Построение вариационных рядов
- •Точечные оценки параметров генеральной совокупности по выборочным совокупностям, их свойства. Точечные оценки для математического ожидания и дисперсии случайной величины
- •Оценка для математического ожидания случайной величины
- •Оценка для дисперсии случайной величины
- •Интервальные оценки. Доверительный интервал. Нахождение доверительных интервалов для математического ожидания и дисперсии нормального распределения случайной величины
- •1. Доверительный интервал для оценки математического ожидания нормального распределения случайной величины с известным
- •2. Доверительный интервал для оценки математического ожидания нормального распределения с неизвестным
- •3. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения
- •Статистическая проверка гипотез. Статистическая гипотеза. Нулевая и конкурирующая гипотеза. Статистический критерий. Критическая область
3. Построение вариационных рядов
Пусть
из генеральной совокупности извлечена
выборка, причем
![]() наблюдалось
наблюдалось
![]() раз,
раз,
![]() раз и т.д.,
раз и т.д.,
![]() раз и
раз и
![]() –
объем выборки.
–
объем выборки.
Наблюдаемые
значения
![]() называются вариантами; последовательность
вариант, записанных в порядке возрастания,
называют вариационным
рядом.
называются вариантами; последовательность
вариант, записанных в порядке возрастания,
называют вариационным
рядом.
Числа
наблюдений
![]() обозначены
обозначены
![]() и называются частотами,
а величины
и называются частотами,
а величины
![]() –
относительными
частотами. Статистическим распределением
выборки называется
перечень вариант
–
относительными
частотами. Статистическим распределением
выборки называется
перечень вариант
![]() и соответствующих частот
и соответствующих частот
![]() (или
относительных частот
(или
относительных частот
![]() ):
):
Х |
|
|
... |
|
nx |
|
|
... |
|
Wx |
|
|
... |
|
В случае большого количества вариантов и непрерывного распределения признака статистическое распределение выборки задают в виде последовательности интервалов и соответствующих им частот. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на определенное число частичных интервалов (x0, x1), (x1, x2),...,(xk-1, xk) длиной хi и находят для каждого интервала ni сумму частот вариантов, попавших в i-й интервал. Таким образом получают интервальное статистическое распределение выборки:
Интервалы |
(x0, x1) |
(x1, x2) |
... |
(xk-1, xk) |
nx |
|
|
... |
|
Wx |
|
|
... |
|
Статистическое распределение выборки называют также статистическим рядом.
Для графического изображения статистического ряда используют полигоны и гистограммы.
Для
построения полигона
на оси Ох откладывают значения вариант,
на оси ординат –
значения частот
![]() (или относительных частот
(или относительных частот
![]() ).
Построенную таким образом ломаную,
отрезки которой соединяют точки (
).
Построенную таким образом ломаную,
отрезки которой соединяют точки (![]() или
или
![]() ,
называют полигоном
частот или
полигоном
относительных частот соответственно.
,
называют полигоном
частот или
полигоном
относительных частот соответственно.
В
случае непрерывного распределения
признака на основании интервального
статистического распределения используют
гистограмму,
устанавливающую зависимость частот от
разрядов интервалов, в которые попадают
значения случайной величины. Предполагаем,
что длины интервалов равны
![]() (h –
шаг распределения). На оси Ox отметим
точки
(h –
шаг распределения). На оси Ox отметим
точки
![]() с шагом
с шагом
![]() друг от друга. На каждом частичном
интервале строим прямоугольник высотой
друг от друга. На каждом частичном
интервале строим прямоугольник высотой
![]() (плотность частоты). Гистограммой
частот
называют ступенчатую фигуру, состоящую
из вышеупомянутых прямоугольников.
Поскольку площадь i-го частичного
прямоугольника равна
(плотность частоты). Гистограммой
частот
называют ступенчатую фигуру, состоящую
из вышеупомянутых прямоугольников.
Поскольку площадь i-го частичного
прямоугольника равна
![]() ,
то площадь
гистограммы частот равна
сумме всех частот, т.е. объему выборки
n.
,
то площадь
гистограммы частот равна
сумме всех частот, т.е. объему выборки
n.
Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h, а
высоты равны отношению
![]() (плотность относительной частоты). Для
построения гистограммы относительных
частот на оси абсцисс откладывают
частичные интервалы, а над ними проводят
прямоугольники высотой
.
Площадь i-го прямоугольника равна
(плотность относительной частоты). Для
построения гистограммы относительных
частот на оси абсцисс откладывают
частичные интервалы, а над ними проводят
прямоугольники высотой
.
Площадь i-го прямоугольника равна
![]() –
относительной частоте вариант, попавших
в i-й интервал. Следовательно, площадь
гистограммы относительных частот равна
сумме всех относительных частот, т.е.
единице. Поэтому гистограмма относительных
частот является статистическим аналогом
плотности распределения случайной
величины X.
–
относительной частоте вариант, попавших
в i-й интервал. Следовательно, площадь
гистограммы относительных частот равна
сумме всех относительных частот, т.е.
единице. Поэтому гистограмма относительных
частот является статистическим аналогом
плотности распределения случайной
величины X.
Задача В результате испытаний случайной величины X получен статистический ряд:
I |
0-5 |
5-10 |
10-15 |
15-20 |
20-25 |
nx |
3 |
5 |
4 |
8 |
5 |
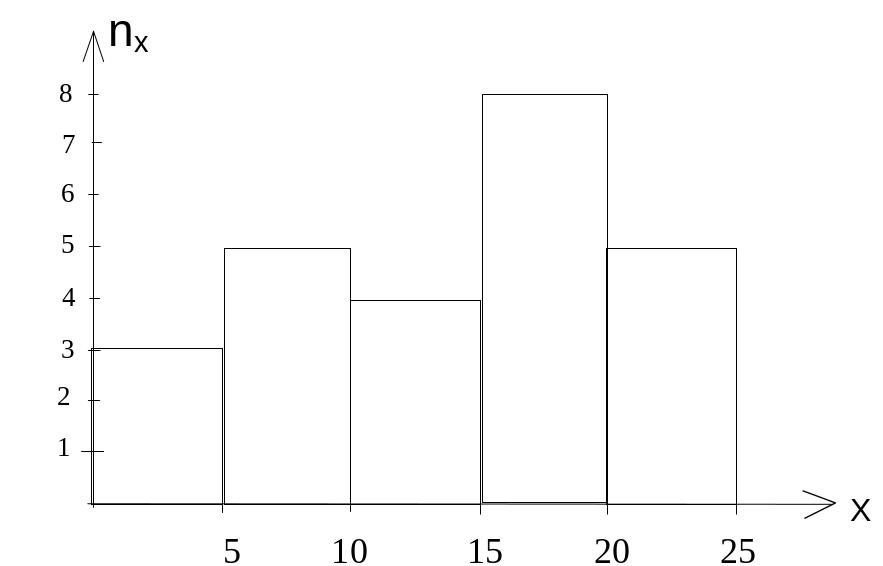
Построить гистограмму частот и гистограмму относительных частот статистического ряда.
Решение. На рис. показана гистограмма частот
Построим статистический ряд относительных частот
I |
0-5 |
5-10 |
10-15 |
15-20 |
20-25 |
|
0,12 |
0,2 |
0,16 |
0,32 |
0,2 |
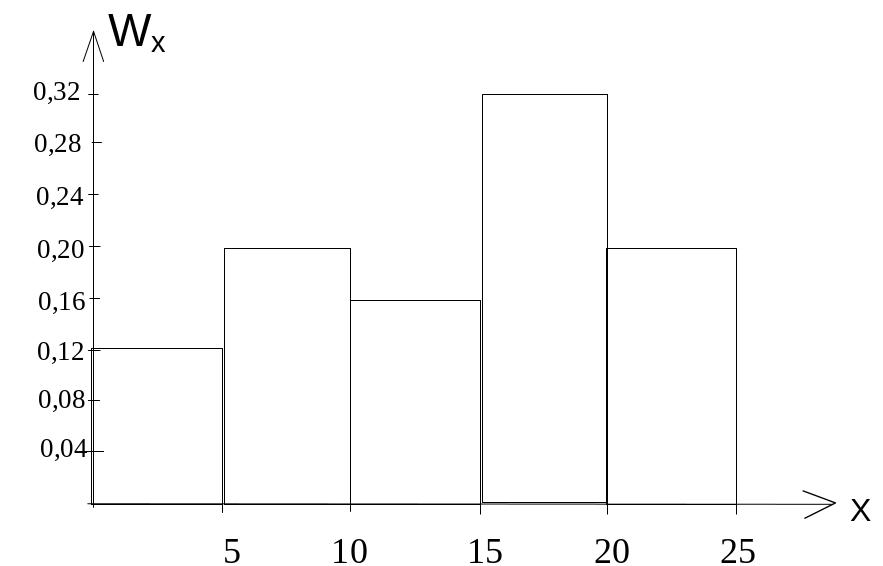
Пусть теперь изучается случайная величина X, закон распределения которой неизвестен. Требуется определить закон распределения на основании статистических данных.
Определение
Статистической
(эмпирической) функцией распределения
(иначе функцией распределения выборки)
называют
функцию
![]() ,
определяющую для каждого значения х
относительную
частоту события
,
определяющую для каждого значения х
относительную
частоту события
![]() :
:
![]() ,
,
где
![]() –
число наблюдений, при которых значение
признака X меньше x; n –
объем выборки.
–
число наблюдений, при которых значение
признака X меньше x; n –
объем выборки.
В
отличие от эмпирической функции
распределения
выборки функция распределения
![]() генеральной совокупности называется
теоретической
функцией распределения.
Различие между эмпирической
и теоретической
функциями распределения состоит в том,
что
определяет вероятность события
,
а
относительную частоту этого же события.
Поэтому
можно использовать для приближенного
представления теоретической функции
распределения генеральной совокупности.
генеральной совокупности называется
теоретической
функцией распределения.
Различие между эмпирической
и теоретической
функциями распределения состоит в том,
что
определяет вероятность события
,
а
относительную частоту этого же события.
Поэтому
можно использовать для приближенного
представления теоретической функции
распределения генеральной совокупности.
Функция обладает свойствами :
1) значения эмпирической функции распределения принадлежат отрезку [0,1];
2)
является неубывающей функцией на
промежутке
![]() ;
;
3)
если
–
наименьшая варианта, то
=
0 при
![]() ;
;
если
–
наибольшая варианта, то
= 1 при
![]() .
.
Задача 2. Построить эмпирическую функцию распределения по статистическому распределению
X |
11 |
12 |
13 |
14 |
Wx |
0,4 |
0,1 |
0,3 |
0,2 |
Решение. Имеем
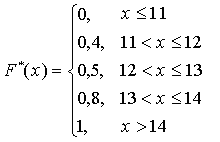 .
.
