13.12. Рівняння пуассона і лапласа

Розглянуті вище вирази для визначення скалярного потенціалу і век­тора напруженості електричного поля (метод суперпозиції та інтегральна форма теореми Ґаусса) застосовують при розрахунку полів простої конфі­гурації. Загалом розрахунок полів зводиться до розв'язання рівнянь Пуас­сона або Лапласа. Відомо, що відношення повного потоку вектора напру­женості через замкнену поверхню до об'єму, що його обмежує, або дивер­генція напруженості, становить

й\уЕ = р/є_а,

де напруженість електричного поля пов'язана з його градієнтом відношен­ням

Е = -Уф = -нгас1ф.

Підставивши його у рівняння дивергенції, отримаємо вираз

аг^гааф = -р/є_а,

вякому отл^гаа¹ називаютьлапсасіаном і позначають символом V .

Отже, дивергенція напруженості електричного поля, записана віднос­но скалярного потенціалу електричного поля складної конфігурації, на­бере вигляду ₉

У> = -р/є_а.

Це рівняння називають рівнянням Пуассона.

Якщо в об'ємі, параметри електричного поля якого розраховують, не­має заряджених частинок (0 = 0) і їхня об'ємна густина відповідно дорів^ нює нулю (р = 0), то рівняння Пуассона набере вигляду

У²ср = 0.

Це рівняння називають рівнянням Лапласа.

Після інтегрування розв'язок рівняння Пуассона має вигляд

V

рсіУ

<)4тіс_;/-

Скалярний потенціал полегшує розрахунок електростатичного поля, оскільки відшукують лише одну скалярну величину ф, знаючи яку, мож­на визначити іншу векторну величину -напруженість поля

£---^гас1ф.

Безпосереднє ж визначення напруженості електричного поля зарівнян-

ням

сігу/і -р/є_а

потребує одночасного визначення трьох скалярних функцій, які підпо­рядковані виразу

а¹? (ІЕ сіЕ _р

(ііу/.-; ,⁴ + --/ + , • *

сіх сіу сії е_а

що значно складніше.

13.13. ПРОВІДНИКИ В ЕЛЕКТРИЧНОМУ полі

Якщо провіднику падати деяку кількість однакового заряду, то під дією сил відштовхування частинки цього заряду пересуватимуться по провідни­ку і зосередяться у поверхневому його шарі. Всередині провідника не буде електростатичного поля і вектора напруженості відповідного значення, тобто Е = 0. Тому поверхню провідника, яка матиме однаковий потенціал,

можна розглядати як першу еквіпотен­ціальну поверхню.

Уразі внесення металевого провід­ника у зовнішнє електричне поле його вільні електрони почнуть зміщатися по перерізу провідника на його поверх­ню, як показано на рис. 13.12. Напру­женість електричного поля по перері­зу провідника дорівнюватиме нулю. Отже, поверхню провідника можна розглядати як межу для зовнішнього

електростатичного поля, локалізованого у діелектрику середовища (отвір у зовнішньому полі). Цей фізичний ефект застосовують при екрануванні об'єктів від зовнішнього електростатичного поля.

13.14. ЕНЕРГІЯ ВЗАЄМОДІЇ ТОЧКОВИХ ЗАРЯДЖЕНИХ ТІЛ

Енергія взаємодії двох зарядів 0_{ та 0₂ дорівнює роботі, яку треба здійснити проти сил їх відштовхування.

Якщо один із зарядів нерухомий, а другий здатний пересуватися, то сили електростатичного поля виштовхнуть його за межі своєї дії, внаслі­док чого зменшиться енергія взаємодії зарядів. Теоретично електростатич­не поле поширюється до нескінченності і його сили переміщують вільний заряд на її край. У цьому разі здійснена силами поля робота дорівнюватиме

усій енергії взаємодії зарядів.

Якщо переміщується заряд Є₂, що на початку руху перебував у точці

поля з напруженістю Е₂, то робота сил поля

00 00

00

\FdJ=\E₂Q₂dt^Q₂\E₂dL

2 2 2

Оскільки у точці поля заряд Q₂ визначається утвореним ним скаляр­ним потенціалом ф, то останній можна визначити через напруженість електричного поля

— дф₂ Ei = -grad<p₂ =——,

звідки

cß

Ф₂ = - f Eid і. О

У такому разі здійснена робота з переміщення заряду

00

\Edl^-Q₂y₂,

2

а рівна їй, але протилежна за знаком енергія взаємодії двох зарядів, яка зменшується під час пересування заряду в нескінченність, буде

^_е-0₂Ф2-Те саме стосується і заряду Q_x :

-сю

Рі сій

2 Оскільки нескінченність одна, то повна

₄₎

<3і Од ^ + оо енергія взаємодії двох зарядів (рис. 13.13)

(+У*^г~^~- визначиться, як середнє значення двох

" енергій, тобто

^{1 А} к=\

Уразі, коли силами поля переміщуються «-зарядів, енергія їх спільної взаємодії

Отриманий вираз енергії взаємодії стосується лише точкових зарядів.

13.15. ЕНЕРГІЯ ЕЛЕКТРОСТАТИЧНОГО ПОЛЯ

Якщо електростатичне поле збуджується об'ємними і поверхневими зарядами, то їхні елементарні заряди с!() ^\иІУ та сІО-аіІЯ можна вважа­ти точковими. У цьому разі енергія взаємодії зарядів набере вигляду

к^і^А^А^,

V

в якому складова \ У?-сіУ враховує енергію, накопичену в об'ємі єлектро-

0 ² Л'

статичного поля, а складова [ \ сІБ — енергію, розподілену на поверхні

2

об'єму поля. ⁰

Теоретично межами поля є нескінченно віддалені точки, в яких вектор

напруженості електричного поля ї? = 0, і поверхні провідників, на яких потенціал можна вважати нульовим, тобто (р = 0.

Оскільки розбіжність вектора зміщення електростатичного поля дорів­нює об'ємній густині заряду сііу£>-р, енергію електромагнітного поля можна записати у вигляді

Г_е = ' 1 сііу(₍р А^^А ^ЧУ.

Враховуючи, що за диференціальною формою закону Ґаусса

оЇуХ^р, gгadф = £',

а за теоремою Остроградського—Ґаусса

V 5*

0 0

її можна перетворити до вигляду

⁵ ФЯЛС-^ФР

о ¹ о ¹ о

Порівнюючи другі складові обох виразів енер гії електричного поля

^{"цім „ і"/ /' і,}

\д> о можна стверджувати, що густина електрично­го заряду а на поверхні об'єму дорівнює його електричному зміщенню П.

Оскільки розглядаємо енергію електростатичного поля усередині об'є­му (яка не виходить з нього), то додатну нормаль до поверхні об'єму £ потрібно спрямувати усередину об'єму тобто зробити від'ємною (рис. 13.14). Це дає змогу записати, що

З урахуванням цього енергію електричного поля можна подати у такій формі:

о ¹ о ¹ о

або

Л'

о

^{ікс4 ^і'-і-= = 1 2}

0

Фізично цей вираз означає, що посієм енергії електричних зарядів є електричне поле, причому енергія розподіляється в усьому об'ємі з густи­ною р.

Об'ємна густина енергії електричного поля

г

Якщо напруженість електричного поля Е > 0, то сили поля здатні ви­конати роботу за рахунок енергії поля.

13.16. сили, ЩО ДІЮТЬ В ЕЛЕКТРИЧНОМУ ПОЛІ

Якщо заряджені тіла змінюють своє положення у просторі, то енергія електричного поля також змінюється.

Розглянемо електричне поле заряджених дротів, причому рух зарядів дуже повільний- В такому разі магнітні явища, що супроводжують їхній

рух, можна не враховувати. Рух тіл у полі може здійснюватись як під дією сил'поля, так і під впливом зовнішніх сил. Причому можливі два випадки:

1. електричні заряди дротів під час руху незмінні (Q = const);

2. скалярні потенціали дротів під час руху незмінні (ср = const). Нехай у першому випадку протилежно заряджені дроти ізольовані від

джерела енергії і рухаються (розбігаються, збігаються) завдяки електрич­ному полю на нескінченно малу відстань. У цьому разі поле виконує роботу і енергія його зменшується на dW_G. За законом збереження енергії Ті змен­шення дорівнює роботі сил електричного поля, тобто dW_MQX +dW_c = 0. Якщо дроти зближуються, то їхня ємність

С ---- ze^S/d

зростає на dC, де S — площа максимальної активної поверхні дроту при його перерізі вздовж довжини і відносно сусіднього дроту; d — відстань між поверхнями дротів. Відповідно до зростання ємності напруга на кон­денсаторі або напруга між дротами, яка становить

U=Q/C,

зменшується imdUi відповідно енергія, накопичена у вигляді електрич­ного поля конденсатора, поверхнями якого є дроти, зменшується на

dlY_c=QdU/2.

Оскільки потенціал одного із дротів можна вважати нульовим, то на­пруга між дротами

Через велику кількість зарядів у дротах слід враховувати спільний за­ряд -,'х f^Q_h. У цьому разі робота, виконана силами електричного поля з

переміщення Дротів,

^L /с=1

З рівняння видно, що одночасно зі зменшенням енергії електростатич­ного поля зменшуються потенціали ц>_к усіх п точок поля (за кількістю за­рядів), оскільки зменшення заряду за початковими умовами неможливе (0 = const).

Якщо відповідно до другого випадку робота з переміщення дротів ви­конується зовнішньою силою, то енергія їхнього електростатичного поля зростатиме на розмір зовнішньої енергії

dW^=dW_tAA_Qkdy_k.

^Ак=\

Щоб виконувалась умова і потенціали дротів залишалися незмінни­ми вони мають бути з'єднаними із зовнішнім джерелом живлення. Отри­мана ззовні енергія джерела dW_n має дорівнювати роботі сил електроста­тичного поля, яку витрачено на пересування заряджених дротів, плюс приріст енергії електростатичного поля:

dW^+dW^dW_}V

Якщо заряд /с-го дроту зміниться на величину приросту заряду dQ_k, то енергія, віддана зовнішнім джерелом, становить

Зовнішня енергія, витрачена на нескінченно малу зміну заряду в усіх п точках, визначиться як сума

Як визначено вище, змінепня енергії електростатичного поля в разі п зростання і за умови, що q> = const, становить

Звідси робота зовнішньої сили джерела живлення в електричному полі

dW^dW_A~dW^\dW_lv

Якщо дроти в електричному полі пересуваються без впливу зовнішньо­го джерела живлення, який змінює їхній потенціал dW_)Х = 0, а під дією зовнішньої сили, то рівняння балансу енергії перетвориться на таке:

^zk=\

У цьому разі енергія електростатичного поля дротів зменшиться на ве­личину _/;

-dW_c^-^XY_J^_kdQ_k. ^zk=\

Внаслідок цього при незмінних потенціалах дротів заряд на них збільшиться, виникне напруга і вони стануть здатними віддати енергію

dW_R = dW_mbli + dW_e=~Z y_kdQ_k.

k=l

Силу, що діє на заряджене тіло в електростатичному полі, визначають за виразом

dW_e=±F_ldi,

звідки

Додатному значенню сили відповідають умови ф = const і змінна ємність, а від'ємному — Q- const і змінний потенціал.

13.17. МЕТОДИ РОЗРАХУНКУ ЕЛЕКТРОСТАТИЧНИХ ПОЛІВ

Здебільшого розрахунки електростатичнихполів зводяться до визна­чення напруженості електростатичного поля Е при заданому незмінно­му значенні заряду Q і його розподілу в просторі. Якщо вектор напруже­ності Е неможливо безпосередньо визначити, то спочатку знаходять ска­лярний потенціал його ф і наступним кроком — напруженість Е.

Найпоширеніший метод розрахунку полів — це інтегрування рівнянь поля. Іноді застосовують інші методи: суперпозиції; дзеркальних відобра­жень; що ґрунтується на теоремі Ґаусса; конформних перетворень; гра­фічний та ін.

13.17.1. МЕТОД ІНТЕГРУВАННЯ РІВНЯНЬ ПОЛЯ

Відповідно до рівняння Пуассопа і за умови, що заряди розподілені по об'єму, електростатичне поле описують рівнянням

або, якщо немає зарядів, рівнянням Лапласа

V V- 0.

Під час інтегрування треба використовувати так звані граничні умови, тобто обмеження, які враховують межі області, властивості середовища.

На початку розрахунку характеристик поля у середовищі довільно оби­рають точку нульового потенціалу (ф = 0). В електростатичному полі об'ємного заряду напруженість Е має бути скінченною величиною.

Нехай в однорідне електростатичне поле з напруженістю Ео = const внесено металеву кулю, радіус якої R — а (рис. 13.15). Припустимо, що куля не мала заряду, тобто Q = 0, а відносна діелектрична проникність се­редовища, в якому вона перебуває, становить г. Визначимо, як перероз­поділиться напруженість електростатичного поля Е в середовищі навко­ло кулі.

Оскільки куля найкраще визначається сферичною системою коорди­нат, то її початок розмістимо в центрі кулі. Сферичну координату 0 відра­ховуватимемо за часовою стрілкою відносно напрямку напруженості Ео зовнішнього поля. Виходячи з міркувань симетрії, можна припустити, що

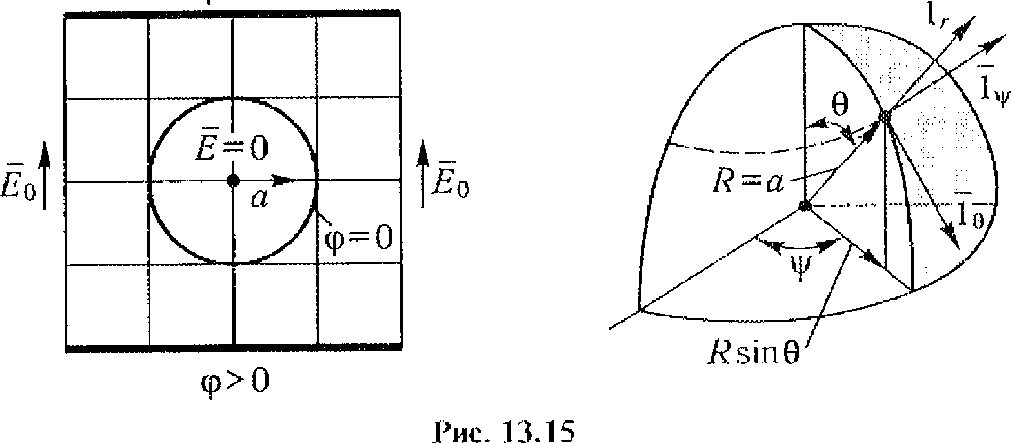
вектор напруженості поля і його скалярний потенціал є функціями сфе­ричних координат R і _0. Як було зазначено вище, напруженість поля все­редині металевої кулі Е = 0. Зовні кулі характер змінений потенціалу мож­на подати у вигляді рівняння Лапласа (джерел заряду в кулі немає) для сферичної системи координат, але з урахуванням симетрії самої кулі вздовж координати \(/ лише відносно двох координат — R, 0 :

гАр 2 о\\> 1 Ар₊ cos 0 Дер ₍₎

Розв'язуючи рівняння, шуканий потенціал подамо у вигляді добутку величин /[(/{) та ./₂(0), тобто як ср - 7j,/₂. Щоб визначити ці величини, підставимо їх у рівняння Лапласа і отримаємо його у такому вигляді:

² OR² ^ _R2 _т2 _R2_sm<K)

R²

Помножимо складові виразу па . :

hh

R²_d²f_{ 2Rdf_{{ =}_ і д²/₂_ _Cose д/₂ J\6R^{2 +} f\<^)R h дд² /₂sin0OO"

Отримане однорідне диференціальне рівняння справедливе для будь-яких значень координат /?, 9.

Припустимо, що кожна складова цього рівняння дорівнюватиме к . Тоді для його правої частини отримаємо вираз, що має тзву рівняння Ле-жандра: ₂

1 д І2 cos 6 d/₂ __fc2

f₂ /₂ sin e ae

розв'язок якого

/₂(G) = cosO.

Причому постійна складова в рівнянні Лежандра набуває значення к = 2. В цьому легко переконатися, якщо здійснити зворотну підстановку. Ліва частина диференціального рівняння з урахуванням того, що

2, становитиме

АГ

дК

Розв'яжемо його заміною змінної. Нехай /?-е^и', тоді звідки

'сі Я

#1

З урахуванням наведеного і того, що змінна у виразі одна, множник

подамо у вигляді

сі/_у _с(/\і1и> _ сі/у сІК сімсНІ сім

Його друга похідна

с

с/\у

ГІ\ сі

сііі'

V

_;-„''/, "і

сім?

_{= с} 2>і^ ^ґ/ "У1 __с 2к

Підставляючи складові загального рівняння в лівий вираз диференці­ального рівняння відносно множника потенціалу /,, отримаємо

,2 Н'

, 2и'^_./] -2и' %_ ² ст

сім'¹

\

2с»\ о

- \

-2./] -0,

або після перетворень

2/^0.

Розв'язок однорідного диференціального рівняння має вигляд експо-нси цій ного виразу

де р_] та р₂ — корені характеристичного рівняння р +/>-2 = 0, а саме

або

_-і±7Г+8

Ріа = ₂

Р₁ = ІР₂=-²-

Таким чином, розв'язок однорідного диференціального рівняння от­римаємо у вигляді

/₁=А₁^ ₊ А₂^^А_ІЯ + А₂ ¹

К

Повний розв'язок рівняння Лапласа відносно розподілу потенціалу навколо кулі, розміщеної в однорідному електростатичному полі, буде

Ф = /і/>

(

A, R + A

І ) ² R² j cosO.

Відповідно вектор напруженості електричного поля

Е = -^гас1(р.

Знайдемо проекції вектора поля Е на осі/?, 0 сферичної системи ко­ординат;

Е

R

9(р cR

^ґ 2 ^

А, + Л₇■ cosO;

v R³)

Е,

дер (

RcO

А₇

А, +—4- sin G.

Для того щоб визначити постійні інтегрування А_х і А₂, скористаємо­ся початковими граничними умовами. Так, з одного боку, при радіусі кулі /? = оо вона не впливає па стан електростатичного поля, а його напру­женість Е = Е{) не змінюється відносно початкового значення. Отже, мож­на записати, що

( 2 >

V

А< +А_п „ cosO = -/1, cost) = £"{) cosO,

² ^

звідки постійна інтегрування Л[ = -Е§.

З другого боку, поверхня кулі є еквіпотенціальною поверхнею і тому при її незмінному радіусі Я=а, але змінній координаті — куті 0 матиме­мо рівняння потенціалу у вигляді

Ф

A,R+A

1

² R² J

яке справедливе для будь-якого значення потенціалу і зокрема при ф = 0. Тоді

А_]а+А₂-\ = 0, а

з — з

звідки постійна інтегрування А₂ = ~А_{а - Е₀а .

Остаточно потенціал в однорідному електростатичному полі з напру­женістю £о в разі розміщення у ньому металевої кулі визначимо так:

{ з А

сойО.

К. к )

Ф=Е₀

(2«³ ^ /7 - р ^ш .1.1

Проекції вектора напруженості поля

со50;

Л₍₎ - Л₀

v ;

2 а

БІПО.

У

Модуль вектора напруженості

З аналізу рівняння напруженості електростатичного поля випливає, що при радіусі металевої кулі Я — а і змінній координаті — куті 0 = 0 вона досягає максимуму:

Загальну картину розподілу скалярпого потенціалу і вектора напруже­ності електростатичного поля для розглянутої задачі наведено нарис. 13.12.

13.17.2. МЕТОД КОМІРОК

Цей метод використовують для приблизного розрахунку будь-якого за характером плоскопарадсльного поля.

Нехай розподіл потенціалу вздовж периметра (' плоскої поверхні (рис. 13.16) відомо. Визначимо потенціали точок всередині площини, об­меженої периметром Р. Згідно з методом нанесемо па поверхню площи­ни квадратну сітку зі стороною комірок а. Довжина сітки пов'язана з точ­ністю розрахунку потенціалу.

У прямокутній системі координат потенціали точок електростатично­го поля визначають згідно з рівнянням Л апласа

^2 л2

£-ї₊а_ї = о.

дх ду"

Позначимо потенціали сусідніх вузлів комірок як ф₀, ф₍, ф₂, Фз, Ф4-Якщо довжина а сторони комірки досить незначна порівняно з обмежу­вальним периметром С, то складові рівняння Лапласа можна визначити так:

сАр _ фі -Фо_„фо~"Фз. ^²ф ~ ^ф2.':⁽^»... ^ф".;:°і

дх¹ а¹ а¹ ду^£ а" а

У

0

х

Рис. 13.16

Підставляючи їх у рівняння Лапласа, отримаємо

щ ~фр 5^111^ 4-2°²^і2^_

1 "' 2 ? 2

а¹ а а* а

(ф! + ф₂ + Фз + ф₄ - 4ф₀ ) = 0.

а

Звідси випливає, що потенціали вузлів сусідніх комірок пов'язані між собою так:

(ф, +ф₂ +Ф3+Ф4 -4<Ро) = °-

Розглянемо приюіад застосування методу. Найпростішу поверхню з відомими значеннями потенціалів вздовж її межі, які, у свою чергу, нале­жать до вузлів цієї межі, наведено нарис. 13.17. Треба визначити потенціали

вузлів ф_т, ф„, ф_р1 Ф₉ ■

На початку розрахунку задамося приблизними значеннями потенці­алів всередині контуру, наприклад

_Фт-160В, <_Рл=120В, ф_/,=80В, ф_д=40В. Застосовуючи рівняння ф| +ф₂+ф₃ + ф₄ -4ф₀ =0 для вузла /я, отри-

маємо

ф^+200 + 200 + ф^бООВ.

Оскільки 4ф„, =640 В, то похибка розрахунку становить А_т =Хф~⁴Ф -40 В.

Аналогічно отримаємо для наступних трьох вузлів:

4

100 +200 +ф_и + ф_? = 500В, Д_л =іф-4_Фи =-20В;

т

4

% +%_п +100 + 0-300 В, А_р =іф-4_Ф/, = -20В;

4

0 + ф„ 4- _Ф, + 0 - 200 В, а₉ = 2ф - 4ф₉ = 40 В.

Наступним кроком корегуємо довільно обрані на першому кроці зна­чення потенціалів внутрішніх вузлів комірок. Для цього похибку у визна­ченні потенціалу кожного вузла ділимо па чотири — за кількості прилеглих до нього вузлів, отримані значення додаємо до значення потенціалу відпо­відного вузла. Тоді

Л л л.. л

"' ... ; 5 В; / - 513; 10 В.

4 4 4 4

Отже, для наступної ітерації потенціали внутрішніх вузлів становлять: _ф;„ ■ - ф_и -і ^Л;' = 160 - і 0 150 В; _Ф;₍ - = 125 В; ф', = 75 В; _Ф;_у ^ 40 В.

Наступну та інші ітерації визначаємо доти, доки отримана похибка розрахунку перевищуватиме бажану.

13.ЇХ. ЕЛЕКТРИЧНЕ ПОЛЕ

У ПРОВІДНОМУ СЕРЕДОВИЩІ

ІЗ. 18.1. СТРУМ 1 ГУСТИНА СТРУМУ ПРОВІДНОСТІ

Якщо у провіднику є електричне поле, то воно зумовлює упорядкова­ний рух зарядів, які є струмом провідності. В металевих провідниках струм провідності визначається рухом електронів.

Мірою струму вважається межа відношення заряду Ад провідника до тривалості його пересування А/ крізь переріз провідника А2> за умови, що тривалість пересування наближується до нуля, тобто

Ад сід і - Іпп —- —-. д/-.>оА/ сіі

Струм, як і заряд, скалярна величина. Якщо значення струму не змі­нюється в часі, то його називають постійним струмом^

Густиною струму називають векторну величину 5, числове значення якої дорівнює межі відношення струму, який тече крізь поверхню, пер­пендикулярну до руху зарядів, до площі цієї поверхні за умови, що вона наближається до нуля, тобто

о ,• Аі сіі

6 = Мт —тг-^"7?г--д^оА^, аї$_п

Одиниця густини струму — ампер на квадратний метр (А/м²).

Напрямок вектора густини струму 5 обирають так, щоб він збігався з напрямком руху позитивних зарядів у провіднику Струм і густина струму пов'язані співвідношенням

Л'_ _

0

При постійному струмі розподіл зарядів вздовж провідника не змі­нюється в пасі. Електричне поле незмінних у часі зарядів збігається з елек­тричним полем нерухомих зарядів. Іноді, ідеалізуючи задачу, розглядають поверхневі струми і їхню густину, А/м, тобто

,. Аі сіі

де І — периметр перерізу провідника.

13.18.2.ДИФЕРЕНЦ1АЛЬНА ФОРМА ЗАКОНУ ОМА В однорідному ізотропному середовищі провідника густина струму провідності 6 пропорційна напруженості його електричного поля Е, а саме

де у — питома провідність провідника, См/м.

Відомо якщо в електростатичне поле внести провідник, то в ньому почнеться'перерозподіл зарядів так, щоб їхнє спільне електричне поле компенсувало дію зовнішнього електростатичного поля, в якому його роз- містили. . - .

Отже щоб у провіднику безперервно протікав струм, необхідне зовнішнє електричне поле, сили якого переміщували б його заряди. Таке поле можна утворити і постійно підтримувати процесами неелектроста-тичного походження (хімічними, термоелектричними та ш.), які мають назву стороннього електростатичного поля.

Під час руху струму в провіднику будуть втрати енергії від стороннього поля які супроводжуються виділенням теплоти з подальшою п віддачею у зовнішнє середовище. Ці втрати мають безперервно поповнюватися від джерела стороннього поля, щоб струм у провіднику не припинявся. Отже, стороннє поле завжди пов'язане з джерелом енергії.

Напруженість стороннього електричного поля дорівнює межі відношен­ня сторонньої сили, що діє на заряд, до заряду, який переносять щ сили, за умови, що кількість заряду, який переноситься, наближується до нуля;

— ^стор Астор = ІШ1

Оскільки провідник має власні заряди й утворене ними власне елек­тричне поле Е, то існуватимуть і електростатичні сили його взаємодії

Рис. 13.18

зі стороннім електричним полем. У цьому разі напруженість сумарного поля

Л сум • Л + /істор ■

Лінійний інтеграл напруженості стороннього поля /істор між двома точками (а\Ь) заданого шляху АС (рис. 13.18) називають електрорушійною силою:

^Ca\h " j ^стор^/Г 0

Якщо шлях інтегрування замкнений, то електрорушійну силу назива­ють діючою у контурі

е

е-с[>Л'стор</ С.

Оскільки

І' crop

о .. і У ЛУ

де. у, S —- питома провідність і переріз провідника, то ЕРС, що діє в кон­турі, можна подати у вигляді

і id? id?, е -- (р =/ф ^ ,

о $У 0 ^ЛТ

який називають другим правилом Кірхгофа в інтегральній формі.

Лінійний інтеграл напруженості підсумкового поля називають напру­гою вздовж контуру інтегрування або падінням напруги на ділянці кола

alb

"alb ⁼ \ ^^wdl. 0

Як видно, напруга та ЕРС залежать від обраного шляху інтегрування. Відомо, що в електростатичному полі інтеграл напруженості вздовж замк­неного контуру дорівнює нулю:

§Ed£ = 0,

о

а її лінійний інтеграл не залежить від шляху інтегрування і визначається різницею потенціалів на його початку і кінці:

Ь_

\Edt-=<$_a-<$_b.

а

Зв'язок між напругою, різницею потенціалів та ЕРС визначають за рівнянням _{аХЬ Q[b аІЬ}

} Ecyndt= \ Edl + \ EcTopdC, 0 о 0

з якого випливає, що

Якщо шлях інтегрування замкнений, то

j>Edl = 0 0

і напруга вздовж замкненого контуру вже визначиться як друге правило Кірхгофа в інтегральній формі:

^f_

и - j Есуud І = § Ecropd f = e.

о о

Тобто для миттєвих значень величин алгебрична сума падінь напруги в замкненому контурі дорівнює електрорушійній силі, що діє в контурі.

На тих ділянках провідника, де є сторонні сили, закон Ома у диферен­ціальній формі має вигляд

8 = у Е_Сум - У (Е + Естор ), придатний як для постійного, так і для синусоїдного струмів.

ІЗ 18 З ДИФЕРЕНЦІАЛЬНА ТА ІНТЕГРАЛЬНА ФОРМИ ЗАКОНУ ДЖОУЛЯ-ЛЕНЦА

Потужність теплових втрат у провіднику

Р=Ш.

Якщо розглянути елементарний об'єму dVпровідникового матеріалу замкненого електричного кола (рис. 13.19), то

втрати потужності у вигляді теплоти, що відда- ^* —

ється зовнішньому середовищу, становлять ^ А- 7^і

dP = dIdU =bdSEdt^bEdV. I ^dV

Звідси об'ємну густину втрат теплоти, або диференціальну форму закону Джоуля—Ленца, Рис. 13.19

визначають так: ,

аУ у

або в інтегральній формі

V

Р=\уЕ²с/У. 0

13.18.4.ДИФЕРЕНЦ1АЛЬНА ФОРМА ПЕРШОГО ПРАВИЛА КІРХГОФА

Розглянемо замкнену поверхню 5(рис. 13.20), що охоплює вузол елек­тричного кола, до якого по гілках втікають струми /], /₂ та витікають

/₃, /₄. Вважаючи додатну нормаль спрямованою зовні від замкі іеної по­верхні, за першим правилом Кірхгофа можна записати

Л^+/2

де струми

о о о о

або

.У, -ьї₄

о

Оскільки поза межами поперечних перерізів гілок 3^, Л"₄

густини струму немає, тобто 6 - 0, то інтеграл по окремих перерізах гілок

можна замінити інтегралом по всій по­верхні 5, що їх охоплює:

$5^ = 0.

0

Таким чином, перше правило Кірхгофа у диференціальній формі дістає таке визна­чення: потік вектора густини струму крізь замкнену поверхню дорівнює нулю, тобто

сііуб = 0.

Рис. 13.20

Фізичним поясненням цього є те, що заряд, який входить до будь-якого об'єму, дорівнює заряду, який виходить з нього за той самий проміжок часу. Тобто постійний за напрямком струм — безперервний у часі, а лінії його густини замкнені самі на себе через зов­

нішнє електричне коло. Постійний струм у будь-яких перерізах нерозга-лужсного кола має незмінне значення, інакше були б ділянки кола, на яких заряд накопичувався б або зменшувався, що неможливо.

Слід пам'ятати, що в електричних колах змінного струму, якщо в них є конденсатор, сііуб ф 0, оскільки на них накопичуються електричні заря­ди, які створюють електричне поле.

13.18.5. ПОВНИЙ ЕЛЕКТРИЧНИЙ СТРУМ

Електричний струм у провідному середовищі визначається як спрямо­ваний рух електричних зарядів під дією сили зовнішнього поля і має на­зву струму провідності.

Густина струму провідності пов'язана з напруженістю зовнішнього електричного поля законом Ома

5 = у Е.

Якщо заряди рухаються в непровідному середовищі або у вакуумі зі швидкістю V, то вони створюють так званий струм перенесення. Його гус­тина пропорційна об'ємній густині заряду р і залежить від швидкості пе­ренесення

5_пф=р?>.

У молекулах діелектрика, який вносять в електричне поле, під дією сил цього поля та його напруженості зв'язані заряди починають пересуватися і створюють струм поляризації. Густина струму поляризації пропорційна швидкості змінення вектора поляризованості /;:

З Л^Р-поляр ^ '

Для середовища, в якому поляризованість пропорційна напруженості електричного поля, тобто

р = є₀к_сЕ,

де к₀ — електрична сприйнятливість діелектрика, густина струму поля­ризації визначається рівнянням

^поляр - ^є0^Л;е Qf ■

Усі три струми: струм провідності у провідниках, струм перенесення у вигляді руху зарядів через ізольоване середовище та струм поляризації є рухом електричних зарядів. Кожний із названих струмів супроводжується появою магнітного поля.

Дж. Максвелл запропонував припущення, що електричний струм — це змінення в часі електричного поля у вакуумі, оскільки в цьому разі та­

кож утворюється магнітне поле. І цьому виду струму він дав назву струму зміщення у вакуумі, густина я кого

^й0зм ^_е0 ^

Його відмінність від інших струмів у тому, що він не спричинює у ва­куумі втрат енергії у вигляді теплоти.

Струм провідності з густиною 5 і струм перенесення з густиною 8_пср

наявні яку постійних, так і в змінних за часом електричних полях. Стру­ми поляризації з густиною 5_пояяр і зміщення з густиною 5_0зм наявні лише в змінних за часом електричних полях. Отже, електричний струм — це два різного роду явища — рух електричних зарядів та змінений електричного поля у часі. Основною властивістю будь-якого струму є його властивість збуджувати магнітне поле.

Повним струмом називають сукупність усіх явищ, при яких збуджується магнітне поле. Густина повного струму

У цьому виразі струми поляризації та зміщення об'єднують в один струм, який називають струмом зміщення у діелектрику. Густину його визна­чають так:

~ х (\ ь \ д Я - дЕ ОО

Струм зміщення має властивість текти у діелектрику так само, як струм провідності у провіднику

У подальшому струмом перенесення будемо нехтувати, зважаючи на його мализпу. Тому густина повного струму

Повний струм може виникати як у провідниковому середовищі з не­змінним електричним полем уЕ, так і в непровідниковому середовищі в

д Е

разі змтення в ньому електричного поля є_а ----­У провідниковому середовищі струм провідності значно більший, НІЖ струм зміщення:

У діелектрику з незначними втратами — навпаки:

г ^ ^дЕ і а _ді

Допущення Дж. іМаксвеллапро те, що в діелектрику збуджуються стру­ми зміщення є_я ---- подібно до того, як у провіднику — струми про-ся

відності, пояснює той факт, що електричні пристрої здатні випромінюва­ти у простір енергію, яка поширюється в діелектрику разом з електро­магнітними хвилями.

13.18.6.ДИВЕРГЕНЦІЯ ГУСТИНИ СТРУМУ ПРОВІДНОСТІ

Постійний струм виникає лише у замкненому електричному колі. Лінії вектора густини постійного струму неперервні, а тому

сііу 5 = 0.

Протікаючи крізь довільну замкнену поверхню, постійний струм зав­жди має дорівнювати нулю, оскільки заряд в об'ємі, обмеженому цією поверхнею, при постійному струмі не змінюється.

Змінні у часі струми можуть бути в незамкнених електричних колах, якщо в них є конденсатор. Отже, при змінних у часі електричних полях електричні кола можна виконувати незамкнепими. На тих ділянках їх, де закінчуються лінії густини струму провідності, можуть накопичуватися заряди, тобто вектор густини струму провідності через замкнену поверх­ню може бути більшим від нуля.

Нехай у замкненому об'ємі V, обмеженому поверхнею є електрич­ний заряд дз об'ємною густиною р. Якщо через поверхню б'витікає струм провідності /-&У, то заряде/, який ним переноситься, зменшується і для струму можна записати

. дд

¹ = - А ■

ді

Позначивши струм через його густину, отримаємо струм, що витікає через усю поверхню, у вигляді

_І'ш=-д?і

о <*

V

де заряд, що переноситься, пропорційний його об'ємній густині: д = \ рсІУ.

0

Враховуючи теорему Остроградського, згідно з якою циркуляція вектора густини струму крізь замкнену поверхню дорівнює його розбіжності по об'єму

о о

струм, що витікає через усю поверхню, отримаємо у вигляді виразу

V - V

о ^СІ о

^аб° _г „ др

Тобто дивергенція густини струму провідності дорівнює швидкості спа­дання густини об'ємних зарядів.