3.3. Производные от коэффициентов подъёмной силы и продольного момента изолированных несущих поверхностей по углу атаки при

Как уже упоминалось выше, при расчёте аэродинамических характеристик несущих поверхностей, установленных на ЛА, необходимо учитывать их интерференцию с корпусом, а также с другими несущими поверхностями.

Обширные теоретические и экспериментальные исследования посвящены изучению обтекания и получению аэродинамических характеристик изолированных несущих поверхностей. Большинство теоретических методов разработано для тонких несущих поверхностей. Наиболее общей расчётной схемой, моделирующей обтекание изолированной несущей поверхности при дозвуковых скоростях, является её замена вихревой поверхностью. В основе теоретических исследований несущих поверхностей при сверхзвуковых скоростях лежат нелинейные дифференциальные уравнения газовой динамики. Здесь для расчёта обтекания наиболее разработанными являются методы Е. А. Красильщиковой, Аккерета и теория конических течений.

Как показывают эти исследования, производная от коэффициента подъёмной силы по углу атаки и положение фокуса изолированной несущей поверхности зависят от числа и формы поверхности в плане. Однако при дозвуковых и особенно при трансзвуковых скоростях эти параметры зависят также от формы профиля и, в частности, от его относительной толщины. Используя параметры подобия для изолированной несущей поверхности, можно записать

, . (3.18)

Графики этих зависимостей для приведены на рис. 3.3 [8].

Так как сужение несущей поверхности мало влияет на величину производной , то параметр на графиках не показан, а приведенные данные являются осреднёнными для различных значений сужения. На режимах течения, при которых кромки несущей поверхности переходят от дозвукового типа обтекания к сверхзвуковому, теоретические расчёты указывают на наличие изломов в поведении кривых . На приведенных графиках эти изломы сглажены в соответствии с экспериментальными данными.

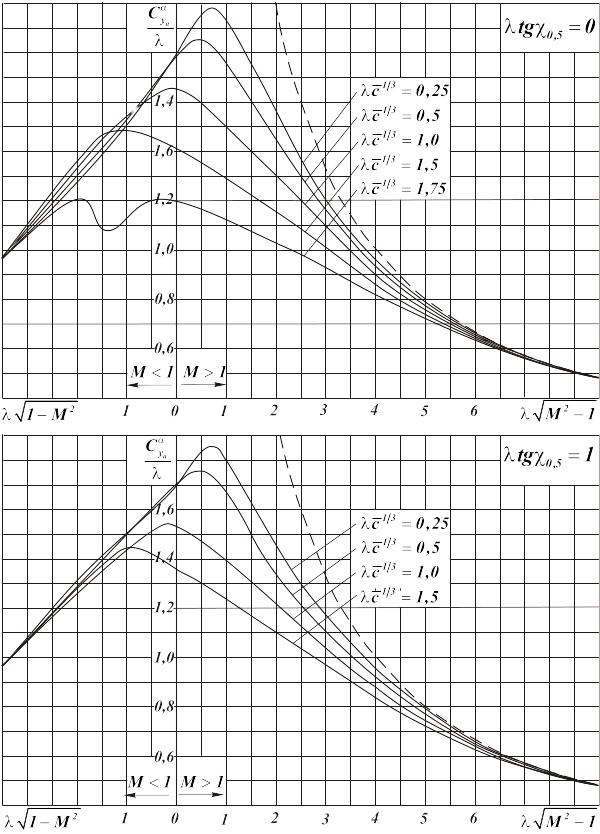
Рис. 3.3. Графики для расчёта несущих поверхностей

Рис. 3.3. Окончание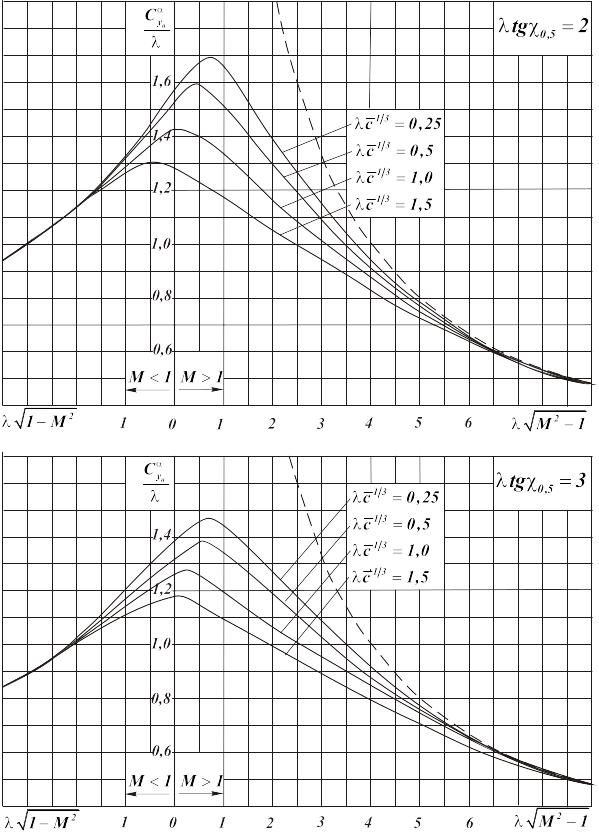

В дозвуковом потоке при больших значениях приведенного удлинения для определения можно использовать формулу

, (3.19)

где – отношение полупериметра кромок несущей поверхности к её размаху. Для поверхности с прямолинейными передними и задними кромками и с концевой хордой, параллельной бортовой,

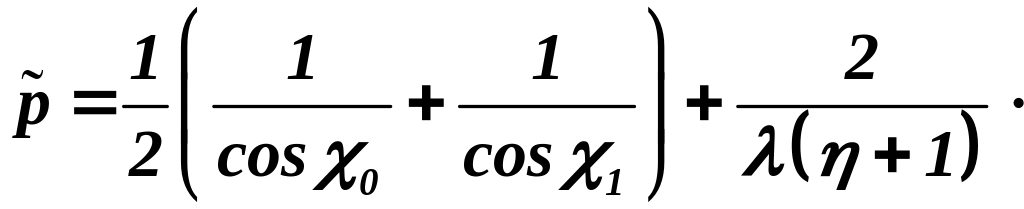(3.20)

С учётом сжимаемости необходимо пользоваться следующей формулой [13]:

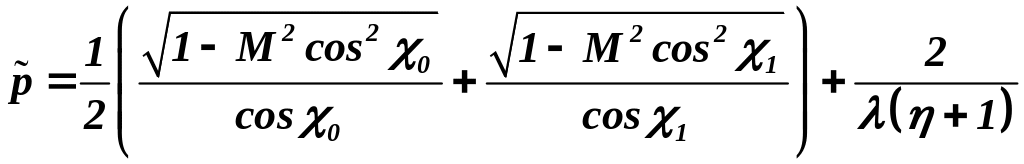. (3.21)

В приведенных формулах и – углы стреловидности передней и задней кромок поверхности.

В сверхзвуковом потоке при больших значениях приведенного удлинения величина слабо зависит от формы поверхности в плане и приближается к аналогичному значению для профиля, т. е.

(3.22)

Эти значения показаны на рис. 3.3 пунктиром.

Линейная теория крыльев конечного размаха позволяет рассчитать положение их фокуса при дозвуковых и сверхзвуковых скоростях. Скорректированные экспериментальными данными результаты для плоских крыльев с симметричными профилями приведены на рис. 3.4. Здесь координата фокуса отнесена к центральной или бортовой хорде поверхности, составленной из консолей, и отсчитывается от её начала. Следует помнить, что эти графики в околозвуковой области имеют качественный характер, так как из-за недостатка экспериментальных данных пока не удаётся выяснить влияние параметра на положение фокуса в этой области. Некоторые данные о влияние этого параметра на положение фокуса прямоугольных крыльев в трансзвуковой области приведены в работе [8]. Кривые, представленные на графиках, соответствуют значениям .

Рис. 3.4. Графики для расчёта координаты фокуса изолированных несущих поверхностей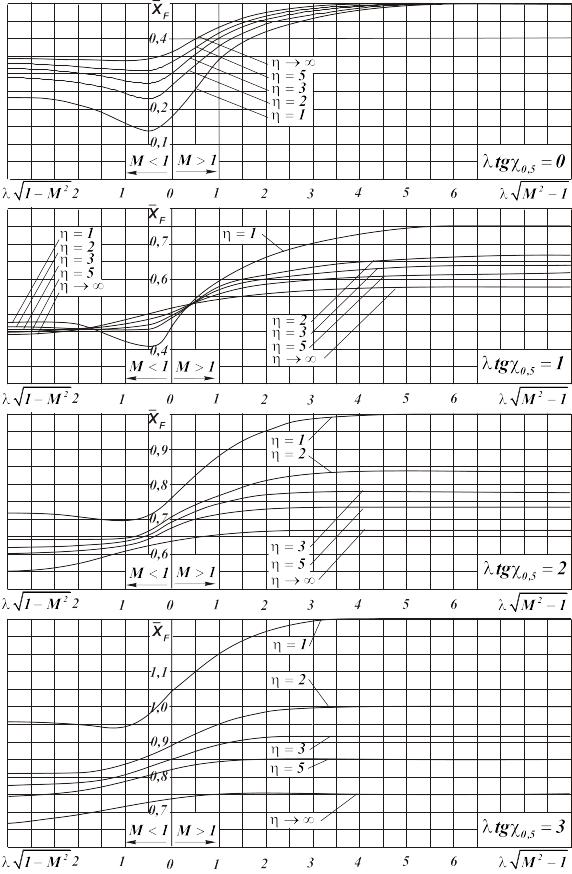

Положение фокуса несущей поверхности для дозвуковых скоростей при больших значениях приведенного удлинения можно приближённо определить по формуле [13]

, (3.23)

где – фокус профиля.

В сверхзвуковом потоке при больших значениях приведенного удлинения координата фокуса поверхности стремится к положению центра тяжести площади поверхности в плане:

. (3.24)

Здесь и , где – величина средней аэродинамической хорды; – величина бортовой хорды; – расстояние между началами бортовой и средней аэродинамической хордами.

Найденные величины позволяют определить производную от коэффициента продольного момента несущей поверхности по углу атаки:

, (3.25)

где – расстояние от носика части ЛА до начала бортовой хорды рассматриваемой поверхности.

Аэродинамические характеристики несущих поверхностей определяются с учётом торможения потока, т. е. .