2.5.3. Коэффициент волнового сопротивления несущих поверхностей

Волновое сопротивление несущих поверхностей, как и других частей летательного аппарата, возникает при . Однако систематические исследования имеются только при сверхзвуковых скоростях полёта, т. е. при . При необходимости волновое сопротивление несущих поверхностей в трансзвуковом диапазоне чисел можно определить по следующей приближенной формуле [13]:

. (2.49)

Здесь – угол стреловидности по линии максимальных толщин; – критическое число ; – число , соответствующее максимальному значению коэффициента волнового сопротивления при околозвуковых скоростях,

. (2.50)

При сверхзвуковых скоростях полёта коэффициент волнового сопротивления несущей поверхности согласно линеаризованной теории зависит от числа , формы поверхности в плане, а также от относительной толщины и формы профиля. Форма трапециевидной поверхности характеризуется удлинением , сужением и стреловидностью по любой линии -частей хорд. Число независимых переменных можно значительно уменьшить, введя обобщённые параметры. В этом случае можно записать

.

На рис. 2.9 и 2.10 представлены графики этих значений для трапециевидных крыльев с ромбовидным профилем [8]. Они соответствуют определённым значениям сужения: , и . При увеличении числа , или, точнее, приведенного удлинения , влияние формы несущей поверхности уменьшается. Это можно объяснить сужением конусов Маха (при увеличении числа ), выходящих из точек излома передней кромки и из передних точек боковых кромок.

Рис. 2.9. Графики для расчёта коэффициента волнового сопротивления несущей поверхности с ромбовидным профилем ( и )

Рис. 2.10. Графики для расчёта коэффициента волнового сопротивления несущей поверхности с ромбовидным профилем при

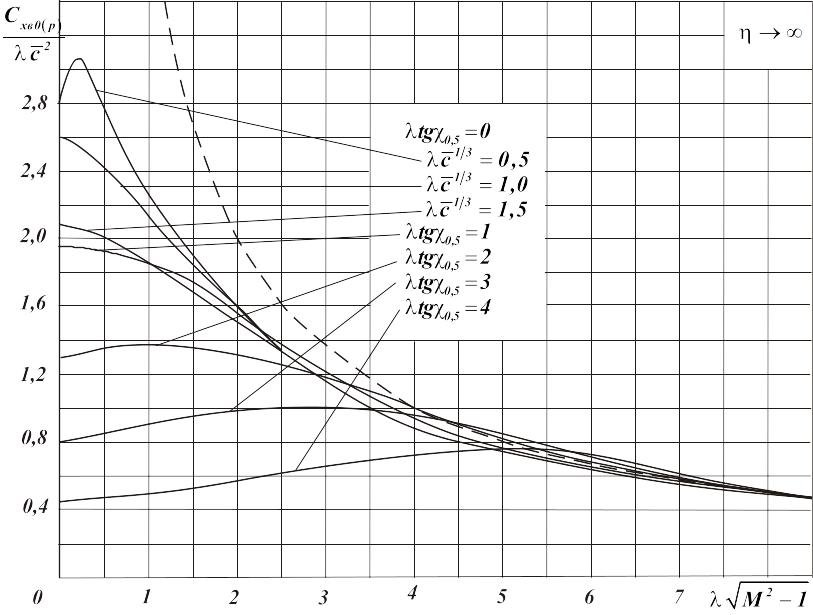
Поэтому при больших значениях приведенного удлинения ( ) коэффициент волнового сопротивления поверхности с ромбовидным профилем может быть определён по формуле

, (2.51)

как для профиля (крыла бесконечного размаха).

Следует отметить, что экспериментальные значения коэффициента волнового сопротивления заметно расходятся с теоретическими особенно в областях, где теоретические кривые имеют резко выраженные пики. Здесь для определения волнового сопротивления линейная теория неприменима. Максимального значения коэффициент волнового сопротивления достигает тогда, когда линия максимальных толщин переходит с дозвукового обтекания к сверхзвуковому (по линейной теории). Однако если при это происходит действительно при , то при увеличении сужения этот максимум смещается к меньшим значениям приведенного удлинения, т. е. при . В этом случае смещение тем больше, чем больше сужение поверхности.

При больших значениях приведенного удлинения , когда линия максимальных толщин становится существенно сверхзвуковой, т е. при , схожесть теоретических значений с экспериментальными значительно лучше, но всё же и здесь теоретические значения волнового сопротивления несколько завышены. Это можно объяснить тем, что поток за точкой максимальной толщины расширяется не полностью из-за наличия пограничного слоя, что приводит к повышению давления в этой области, а следовательно, и к уменьшению волнового сопротивления. Так, например, исследование ромбовидных профилей в аэродинамической трубе показывают, что экспериментальные данные меньше теоретических приблизительно на 13%.

Следует иметь в виду, что при малых сверхзвуковых скоростях полёта коэффициент волнового сопротивления также зависит от параметра трансзвукового подобия . Однако приведенные данные позволяют учесть это влияние только для . Для приближенного определения коэффициента волнового сопротивления в этом диапазоне чисел полёта можно воспользоваться формулой (2.49).

Графики, полученные для поверхностей с ромбовидным профилем, могут быть использованы для определения волнового сопротивления поверхности с произвольным профилем.(имеются в виду профили с конфигурацией, характерной для скоростных манёвренных ЛА).

Влияние формы профиля на волновое сопротивление профилей (прямых крыльев бесконечного размаха) в настоящее время хорошо изучено теоретически и экспериментально. Очень эффективным оказалось введение коэффициента , представляющего отношение коэффициента волнового сопротивления данного профиля к аналогичному коэффициенту ромбовидного профиля , т. е. .

Влияние формы профиля на волновое сопротивление крыльев конечного размаха оказывается несколько иным. Анализ экспериментальных данных показывает, что при , т. е. когда линия максимальных толщин дозвуковая, форма профиля незначительно влияет на волновое сопротивление. При существенно сверхзвуковой линии максимальных толщин ( ) влияние формы профиля на коэффициент примерно такое же, как и для профиля. Если эта линия сверхзвуковая (т. е. при ), то, следуя методике, изложенной в работе [8], коэффициент волнового сопротивления несущей поверхности с произвольным профилем можно представить в следующем виде:

, (2.52)

г

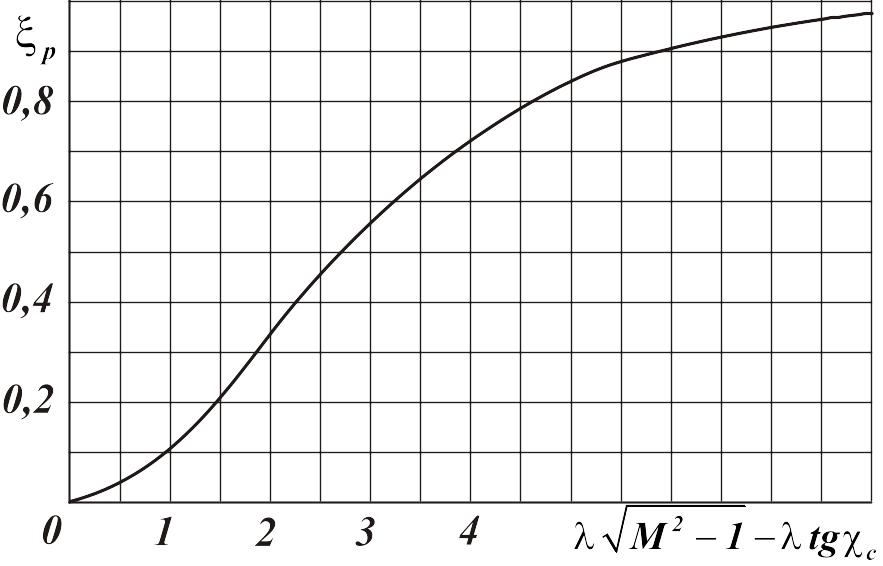
Рис. 2.11. График функции для расчета волнового сопротивления поверхностей с произвольным профилем

де множитель находится с помощью графика на рис. 2.11, коэффициент – с помощью графиков на рис. 2.9 (в зависимости от параметров поверхности), коэффициент определяется по таблице, приведенной в прил. 2. Это позволяет воспользоваться приведенными графиками для широкого класса профилей.

Значение множителя можно также приближенно определить по следующей формуле [8]:

. (2.53)

При увеличении значений разности влияние формы профиля на коэффициент волнового сопротивления возрастает. При существенно сверхзвуковой линии максимальных толщин ( ) влияние формы профиля на коэффициент волнового сопротивления несущей поверхности примерно такое же, как и для профиля (прямоугольного крыла бесконечного размаха).

Необходимо иметь в виду, что при вычислении коэффициентов волнового сопротивления несущих поверхностей в формулы должны быть подставлены геометрические параметры соответствующих поверхностей и числа с учётом коэффициента торможения потока ( ).