
- •Лекция 1 п редмет и метод термодинамики
- •Термодинамическая система
- •Термодинамические параметры состояния
- •Уравнение состояния
- •Термодинамический процесс
- •Теплоемкость газов
- •Лекция 2 Смеси идеальных газов
- •Аналитическое выражение первого закона термодинамики
- •Лекция 3 Внутренняя энергия
- •Работа расширения
- •Теплота
- •Энтальпия
- •Энтропия
- •Лекция 4 Общая формулировка второго закона термодинамики
- •Обратный цикл Карно
- •Изменение энтропии в неравновесных процессах
- •Лекция 5 Термодинамические процессы идеальных газов в закрытых системах
- •Так как для политропы в соответствии с (5.1)
- •Эксергия
- •Лекция 6 Термодинамические процессы реальных газов
- •Уравнение состояния реальных газов
- •Лекция 7 Уравнение первого закона термодинамики для потока
- •Истечение из суживающегося сопла
- •Основные закономерности течения газа в соплах и диффузорах
- •Разделив уравнение на pv, найдем
- •Расчет процесса истечения с помощью h,s-диаграммы
- •Дросселирование газов и паров
- •Лекция 8 Термодинамическая эффективность циклов теплосиловых установок
- •Циклы поршневых двигателей внутреннего сгорания
- •Циклы газотурбинных установок
- •Циклы паротурбинных установок
- •Цикл Ренкина на перегретом паре
- •Термический кпд цикла
- •Общая характеристика холодильных установок
- •Цикл паровой компрессионной холодильной установки
- •Лекция 9 Основы теории теплообмена
- •Основные понятия и определения
- •Теория теплопроводности Закон Фурье
- •О t днослойная плоская стенка
- •Многослойная плоская стенка
- •Однородная цилиндрическая стенка
- •Многослойная цилиндрическая стенка
- •ЛекцИя 10 Теплопередача
- •Плоская стенка
- •Цилиндрическая стенка
- •Интенсификация теплопередачи
- •Тепловая изоляция
- •Задачи по теплопередаче
- •Лекция 11 Конвективный теплообмен (теплоотдача) Основной закон конвективного теплообмена
- •Пограничный слой
- •Числа подобия
- •Массообмен
- •Числа подобия конвективного массообмена
- •Лекция 12 Частные случаи конвективного теплообмена Поперечное обтекание одиночной трубы и пучка труб
- •Лекция 13 Описание процесса излучения. Основные определения
- •Теплообмен излучением системы тел в прозрачной среде
- •Перенос лучистой энергии в поглощающей и излучающей среде
- •Лекция 14 Теплообменные аппараты Типы теплообменных аппаратов
- •Расчетные уравнения
- •Лекция 15 Термодинамический анализ топливосжигающих устройств
- •Полезная тепловая нагрузка печи
- •Расчет процесса горения топлива в печи
- •Тепловой баланс печи. Коэффициент полезного действия. Расход топлива
- •Лекция 16 Котельные установки. Общие сведения
- •Устройство парового котла
- •Тепловой баланс парового котла. Коэффициент полезного действия
- •Лекция 17 Состав и основные характеристики жидкого топлива
- •Состав и основные характеристики газообразного топлива
- •Теплота сгорания топлива
- •Количество воздуха, необходимого для горения. Теплота “сгорания” воздуха
- •Объемы и состав продуктов сгорания
- •Лекция 18 Вторичные энергоресурсы Классификация вэр
- •Установки для внутреннего теплоиспользования
- •Котлы-утилизаторы
- •Список использованных источников
Изменение энтропии в неравновесных процессах
Рассмотрим принципиальные отличия неравновесных процессов от равновесных на примере расширения газа в цилиндре под поршнем, получающего теплоту от источника с температурой T1 и совершающего работу против внешней силы Р, действующей на поршень.
Расширение
будет равновесным только
в случае, если температура газа Т
равна
температуре источника (Т=Т1),
внешняя сила
Р равна
давлению газа на поршень (P=pF)
и при
расширении газа
нет ни внешнего, ни внутреннего трения.
Работа расширения газа в этом случае
равна
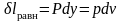 ,
а
изменение энтропии
рабочего тела в таком процессе
,
а
изменение энтропии
рабочего тела в таком процессе
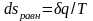 .
.
Невыполнение
хотя бы одного из указанных
условий делает расширение газа
неравновесным.
Если неравновесность вызвана
трением поршня о стенки цилиндра,
то работа
,
совершаемая против внешней силы Р,
оказывается меньше, чем pdv,
так как часть
ее затрачивается на преодоление
трения и переходит в теплоту
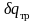 .
Она воспринимается газом вместе с
подведенной теплотой q,
в
результате чего возрастание энтропии
газа в
неравновесном процессе
.
Она воспринимается газом вместе с
подведенной теплотой q,
в
результате чего возрастание энтропии
газа в
неравновесном процессе
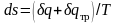 оказывается
больше,
чем в равновесном при том же количестве
подведенной от источника теплоты
.
оказывается
больше,
чем в равновесном при том же количестве
подведенной от источника теплоты
.

Если неравновесность вызвана отсутствием механического равновесия (P<pF), поршень будет двигаться ускоренно. Быстрое движение поршня вызывает появление вихрей в газе, затухающих под действием внутреннего трения, в результате чего часть работы расширения опять превращается в теплоту . Работа против внешней силы снова получается меньше, а возрастание энтропии — больше, чем в равновесном процессе с тем же количеством теплоты .
Если
неравновесность вызвана теплообменом
при конечной разности температур
(температура газа Т
меньше
температуры
источника T1),
то возрастание энтропии
рабочего тела
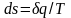 оказывается
больше, чем
оказывается
больше, чем
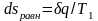 в
равновесном процессе из-за снижения
температуры
газа. При том же положении поршня, т.
е. заданном удельном объеме v,
меньшей
температуре газа соответствует
меньшее его давление р.
Соответственно
меньше должна быть и уравновешивающая
сила Р':
Р'=p'F<P=pF.
Работа
расширения против этой силы
в
равновесном процессе из-за снижения
температуры
газа. При том же положении поршня, т.
е. заданном удельном объеме v,
меньшей
температуре газа соответствует
меньшее его давление р.
Соответственно
меньше должна быть и уравновешивающая
сила Р':
Р'=p'F<P=pF.
Работа
расширения против этой силы
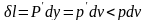 .
.
Итак, неравновесность всегда приводит к увеличению энтропии рабочего тела при том же количестве подведенной теплоты и к потере части работы. В общем виде это можно записать следующим образом:
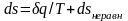 ;
;
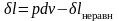 ,
,
Причем
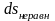 и
и
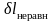 всегда положительны.
всегда положительны.
Ранее было показано,
что для равновесных
процессов справедливо соотношение
.
Разобранный
пример достаточно
наглядно показывает, что в неравновесных
процессах
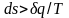 ,
если
—
количество подведенной к системе или
отведенной от нее теплоты, а T
— температура
источника теплоты. Обе записи
являются аналитическими выражениями
второго закона термодинамики:
,
если
—
количество подведенной к системе или
отведенной от нее теплоты, а T
— температура
источника теплоты. Обе записи
являются аналитическими выражениями
второго закона термодинамики:
— в равновесных процессах;
— в неравновесных процессах.
Для изолированных
систем, которые по
определению не обмениваются теплотой
с окружающей средой
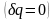 ,
эти выражения
приобретают вид
,
эти выражения
приобретают вид
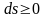 .
.
Если в адиабатно-изолированной системе осуществляются равновесные процессы, то энтропия системы остается постоянной.
Самопроизвольные (а значит, и неравновесные) процессы в изолированной системе всегда приводят к увеличению энтропии. Это положение представляет собой наиболее общую формулировку второго начала термодинамики для неравновесных процессов, известную под названием принципа возрастания энтропии.
Следует подчеркнуть, что последнее неравенство применимо только к изолированным системам. Если от системы отводится теплота, то ее энтропия может убывать, однако суммарное изменение энтропии системы и энтропии внешних тел всегда положительно (либо равно нулю, если в системе протекают равновесные процессы).
Когда изолированная система находится в состоянии с максимальной энтропией, то в ней не могут протекать никакие самопроизвольные процессы, потому что любой самопроизвольный процесс неравновесен и сопровождается увеличением энтропии. Поэтому состояние изолированной системы с максимальной энтропией является состоянием ее устойчивого равновесия, и самопроизвольные процессы могут протекать в изолированной системе лишь до тех пор, пока она не достигнет состояния равновесия.
