Гравиразведка
Гершанок Валентин Александрович
Лекция 1
Фигура Земли и геодезические задачи гравиметрии
Гравиразведка это применение гравиметрии в геологии. Гравиметрические данные широко используются не только для решения геологических задач, но и для решения некоторых геодезических задач, в частности, для изучения фигуры Земли.
Основные и вспомогательные поверхности
Фигурой Земли считается геоид – это тело, ограниченное уровенной поверхностью силой тяжести. Часто под геоидом понимают не само тело, а его поверхность. Геоид – это поверхность, совпадающая со средним уровнем воды в океане, это так называемый, морской геоид. Земной геоид – средний уровень континентов протягивается через океаны. Поскольку определение геоида связано с определением силы тяжести, то изучение фигуры земли – это задача гравиметрии. Геоид – это очень сложная поверхность и выразить ее аналитической формулой очень сложно, поэтому для изучения геоида прибегают к близким по форме поверхностям, в частности, фигурой Земли считают трехосный эллипсоид вращения. Такой эллипсоид называют общим или земным эллипсоидом. Такой эллипсоид должен удовлетворять следующим требованиям:
1. центр должен совпадать с центром геоида;
2. объемы должны быть равны;
3. оси должны совпадать;
4. сумма квадратов отклонений от поверхности должна быть минимальной.
В идеале такой земной эллипсоид не найден, и вообще он не может быть найден. Поэтому задача геодезистов – искать такой эллипсоид. Поскольку эллипсоид не найден, поэтому на практике прибегают к референц-эллипсоиду, который близко совпадает с общим эллипсоидом, лишь на некотором ограниченном участке поверхности. А на других участках он вообще не удовлетворяет никаким критериям.
Форма этих поверхностей определяется методом последовательных приближений. Допустим, зная две из них, определяют другую. Физическая поверхность Земли определяется с помощью топографических измерений, путем нивелирования. Поверхность геоида определяется по гравиметрическим наблюдениям, т.е. по аномалиям силы тяжести и с помощью них определяются высоты относительно поверхности общего эллипсоида. А поверхность общего из эллипсоида определяется по астрономическим наблюдениям. В России за рефернц-эллипсоид принимается эллипсоид Кроссовского. Исходным пунктом этого эллипсоида является обсерватория в Пулково (под Санкт-Петербургом), там поверхности референц-эллипосоида и геоида совпадают.
Определение отклонения (ундуляции) геоида от общего эллипсоида
Пусть W
– потенциал некоторой «идеальной»
Земли, т.е. Земля полностью однородная,
не имеющая никаких аномальных масс; T
– возмущающий потенциал, обусловленный
наличием возмущающих (аномальных) масс.
Уравнение идеального геоида: 
,
а уравнение реального геоида 
.
Δn – приращение по нормали, отклонение геоида от эллипсоида; γ – нормальное значение силы тяжести.
Формула 1.1 носит название формулы Брунса (немецкого геодезиста), она показывает, что для нахождения ундуляции надо знать возмущающий потенциал
Определение возмущающего потенциала
Возмущающий потенциал можно определить двумя способами:
1. Определение T по формуле Стокса:
S(ψ) – функция Стокса, ψ – сферическое расстояние. Т.е. для определения нужно знать силу тяжести на поверхности всей Земли. Поскольку большая часть Земли – это океаны, то измеренные значения силы тяжести распределены крайне неравномерно. Интегрирование идет по поверхности сферы, если интегрировать по поверхности эллипсоида, то формула существенно усложниться.
Если поверхность считать плоской тогда формула Стокса упрощается:
Первые изучения возмущающего потенциала проводились в 30-х годах XX века финскими геодезистами, результаты показали, что отклонение составляет 180 м, для Европейской части отклонение составило около 40 м.
2. Определение при помощи сферического гармонического анализа. Аномальное поле можно представить функцией географических координат:
Где λ, ϕ – координаты Pnm – полином Лежандра.
Если мы точно определяем коэффициенты А и В, то в любой точке земного шара можно узнать Δg вычислительным путем, без измерений (точность 5 мГал).
Сопоставляя эти два способа, мы можем сказать, что формула Стокса более точно учитывает особенности ближнего аномального поля, т.е. если это поле определено очень точно и хорошо, то лучше пользоваться формулой Стокса.
Регуляризация Земли
Вся математическая теория в гравиметрии базируется на том, что уровенная поверхность включает в себя все притягивающие массы, т.е. аномальные массы сосредоточены внутри уровенной поверхности, вне ее аномальных масс нет. В действительности физические массы могут выступать за уровенную поверхность. Потенциал силы тяжести является гармонической функцией только для внутренних точек, поэтому необходимо, чтобы все массы лежали внутри уровенной поверхности. «Удаление» всех выступающих масс внутрь уровенной поверхности называют регуляризацией Земли.
При регуляризации должны быть выполнены следующие условия:
1) Вне геоида не должно остаться масс;
2) Центр геоида не дожжен сместиться;
3) Масса Земли не должна измениться;
4) Поверхность не должна деформироваться.
Идеально задача регуляризации не может быть решена.
Регуляризацию можно осуществить двумя способами:
1. Построить уровенную поверхность на каком-то определенном уровне, чтобы скрыть все выступающие части (например, на высоте 10 км). Однако, способ не находит широкого применения, потому что аномалии на такой высоте сильно сглажены.
2. Удаление масс с помощью введения различных поправок. Этот способ применяется гораздо шире. Варианты введения поправок:
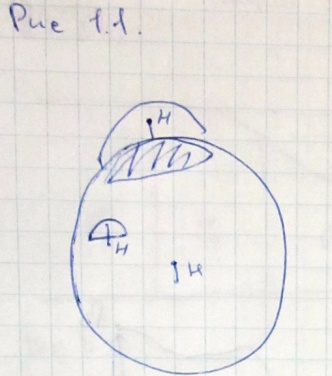
А) поправка в свободном воздухе, поправка за высоту (рис 1.1):
При введении этой поправки, выполняется только одно условие: не меняется масса, однако, искажения небольшие. И поэтому при решении геодезических задач используются аномалии в редукции Фая.
Б) поправка Буге:
- поправка за промежуточный слой. С точки
зрения регуляризации, она хуже
удовлетворяет условиям, зато для
геологических целей применяются аномалии
в редукции Буге.
В) Изостатическая редукция
δgкомпенсационная – влияние масс, перенесенных под уровень моря, это как бы компенсация дефекта масс под уровнем моря. При этом топографические массы перемещаются на большие расстояния, что приводит к большим деформациям геоида.
Г) Регуляризация методом инверсии (рис 1.2.). Это когда топографические массы перемещаются внутрь Земли, так чтобы:
Метод предложен Рудзским. Это очень трудоемкий метод, поэтому широко не используется.
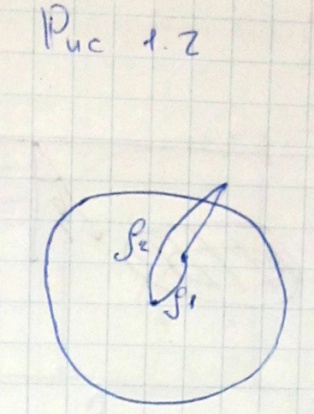
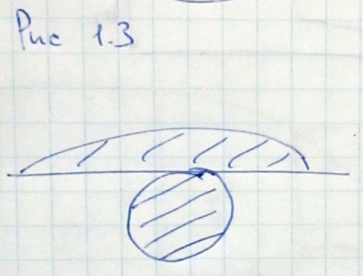
Д) Метод эквивалентной замены (рис 1.3). Когда выступающая топографическая масса заменяется эквивалентным по гравитационному действию источником, помещенного внутрь.
Где 
- нормальный градиент, а 
- аномальный градиент. Некоторые ученые
считают эту поправку наилучшей.
