Определим rб, rk, rэ, β, rk*

r_э, r_к – сопротивление базо-эмиттерного, базо-коллекторного перехода

r_б – сопротивление тела базы

r_k^*– сопротивление коллекторного перехода. r_k^*= r_к/(1+β)

α – коэффициент передачи тока. α<1

β=α/(1-α) – коэффициент усиления тока.

Сопротивление r_э определяется формулой

, где

φ_t – температурный потенциал;

Т – температура, К

Ток I_э примем ≈I_кА=0,5 [мА]

Сопротивление r_б=h₁₁ – (1+β)·r_э=413 [Ом]

Сопротивление ,

Отсюда r_k=(1+β)·r_k^*=422 [кОм].

Топологическое описание схемы.

Топология электрических схем – это способ соединения отдельных компонентов схем (конфигурации схем).

Топологическое описание схемы выполняется разными способами, например, графами. Граф – это совокупность отрезков произвольной длины и формы, называемых ветвями (ребрами) и точек пересечения ветвей – вершин.

Для составления графа воспользуемся эквивалентной схемой замещения транзистора.

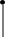
βI_б

r_б

1 2 С_к 3

С_э r_k* I(U)

U_вх r_э

4

R_H

R

5

E

Пронумеруем узлы, проставим направление токов и составляем граф.

βI_б

2 c_k 3 I(U) 4

r_б R

1 r_к* 5

r_э R_н

С_э

U_вх E

(0)

Математическая модель схемы.

Математическая модель схемы составляется по методу переменных состояния. Достоинство этого метода состоит в том, что он позволяет сформулировать ММС в виде системы дифференциальных уравнений, т.е. в форме Коши с минимальным набором переменных. Идея метода заключается в том, что базисными координатами являются те, которые фактически определяют состояния схемы, т.е. наполнение в схеме энергии.

Алгоритм составления ММС следующий:

1. Задаются исходные значения на ветвях собственного дерева U_c1(0),…,U_cn(0).

2. По уравнению U_св=-F·U_в при известной матрицы F определяются напряжения на связях являющихся зависимыми переменными.

3. Определяются токи связей с учетом полученных на этапе 2 напряжений U_св и ММК схемы.

4. Определяются токи ветвей через транспортную матрицу F по уравнению I_в=F^т·I_св

5. Токи ветвей через ММК выражаются через U_в и цикл, таким образом, замыкается.

Выделим из графа дерево.

Составим матрицу F:

По уравнению U_св=-F·U_в составляем уравнения

По известным ммк образующих связи сформулируем вектор токов Iсв.

Получаем систему уравнений:

На следующем этапе через F^T по I_в=F^т·I_св переходим к I_в:

Получаем систему уравнений:

В ММК подставляем последнюю систему уравнений, при этом подстановка токов I_вх и I_E не имеет смысла, т.к. U_вх и Е от I не зависят.

С – ветви имеют следующие ММ:

Данная система уравнений является ММС.