10.4. Общие вопросы прочности крыла

При расчете на прочность авиационных конструкций, основным видом которого является расчет на действие разрушающих нагрузок, применяется метод редукционных коэффициентов, учитывающий различие механических характеристик и условий работы отдельных элементов конструкции [6].

Различие механических свойств имеется уже в исходном, ненагруженном состоянии элементов, если они выполнены из материалов с различными значениями модуля упругости Е. Это различие механических свойств усиливается по мере роста нагрузки, когда деформация части элементов отклоняется от закона Гука за счет перехода в область пластической деформации (т. е. напряжение в материале конструкции превышает предел пропорциональности) и элементы, у которых напряжение достигло критического значения, теряют устойчивость.

Основными характеристиками механических свойств силовых элементов, используемыми при расчете, являются их диаграммы растяжения–сжатия.

Для того, чтобы при расчете на растяжение или сжатие конструкции из разнородных элементов применить обычные формулы сопромата (справедливые только в пределах действия закона Гука, т. е. до предела пропорциональности), можно все эти элементы условно заменить фиктивными элементами, имеющими единую прямолинейную диаграмму (напряжение деформации).

Обычно процесс замены осуществляется приведением к прямой закона Гука действительной диаграммы, соответствующей самому прочному и жесткому элементу конструкции панели крыла (например, в лонжеронном крыле к поясу лонжерона).

Для учета неравноценности элементов их действительные площади условно заменяются редуцированными или приведенными площадями:

,

где F_ред – редуцированная площадь сечения элемента; F – действительная площадь; – редукционный коэффициент.

Отсюда

. (10.2)

При этом ставится условие, что фиктивный и действительный элементы диаграммы (рис. 10.16) при одинаковых относительных деформациях воспринимают одинаковую нагрузку:

(10.3)

Отсюда

,

так как

,

то

.

Если фиктивный элемент имеет прямолинейную диаграмму напряжений, пропорциональную закону Гука ( ), то связь напряжений и деформаций действительного элемента и после потери устойчивости или после перехода за предел пропорциональности выражается как

.

σ

σ_ф

σ_д

ε = ε_д = ε_ф ε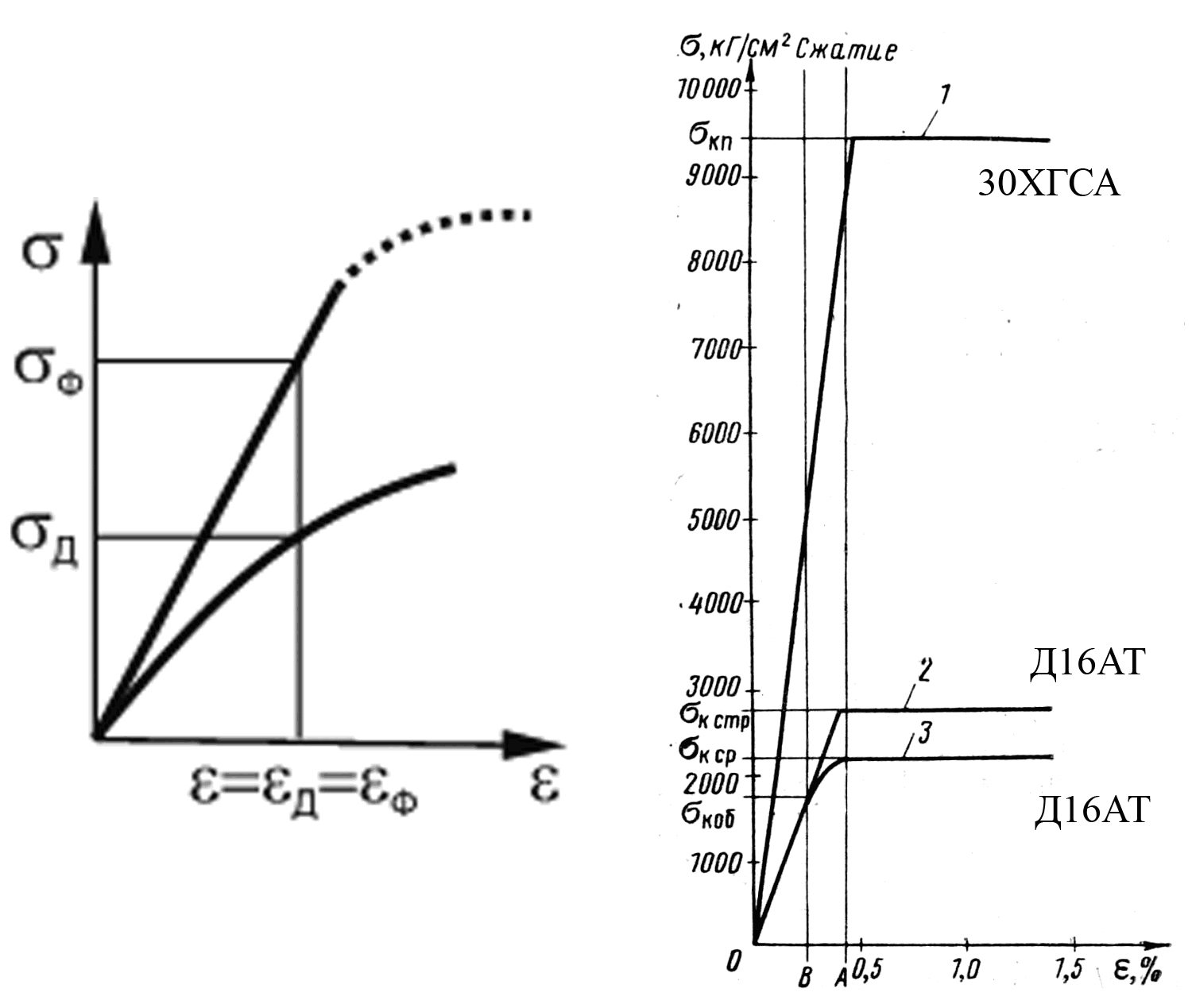

а б

Рис. 10.16. Диаграммы напряжения :

а – фиктивная; б – действительная:

1 – пояс лонжерона; 2 – стрингер; 3 – обшивка

Рассмотрим последовательность расчета методом редукционных коэффициентов для растянутой или сжатой панели крыла – статически неопределимой системы, состоящей из разнородных по своим механическим свойствам элементов, в которой действует заданное усилие Р. Элементы соединены между собой так, что продольные деформации их одинаковы (рис. 10.17).

Требуется определить напряжения в элементах системы.

Представим Р как

Так как

,

то

Тогда

и .

а

б

σ_i

σ_ф

Р

Р

Рис. 10.17. Направление в элементах панели:

а – действительной; б – редуцированной [6]

В общем случае значение находят методом последовательных приближений, так как для определения по диаграмме надо знать: или а для нахождения или _ф- редукционный коэффициент или задаваться им.

Определение проводится в следующем порядке:

1. Задается значение

2. Определяются редуцированные площади:

3. Находится фиктивное напряжение .

4. Определяются по найденному из диаграмм напряжения (см. рис. 10.16) действительные напряжения 1-го приближения

5. Вычисляются редукционные коэффициенты 1-го приближения как отношения

Расчет повторяется до тех пор, пока для каждого элемента значения не окажутся практически одинаковыми. Полученные при этом значения окончательные.

Исходные значения выбираются с учетом свойств материалов и сечений силовых элементов, силовой схемы конструкции, вида деформации и величины ожидаемых напряжений. При расчете крыла на изгиб выбор исходных значений основывается на следующих соображениях: - случаи нагружения А и являются решающими при оценке прочности для силовых элементов, обеспечивающих прочность крыла при изгибе;

- в рационально спроектированном крыле силовые элементы работают при напряжениях, близких к разрушающим;

- за разрушающие напряжения принимаются: при растяжении – предел прочности (или с учетом местного ослабления растянутых элементов); при сжатии – критическое напряжение .

Поэтому при расчете на случаи А и редукционный коэффициент принимают для каждого элемента равным отношению разрушающего напряжения элемента ( или ) к разрушающему напряжению пояса или ):

.

В других случаях нагружения М_изг значительно меньше, чем в случаях А и , поэтому принимают, что в растянутой и сжатой зонах не превышен предел пропорциональности причем в сжатой зонах т. е. и действительная, и фиктивная диаграммы линейны.

При этом по закону Гука

и

Так как

,

то

.

Такие же значения применяются во всех случаях, когда расчет ведется на действие эксплуатационных нагрузок, при которых конструкция должна работать в пределах закона Гука.

Пример действительной и схематизированной диаграммы силового элемента (дюралевого стрингера) представлен на рис. 10.18. Значение для отдельных элементов представлены в табл. 10.1 [6].