10.9. Условия прочности и характеристики прочности элементов конструкции

Общие требования прочности, установленные в нормах прочности, определяют необходимость проверки прочности конструкции при расчетных разрушающих Р^р и эксплуатационных Р^э нагрузках. Основным является, как правило, условие прочности по Р^р, в общем виде выраженное зависимостями:

, (10.6)

Соответственно, условие прочности по Р^э имеет вид

,

Для элементов авиационных тонкостенных конструкций величины разрушающих _разр и _разр и допустимых в эксплуатации _доп и _доп напряжений определяются не только механическими характеристиками материала, но также и конструктивными формами и технологией изготовления элементов [1].

Растянутые элементы. К ним относятся пояса, стрингеры, обшивка растянутой панели крыла и пр. В условии прочности (10.6) для растянутых элементов принимается

где k – коэффициент ослабления; _в – временное сопротивление материала при растяжении.

Коэффициент ослабления представляется как

k = k₁ k₂,

где k₁ – коэффициент, учитывающий уменьшение площади сечения элемента отверстиями под заклепки или болты; k₂ – коэффициент, учитывающий концентрацию напряжений. Для сечений, где можно пренебречь учетом уменьшения площади (F_раб = F), k₁ = l. В остальных случаях k₁ = F_раб / F < 1, где F_раб = (0,89–0,96)F в зависимости от диаметра заклепок, размеров и типа элемента.

Коэффициент k₂ зависит от пластичности материала, диаметра и чистоты отверстий. Для авиаконструкций из дюралюминия и стали k₂ = 0,85–0,95. Отсюда диапазон изменения коэффициента ослабления k = 0,76–0,95. В каждом конкретном случае его надо выбирать с учетом рассмотренных факторов, влияющих на его величину.

Если в сечении растянутого элемента (например в обшивке) действует еще напряжение сдвига , проверка прочности ведется по третьей теории прочности. За критерий напряженного состояния принимается Условие прочности в этом случае имеет вид:

,

где _разр = k _в

Пластины, теряющие устойчивость при сжатии и сдвиге. Это могут быть участки стенок лонжеронов, обшивки крыла и других элементов конструкций. В зависимости от того, какой вид напряжений является решающим, условие прочности имеет вид

, .

Для тонких прямоугольных пластин с большими значениями b/ критические напряжения не превышают предела пропорциональности или близкого к нему предела упругости и определяются выражениями типа формулы Эйлера, справедливыми в пределах применимости закона Гука:

(10.7)

где к – коэффициент, учитывающий условия опирания и характер внешних нагрузок, приложенных по границам пластины; b – характерный, обычно меньший, размер прямоугольника;  – толщина пластины. Для более толстых пластин, для которых формулы (10.7) дают значения _эл и _эл, превышающие пределы пропорциональности, критические напряжения можно найти по эмпирическим формулам вида:

(10.8)

где

Эмпирические формулы дают для толстых пластин критические напряжения, близкие к пределам прочности _в или _в, а для тонких пластин – близкие к Эйлеровым критическим напряжениям (рис. 10.30).

При одновременном действии на пластину напряжений сжатия и сдвига условие наступления потери устойчивости имеет вид

где _кр и _кр – критические напряжения при раздельном нагружении сжатием или сдвигом.

О

Рис. 10.30. Критические напряжения

пластины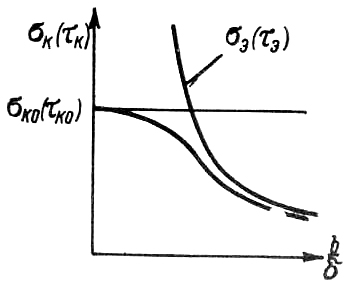

тсюда можно найти критическое нормальное напряжение с учетом действия :

и критическое касательное напряжение с учетом :

Сжатые стержни. К ним относятся пояса и стрингеры сжатой панели крыла и др.

Для сжатых стержней условие прочности выглядит как

Отверстия в сжатых стержнях, заполненные заклепками, практически не влияют на _кр. Значения _кр обычно находят по графикам _кр = f(l), где l – длина стержня, которые получены из испытаний на продольный изгиб типовых профилей.

Для длинных стержней решающей является общая потеря устойчивости – продольный изгиб оси стержня. Если сечение стержня не меняет своей формы и потеря устойчивости происходит в пределах применимости закона Гука, _кр выражается формулой Эйлера:

, (10.9)

где ; l – приведенная длина стержня, равная длине полуволны кривой, по которой происходит продольный изгиб;  учитывает опорные условия, для шарнирных опор  = 1, при упругом защемлении (имитируется при испытании приторцовкой концов стержня)  = 0,5; – радиус инерции при изгибе.

Для более коротких стержней разрушение при сжатии может начаться иногда за пределом упругости в форме как общей, так и местной потери устойчивости. В последнем случае на _кр влияет соотношение b/ для сечения стержня.

Тогда _кр находится по экспериментальным графикам, а при их отсутствии – по эмпирической формуле

(10.10)

где _кр0 – критическое напряжение местной потери устойчивости, для тонкостенных профилей оно определяется как критическое напряжение наименее устойчивого пластинчатого элемента, входящего в состав профиля, и зависит от b/ этой пластины; .