Часть 2 конструкция и прочность летательных аппаратов

Глава 9

Силы, действующие на самолет. Нормы прочности

9.1. Силы и перегрузки

Для обеспечения безопасности полетов конструкция летательных аппаратов должна быть достаточно прочной и жесткой при действии на нее нагрузок, встречающихся в эксплуатации. Необходимо, чтобы прочность и жесткость обеспечивались в течение всего срока службы летательного аппарата и были достигнуты при возможно меньшем весе его конструкции.

При оценке прочности летательного аппарата рассматриваются следующие виды эксплуатационных условий нагружения:

1) маневренный полет;

2) полет в неспокойном воздухе;

3) движение по аэродрому при взлете, посадке и рулении.

К основным нагрузкам, действующим на части летательного аппарата в этих условиях, могут добавляться:

– нагрузки от сил избыточного давления в герметических отсеках;

– нагрузки, связанные с колебаниями и большими деформациями частей конструкции (колебания, вызванные неуравновешенностью двигателя; колебания от акустических воздействий; нарастание деформаций и колебания несущих поверхностей при взаимодействии аэродинамических и упругих сил и пр.);

– силовые воздействия, возникающие при нагреве конструкции (в зоне установки двигателя, при сверхзвуковом полете).

Действие нагрузок на конструкцию проявляется и учитывается при проверке прочности по-разному в зависимости от их величины и количества повторений.

Наибольшие нагрузки, возможные в эксплуатации, но встречающиеся редко, могут вызвать остаточные деформации и даже разрушение конструкции. Они принимаются за основу при оценке необходимых для обеспечения прочности размеров конструкции и рассматриваются как приложенные однократно.

Нагрузки меньшие, но многократно встречающиеся в течение срока службы, могут привести к усталостным повреждениям конструкции. Они являются решающими при определении долговечности конструкции.

Наряду с нагрузками при оценке прочности должны учитываться факторы, которые могут повлиять на прочность, жесткость и долговечность конструкции: износ деталей, воздействие среды (разные виды коррозии), изменение свойств материалов от нагрева, радиации и т. п.

В процессе эксплуатации самолет, его агрегаты и отдельные части подвергаются воздействию разнообразных нагрузок. При этом для одних агрегатов и частей самолета наиболее опасными могут оказаться силы, действующие в полете, для других – силы, действующие при взлете и посадке. Работа агрегатов самолета под нагрузкой будет рассмотрена в следующих главах.

Нагрузки, действующие на самолет, различаются следующим образом:

– по характеру воздействия (статические – не изменяющиеся в течение длительного периода времени и динамические – быстро меняющиеся);

– по распределению (сосредоточенные, распределенные по длине, поверхности и объему конструкции);

– по величине и направлению.

Удобно все силы, действующие на самолет, разделить на две категории: силы, связанные с массой самолета и его частей (массовые силы), и силы, не связанные с массой, получившие название поверхностных сил.

Массовые силы – это сила тяжести mg и инерционные силы и определяемые нормальным и тангенциальным ускорениями. Массовые силы пропорциональны массе и распределены по всему объему конструкции.

К поверхностным силам относятся аэродинамические силы X, Y и Z, тяга двигателей Т, силы реакции земли силы взаимодействия частей самолета .

Все эти силы показаны на рис. 9.1 в скоростной системе координат ОХ_aУ_aZ_a, когда ось ОУ_a перпендикулярна вектору скорости V, a ОХ_а – параллельна V.

R_пов

y_a

y

Т

х_a

ЦМ

х

Горизонталь

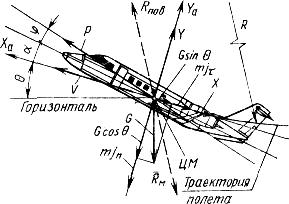
Рис. 9.1. Силы, действующие на самолет в криволинейном полете в вертикальной плоскости [1]

Заменим поверхностные силы их равнодействующей , а массовые силы – их равнодействующей Так как учтены все силы, действующие на самолет, в том числе и инерционные, то в соответствии с принципом д’Аламбера под действием этих сил самолет находится в равновесии, и равнодействующая поверхностных сил равна равнодействующей массовых сил:

(9.1)

Это справедливо для любого i-го агрегата самолета.

Оценивая нагрузки, действующие на самолет, его агрегаты и части, удобнее степень их загруженности характеризовать безразмерной величиной перегрузки n, понимая под перегрузкой отношение равнодействующей всех поверхностных сил к весу самолета G:

(9.2)

В полете , при посадке (взлете) - , где – равнодействующая аэродинамических сил X, Y, Z. Перегрузка – величина векторная, и ее направление в общем случае не совпадает с осями скоростной системы координат. Поэтому обычно пользуются проекциями перегрузки на эти оси – п_х, п_у, п_z, где

(9.3)

которые называются, соответственно, тангенциальной (продольной), нормальной и боковой перегрузками. Проекции на оси ох_а, oу_a и оz_a обозначены здесь как Пр_хR_пов, Пр_уR_пов, Пр_zR_пов; n – полная перегрузка в центре масс самолета. Выражения для определения перегрузок при движении самолета в скоростной системе координат (см. рис. 9.1) записываются в виде

(9.4)

где R – радиус кривизны траектории движения самолета (при М > 6–7 надо учитывать центробежную силу из-за кривизны Земли: mV ²/ (R₃ + H), где R₃ – радиус земного шара).

Разделив обе части в выражениях (9.4) на G, получим:

(9.5)

При малых углах α и  0 составляющие перегрузки по осям – n_x, n_у, n_z примут вид:

(9.6)

Выражения (9.5) и (9.6) позволяют определять значения перегрузок либо через известные силы, действующие на самолет, либо через параметры движения V, R и О. Перегрузка п_х определяет величину ускорения по так как п_х = (у современных маневренных самолетов максимальные значения Т / G = 1,2–1,4). Перегрузка п_х может быть и отрицательной, например, при дросселировании двигателей и выпуске тормозных щитков. Перегрузка п_у определяет маневренные возможности самолета, искривление траектории его движения j_n = V ² / R в плоскости X_aOY_a и, как будет показано ниже, в плоскости X_aOZ_a. В эксплуатации п_у может достигать значений на порядок больших, чем п_х. Перегрузка п_z определяет при отсутствии крена искривление траектории движения самолета в плоскости Y_aOZ_a и либо вообще равна нулю при Z = 0, либо при полете со скольжением больше нуля (табл. 9.1).

Таблица 9.1