Чичилин А.А.: Лабораторные работы по электротехнике

ЛАБОРАТОРНАЯ РАБОТА 8(с)

Трёхфазные цепи

Цель работы

Опытная проверка соотношений, связывающих напряжения и токи трёхфазных цепей при соединении приёмников звездой и треугольником.

Краткие теоретические сведения

Основные определения

Трехфазная цепь  это совокупность трёхфазной системы ЭДС, трёх­­фа­з­­ной нагрузки и соединительных проводов.

Трёхфазную систему ЭДС (напряжений) получают с помощью син­­х­ронного трёхфазного генератора, в обмотках которого при вращении ротора индуктируются три синусоидальные ЭДС од­ной и той же частоты, равные по амплитуде и сдвинутые по фазе относительно друг друга на угол 120:

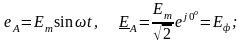
Обмотки статора генератора соединяют по схеме звезда или треугольник.

Фазы трёхфаз­ного приёмника (нагрузки) также соединяют по схеме звезда или треугольник.

В трёхфазных цепях в общем случае имеет место два вида параметров: фазное напряжение U_ф и фазный ток I_ф , а также линейное напряжение U_л и линейный ток I_л.

Для различия параметров источника и приёмника принято параметры источника указывают с прописными индексами, а параметров приёмника (нагрузки) – со строчными индексами.

Трёхфазная система ЭДС симметрична: сумма мгновенных значений ЭДС, а также комплексов ЭДС, линейных напряжений и токов соответственно равны между собой.

В зависимости от величины и характера сопротивления фаз приёмника в трёхфазных цепях нагрузка может быть симметричной: или несимметричной: . При этом несимметричная нагрузка может быть равномерной: и однородной: .

Соединение фаз приёмника звездой

Соединение фаз источника и приёмника звездой может выполняться с использованием провода, соединяющего нейтральные точки источника и при­ёмника - с нейтральным (нулевым) проводом - нейтралью (четырёхпроводная система), и без использования нулевого провода (трёхпроводная система).

При соединении звездой имеет место два вида напряжений: линейные U_AB, U_BC, U_CA и фазные U_A, U_B, U_C , а линейные токи соответствующих фаз равны фазным токам нагрузки.

Схема соединения «звезда-звезда с нейтралью» (Y₀/Y₀)

Обеспечивается независимый режим работы фаз приёмника (кроме короткого замыкания в фазе, которое недопустимо). В случае из­менения сопротивления одной фазы (в том числе при её обрыве) напряжения и токи двух других фаз не изменяются.

В этом случае напряжения на фазах приёмника (нагрузки) равны фазным нап­ряжениям источника U_a = U_A; U_b = U_B и U_c = U_C, а комплекс тока в нулевом проводе – в нейтрале, равен сумма комплексов линейных (фазных) токов I₀ = I_a + I_b + I_c.

Соблюдается следующее соотношение между линейными U_л и фазными U_ф напряжениями:

,

При симметричной нагрузке: Z_a = Z_b = Z_c, модули фазных то­­ков одинаковы и равны соответствующим линейным токам

I_ф = I_л = U_ф /Z_ф.

Расчёт токов выполняется для одной фазы.

На векторной диаграмме векторы токов составляют сим­метричную звёзду (как и векторы фазных напряжений). Следовательно, сумма ком­плексов фазных токов равна нулю

I_a + I_b + I_c = I₀ = 0

При симметричной нагрузке ток в нейтральном проводе равен нулю, и нейтральный провод можно не использовать.

При несимметричной нагрузке: Z_a Z_b Z_c, фазные токи не равны между собой и расчёт токов выполняется для каждой фазы

; ;

Следовательно, сумма ком­плексов фазных токов не равна нулю и обуславливает наличие тока в нейтральном проводе

I_a + I_b + I_c = I₀

Заключение: Для схемы «звезда-звезда с нейтральным проводом» при различных видах нагрузки напряжения на фазах нагрузки остаются постоянными.

Несимметричность нагрузки обуславливает возникновение тока в нулевом (нейтральном) проводе.

Схема соединения «звезда-звезда без нейтрали» (Y/Y)

При симметричной нагрузке: Z_a = Z_b = Z_c, условия работы цепи аналогичны условиям схемы «звезда-звезда с нулевым проводом»:

I_ф = I_л = U_ф /Z_ф.

Расчёт токов выполняется для одной фазы.

Сумма ком­плексов фазных токов равна нулю: I_a + I_b + I_c = 0

При несимметричной нагрузке: Z_a Z_b Z_c, имеет место зависимый ре­жим работы фаз приёмника: при изменении сопротивления одной фазы изменяются все фазные напряжения.

Между узлами n и N по­явится напря­же­ние смещения ней­трали

,

где Y_a = 1/Z_a; Y_b = 1/Z_b; Y_c = 1/Z_c  проводимости фаз наг­рузки.

Напряжения фаз приёмника находят из соотношений:

U_a = U_A  U_nN ; U_b = U_B  U_nN и U_c = U_C  U_nN .

В результате получается несимметричная звезда фазных напряжений приёмника - «перекос фаз». В одной из фаз, например, в фазе а, напряжение U_a может возрасти и значительно превысить фазное напряже­ние U_A генератора (что в большинстве случаев недопустимо), а в других фазах  уменьшиться.

Несимметричность фазных напряжений приёмника обусловлена разной по величине и характеру сопротивлений фаз нагруз­ки.

По этой причине в сетях с нейтральным проводом запрещается устанав­ливать предохранители и выключатели в нейтральном проводе.

Комплексы токов фаз приёмника: I_а = U_а /Z_а; I_b = U_b /Z_b; I_c = U_c /Z_c,

а их сумма равна нулю: I_a + I_b + I_c = 0.

Заключение: Для схемы «звезда-звезда без нейтрального провода» при различных видах нагрузки сумма комплексов токов фаз всегда равна нулю.

Несимметричность нагрузки обуславливает возникновение напряжения смещения нейтрали и соответствующие различие комплексов напряжений на фазах нагрузки.

Соединение фаз приёмника треугольником

При соединении фаз приёмника треугольником соотношения между параметрами трёхфазной цепи не зависят от способа соединения фаз генератора и могут рассматриваться без изображения фаз генератора.

Режим работы фаз приёмника является незави­симым (кроме короткого замыкания в фазе, которое недопустимо), так как фазные напряжения приёмника определяются линейными нап­ряже­ни­ями источника и равны им: U_ф = U_л.

Фазные токи:

I_ab = U_ab /Z_ab; I_bc = U_bc /Z_bc; I_ca = U_са /Z_ca.

Линейные токи определяют по формулам:

I_A = I_a  I_ca; I_B = I_bc  I_ab; I_C = I_ca  I_bc,

Сумма комплексов линейных токов равна нулю:

I_A + I_B + I_C = 0.

П ри симметричной нагрузке: Z_a = Z_b = Z_c, фазные токи равны между собой и их величина определяется линейным напряжением и величиной сопротивления фазы

I_ab = I_bc = I_ca = I_ф = U_л / Z_ф

На векторной диаграмме как фаз­ные, так и линейные токи образуют сим­­­­­метричные звёзды, причём

I_ab + I_bc+ I_ca = 0 и I_A + I_B + I_C = 0,

а соот­но­ше­ние между ними: I_ф = I_л / или I_л = I_ф.

При несимметричной нагрузке: Z_a Z_b Z_c, угол сдвига фаз между током и напряжением каждой фазы определяется сопротивлением нагрузки каждой фазы. Соответственно им определяются и фазные токи, а также связанные с ними и линейные токи фаз

Заключение: Для схемы подключения нагрузки, фазы которой соединены треугольником, величина фазных напряжений равна линейным напряжениям и не зависит от величины и характера нагрузки каждой фазы.

При симметричной нагрузке линейные токи фаз равны по величине.

При несимметричной нагрузке различие фазных токов обуславливает различие и линейных токов.

Мощность в трёхфазных цепях

Мощность в трёхфазных цепях синусоидального тока имеет активную и реактивную составляющие. При этом активная и реактивная мощность трёхфазной цепи определяется как сумма соответствующих мощностей каждой фазы трёхфазной цепи.

Полная мощность

При этом полная мощность в трёхфазных цепях не равна сумме полных мощностей отдельных фаз:

.

Если нагрузка симметрична, то

Соответственно:

.

При симметричной нагрузке мощность можно выразить через линейные токи и напряжения. При этом независимо от схемы соединения фаз нагрузки, используются соотношения:

;

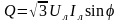При несимметричной нагрузки мощность каждой фазы рассчитывается раздельно с учётом действующих значений напряжения и тока, а также угла сдвига фаз между ними для каждой фазы цепи. При этом

Задания и методические указания к их выполнению

Задание 1: Исследовать изменение параметров трёхфазной цепи при различных условиях её работы для соединения источника и приёмника по схеме «звезда – звезда».

Работа выполняется с использованием программы моделирования и анализа электрических схем Electronics Workbench.

Модель исследуемой цепи, с компонентами для проведения необходимых измерений, приведена в файле 3ФЦ_з.ewb и на следующем рисунке:

Примечание: Измерительным приборам и переключателям в качестве обозначения приведены их функции: измеряемый параметр или выполняемое действие соответственно.

Управление переключателями выполняется нажатием цифровых клавиш, соответствующих цифре, приведённой в скобках в их обозначении.

Исходные данные

Значения параметров элементов цепи, согласно варианту, назначается следующим образом:

- величина активной составляющей сопротивления нагрузки каждой фазы – резистора R_ф:

R_ф = 50 + N, где N – номер выполняемого варианта;

- величина реактивной составляющей сопротивления нагрузки каждой фазы X_ф – используемые реактивные элементы L или C, определяется следующим образом: для нечётных вариантов реактивный элемент L и Z_ф = R + j X_L, а для чётных вариантов реактивный элемент C и Z_ф = R - j X_C.

Порядок выполнения задания

1. Открыть программу Electronics Workbench и файл исходной модели.

2. Редактировать модель цепи согласно исходным данным варианта задания.

3. Используя переключатели модели выполнить измерение параметров цепи для следующих условий её работы и зарегистрировать результаты в таблице 1 заготовки отчёта с точностью до 0,01 указанной единицы измерения параметра.

   1. При симметричной нагрузке: Z_ф = R ± j X (переключатель Za=0 разомкнут, переключатель Za=R разомкнут) для четырёхпроводного подключения нагрузки (переключатель Nn=nou замкнут).

   2. При симметричной нагрузке: Z_ф = R ± j X (переключатель Za=0 разомкнут, переключатель Za=R разомкнут) для трёхпроводного подключения нагрузки (переключатель Nn=nou разомкнут).

   3. При несимметричной нагрузке: Z_a = R (переключатель Za=0 разомкнут, переключатель Za=R замкнут), Z_b = ± j X (R_b удалено) и Z_c = R ± j X для четырёхпроводного подключения нагрузки (переключатель Nn=nou замкнут).

Внимание! Следует дождаться завершения переходных процессов (расчётов) когда величина тока фазы b будет приблизительно равен расчётному значению: I_b = U_b /Z_b

4. При несимметричной нагрузке: Z_a = R (переключатель Za=0 разомкнут, переключатель Za=R замкнут), Z_b = ± j X (R_b удалено) и Z_c = R ± j X для трёхпроводного подключения нагрузки (переключатель Nn=nou разомкнут).

1. Сохранить в рабочей папке модель исследуемой цепи в файл с именем NNN_81, где NNN - три последние цифры номера студенческого билета (зачётной книжки) исполнителя.

Задание 2: Исследовать изменение параметров трёхфазной цепи при различных условиях её работы для соединения источника и приёмника по схеме «звезда – треугольник».

Работа выполняется с использованием программы моделирования и анализа электрических схем Electronics Workbench.

Модель исследуемой цепи, с компонентами для проведения необходимых измерений, приведена в файле 3ФЦ_т.ewb и на следующем рисунке:

Примечание: Измерительным приборам и переключателям в качестве обозначения приведены их функции: измеряемый параметр или выполняемое действие соответственно.

Управление переключателями выполняется нажатием цифровых клавиш, соответствующих цифре, приведённой в скобках в их обозначении.

Исходные данные

Значения параметров элементов цепи, согласно варианту, назначается согласно исходным данным задания 1.

Порядок выполнения задания

1. Открыть программу Electronics Workbench и файл исходной модели.

2. Редактировать модель цепи согласно варианту задания.

3. Используя переключатели модели выполнить измерение параметров цепи для следующих условий её работы и зарегистрировать результаты в таблице 1 заготовки отчёта с точностью до 0,01 указанной единицы измерения параметра.

1. При симметричной нагрузке: Z_ф = R ± j X (переключатели C=nou и Zca=nou замкнуты, переключатель Zсa=R разомкнут).

2. При несимметричной нагрузке: Z_ab = R ± j X, Z_bc = ± j X (R_bc удалено) и Z_ca = R (переключатель Zсa=R замкнут, переключатели C=nou и Zca=nou замкнуты).

Внимание! Следует дождаться завершения переходных процессов (расчётов) когда величина тока фазы ас будет приблизительно равен расчётному значению:

I_ас = U_ас /Z_ас

4. Сохранить в рабочей папке модель исследуемой цепи в файл с именем NNN_82, где NNN - три последние цифры номера студенческого билета (зачётной книжки) исполнителя.

Задание 3: По результатам проведённых исследований построить с учётом масштабов векторные диаграммы токов и напряжений, действующих в фазах нагрузки.

1 . Фазные углы определить по следующей формуле:

2. Каждую векторную диаграмму предварить схемой, соответствующей режиму работы цепи с указанием элементов нагрузки каждой фазы и условий её работы.

В качестве исходных, использовать следующие изображения схем подключения:

а) при соединении нагрузки звездой	б) при соединении нагрузки треугольником

3. Для соединения нагрузки звездой определить:

- соотношения между линейными и фазными напряжениями и токами при симметричной нагрузке;

- для режима с нулевым проводом при несимметричной нагрузке сравнить с учётом масштаба величину (модуля) тока I_N , полученную по результатам его построения, с его величиной, полученной по результатам исследования;

- для режима без нулевого провода при несимметричной нагрузке сравнить с учётом масштаба величину (модуля) напряжения смещения нейтрали U_nN , полученную по результатам его построения, с его величиной, полученной по результатам исследований.

4. Для соединения нагрузки треугольником определить:

- соотношения между линейными и фазными токами и напряжениями при симметричной нагрузке;

- сравнить с учётом масштаба величину (модулей) линейных токов I_A , I_B и I_C, полученные по результатам их построений, с их величинами, полученными по результатам исследований.

5. Для каждой схемы соединения нагрузки, используя результаты измерений, определить активную, реактивную и полную потребляемую мощность, как при симметричной, так и несимметричной нагрузке.

При симметричной нагрузке расчёт потребляемых мощностей выполнить как через фазные токи и напряжения, так и через линейные токи и напряжения.