1.8 Математическое ожидание и дисперсия. Мода и медиана

Средним значением или математическим ожиданием непрерывной случайной величины Х называется значение интеграла

М(Х) = М_х = , (23)

где f(x) – плотность вероятности.

Дисперсией непрерывной случайной величины Х называется значение интеграла

D(X) = D_x= . (24)

Для определения дисперсии может быть использована формула

D_x = (25)

Модой М_о(Х) непрерывной случайной величины Х называется такое значение этой величины, плотность вероятности которого максимальна.

Медианой М_е(Х) непрерывной случайной величины Х называется такое ее значение, при котором выполняется равенство

Р(Х М_е) = Р (ХМ_е) (26)

1.9 Равномерное распределение

Непрерывное случайная величина называется равномерно распределенной на отрезке [a,b], если ее плотность вероятности имеет вид

F (x) = (27)

Математическое ожидание и дисперсия равномерно распределенной случайной величины определяются выражениями

М_х = a+b/2 (28)

D_x = (b-a)² /12 (29)

1.10 Выборка и её распределение

Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка. Объёмом совокупности (выборочной или генеральной) называется число объектов этой совокупности.

После составления выборки можно поступить 2-мя способами. После того как объект отобран и обследован он может быть возвращён или не возвращён в генеральную совокупность. Поэтому выборки подразделяются на повторные и бесповторные.

Бесповторной называют выборку при которой отборный объект не возвращается в генеральную совокупность. Повторной называют выборку при которой перед отбором следующей выборки возвращается в генеральную совокупность.

Статистические распределения выборки. Объём выборки равен:

n=n₁+n₂+…+n_k (30)

Наблюдаемые значения x_i- называются вариантами.

Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом.

Числа n₁,n₂, … ,n_k называются частотами наблюдений. А их отношение к объёму всей выборки называется относительными частотами.

(31)

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

Эмпирической функцией распределения называют функцию F^*(x), определяющую для каждого значения x относительную частоту события X<x.

F^*(x)= (32)

где n_x- число вариант,

n- объём выборки.

Свойства функции F^*(x):

1. 0≤ F^*(x)≤1

2. F^*(x) не убывающая функция.

3. Если x₁- наименьшая варианта, то F^*(x)=0 для любых X<x.

Если x_k- наибольшая варианта, то F^*(x)=1, X>x₂.

Полигоном частот называют ломанную, отрезки, которой соединяют точки (x_i;n_i). По оси абсцисс откладывают точки x_i, а по оси ординат - соответствующие значения n_i (частоты). Точки (x_i;n_i) соединяют отрезками прямых. Если вместо частот n_i брать относительные частоты, то можно построить полигон относительных частот, соединив точки (x_i;w_i) отрезками прямых.

Гистограммой называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат отрезки длиной h, а высоты равны . Величина называется плотностью частоты.

Площадь всей ступенчатой фигуры равна:

n₁+n₂+…+n_k=n (33)

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, и высотою .

w₁+w₂+…+w_n=1 (34)

Площадь всей гистограммы относительных частот равна 1.

1.11 Вариационный ряд и его числовые характеристики

Выбор объекта из генеральной совокупности и измерение значения признака называется статистическим наблюдением. Признак- это значение случайной величины. Результаты этих наблюдений фиксируются в протоколе и дневнике наблюдения в порядке их появления.

Если количество вариант слишком велико или близко к объёму выборки, то целесообразно составить вариационный ряд по интервалам значений.

По интервалам составляется также вариационные ряды для непрерывной генеральной совокупности.

Числовые характеристики вариационного ряда. Эмпирическая функция распределения.

0, x≤ x₁

F^*(x)= (35)

……………………..

1, x> x_k

Стоящие выражения в правой части будем называть накопленными частотами. Если вариационный ряд составлен по интервалам значений, то в качестве представителя интервала берут середину интервала, можно также брать и правый конец интервала.

Числовые характеристики выборки.

Среднее арифметическое определяется по формуле:

= (36)

Если вариационный ряд уже составлен, то:

= (37)

где x_k- варианты случайной величины,

n_k- соответствующие им частоты.

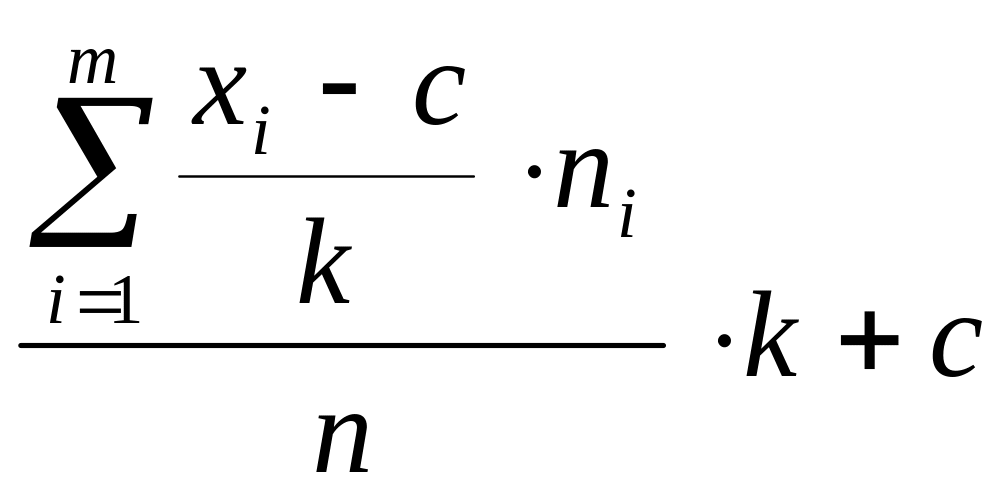= (38)

c- ложный ноль, с помощью него можно уменьшить значения чисел,

x_i- варианты,

Число k- постоянный шаг вычислений.

Если вариационный ряд составлен по интервалам, то за c следует взять середину интервала.

Формулы (37) и (38) также можно упростить следующим образом:

= (39)

= (40)

Дисперсия выборки.

Дисперсия выборки вычисляется по формуле:

(41)

(42)

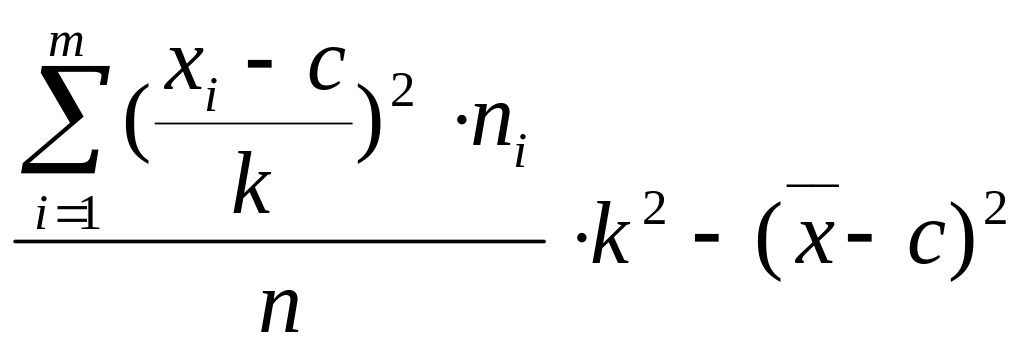= (43)

Среднее квадратичное отклонение (стандартное отклонение):

= (44) Если вариационный ряд составлен по значениям генеральной совокупности, то модой выборки называется значение, имеющее максимальную частоту.

Если вариационный ряд составлен по интервалам значений, то:

M_o=x₀+k· (45)

x₀- значение модального интервала, имеющего максимальную частоту,

k- длина модального интервала,

n_i- частота модального интервала,

n_i-1,n_i+1- частоты, соответственно предшествующего и последующего за модальным интервалом.

16