Классическое и статистическое определение вероятности

При классическом определении вероятность события определяет­ся равенством

P(A)=m/n,

где м —число элементарных исходов испытания, благоприятствующих появлению событии А; п—общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы обра­зуют полную группу и равновозможны.

Относительная частота события А определяется равенством

W(А) = т/п.

где т —число испытаний, в которых событие А наступило; n — общее число произведенных испытаний.

При статистическом определении в качестве вероятности событии принимают его относительную частоту.

Теоремы сложения и умножения вероятностей

Теорема сложения вероятностей несовместных событий. Вероят­ность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А + В) = Р(А) + Р(8).

Следствие. Вероятность появления одного из нескольких по-парно несовместных событий, безразлично какого, равна сумме веро­ятностей этих событий:

Теорем» сложения вероятностей совместных событий. Вероят­ность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Р (А+В)=Р (А) + Р (В)-Р (АВ).

Теорема может быть обобщена на любое конечное число сов­местных событий. Например, для трех совместных событии

Р(А+В + С)=Р(А) + Р(В) + + P(C) — P(AB)—P(AC)—P(BC)+P(ABC).

Теорема умножения вероятностей. Вероятность совместного по­явления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

В частности, для независимых событий Р(АВ) = Р(А)Р{В),

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности

в сех остальных, причем вероятность каждого последую­щего события вычисляют в предложении, что все предыдущие собы­тия уже наступили:

В частности, вероятность совместного появления нескольких событий независимых в совокупности, равна произведению вероятностей этих событий:

Формула полной вероятности

Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) образующих полную группу, равна сумме произведений вероятно­стей каждой из гипотез на соответствующую условную вероятность события А:

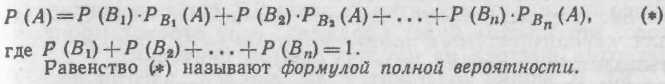
Формуле Бейеса

Пусть событие А может наступить лишь при условии появле­ ния одного из несовместных событий (гипотез) B1. В2 Вn, кото­ рые образуют полную группу событий, Если событие А уже про- изошло, то вероятности гипотез могут быть переоценены по фор­ мулам Бейеса

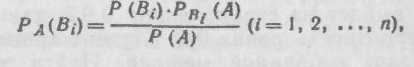
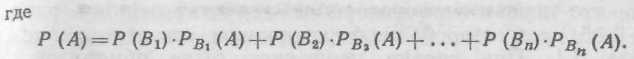
Формула Бернулли

Если производятся испытания, при которых вероятность появ­ления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относитель но события А. В § 1 — 4 этой главы рассматриваются независимые испытания, в каждом из которых вероятность появления события одинакова.

Формула Бернуллн. Вероятность того, что в п независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < I), событие наступит ровно k раз (безразлично, в какой последовательности), равна

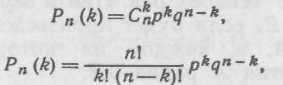
где q= 1—р.

Вероятность того, что в п испытаниях событие наступит: а) ме­нее k раз; б) более k раз; в) не менее к раз; г) не более k раз, — находят соответственно по формулам:

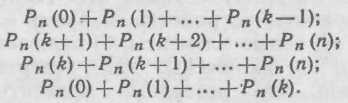
Производящая функция

В предыдущих параграфах этой главы рассматривались испыта­ния с одинаковыми вероятностями появления события; рассмот­рим испытания, в которых вероятности появления события раз­личны.

Пусть производится п независимых испытаний, причем в первом испытании вероятность появления события А равна р1, во втором— p₂, ..., в n-м испытании—р_n; вероятности непоявления события А соответственно равны q_1,q₂ ,…,q_n;Р_n(k) -- вероятность появления события А в п испытаниях ровно k раз.

Производящей функцией вероятностей Рn(к) называют функцию,

определяемую равенством

Вероятность Рn(к) того, что в n независимых испытаниях, в пер­вом из которых вероятность появления события А равна P1, во вто­ром р2 и т. Д., событие А появится ровно k раз, равна коэффициенту при zк в разложении производящей функции по степеням 2. На­пример, если n =2, то

Здесь коэффициент р1р2 при z^г равен вероятности P2 (2) того, что событие А появится ровно два раза в двух испытаниях; коэф­фициент р1q2+р2q1 ghb z1 равен вероятности Р2(1) того, что собы­тие А появится ровно один раз; коэффициент при Z0. т. е. свободный член q1q2 равен вероятности Р2 (0) того, что событие А не появится ни одного раза,

Заметим, что если в различных испытаниях появляются раз­личные события (я первом испытании событие A_lt во втором — событие А2 и т. д.), то изменяется лишь истолкование коэффициен­тов при различных степенях г. Например, в приведенном выше раз­ложении коэффициент p1P2 определяет вероятность появления двух событий A1 и А2.

Закон распределения вероятностей дискретной случайной величины. Законы биномиальный и Пуассона

Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа (т. е. между двумя соседними возможными значениями нет возможных значении), кото­рые эта величина принимает с определенными вероятностями. Дру­гими словами, возможные значения дискретной случайной величины можно перенумеровать. Число возможных значений дискретной слу­чайной величины может быть конечным или бесконечным (в послед­нем случае множество всех возможных значений называют счетным).

Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей. Закон распределения дискретной случайной величины X может быть, задан в виде таблицы, первая строка которой содержит возможные значения Хi, а вторая—вероятности р;:

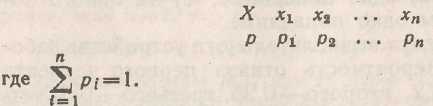
Если множество возможных значений X бесконечно (счетно), то ряд Р1 + Р2+.. сходится и его сумма равна единице.

Закон распределения дискретной случайной величины может быть также задан аналитически (в виде формулы)

или с помощью функции распределения.

Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки М₁ (х₁ p₁), M₂ (Х₂ P₂),…,М_n (х_n; р_n) (х_i—возможные значения X, р_i—соответствующие вероятности) и соединяют их от­резками прямых. Полученную фигуру называют многоугольником распределения.

Биномиальным называют закон распределения дискретной слу­чайной величины X—числа появлений события в я независимых испытаниях, в каждом из которых вероятность появления события равна р; вероятность возможного значения X — k (числа k появлений события) вычисляют по формуле Бернулли:

Если число испытаний велико, а вероятность р появления со­бытия в каждом испытании очень мала, то используют приближенную формулу

где k—число появлений события в п независимых испытаниях, Y — пр (среднее число появлений события в п испытаниях), и говорят, что случайная величина распределена по закону Пуассона.