Тема 2 Построение функции спроса на основе кардиналистского подхода к оценке полезности

Кардиналистский(количественный) подход основывается на трех положениях.

Первое: потребитель выражает свое желание приобрести какое-либо благо посредством количественной оценки его полезности. Оценки полезности являются субъективными, поскольку важнейшим принципом микроэкономики является принцип субъективизма. Полезность измеряется в ютилах. Существует общая (TU) и предельная (MU) полезности блага Х, где Зависимость между полезностью, получаемой потребителем, и количеством потребляемых им благ называется функцией полезности U = f(x).

Для моделирования поведения потребителя целесообразно ис­пользовать целевую функцию потребления. Такого рода целевая функция является частным случаем функции полезности, которая, в свою очередь, представляет математическую модель потребитель­ских предпочтений.

В экономическом анализе в качестве функций полезности часто используются линейные, квадратичные, логарифмические:

(1.13)

функции с постоянной эластичностью замещения:

(1.14)

В прикладных исследованиях спроса и потребления получила распространение линейная модель Стоуна — Джири, целевая функция которой задается в форме:

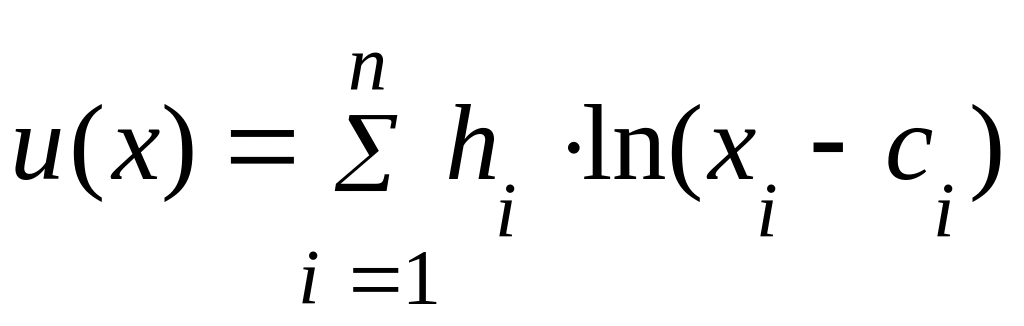(1.15)

где h_i - коэффициент, задающий приоритет потребления i-го блага;

с_i - минимальный объем его потребления.

В условиях же неопределенности анализ поведения потребителей еще более усложняется. Возникает необходимость выведения функции ожидаемой полезности, что осложняется отсутствием полной или достоверной информации о предлагаемых товарах. Так, функция ожидаемой полезности может быть представлена в следующем виде:

, (1.16)

где х – набор благ;

p – вероятность получения низкой полезности и степени удовлетворенности;

(1-p) – вероятность получения требуемой полезности и степени удовлетворения от набора благ (х).

u₁ – низкий уровень полезности;

u₂ – требуемый уровень полезности.

Потребитель стремиться максимизировать свою функцию полезности В связи с этим возникает вопрос о выведении косвенной функции полезности.

Х. Р. Вэриан отмечает, что косвенная полезность, по определению, является максимальной полезностью при ограничении:

, (1.17)

где I — доход индивида;

р, — цена на i-е благо;

х₁, ..., х_п — купленное индивидом количество благ.

Поэтому функция косвенной полезности (indirect utility function) имеет вид:

(1.18)

Второе: в соответствии с первым законом Г.Г. Госсена предельная полезность благ убывает (см. рис. 1.2).

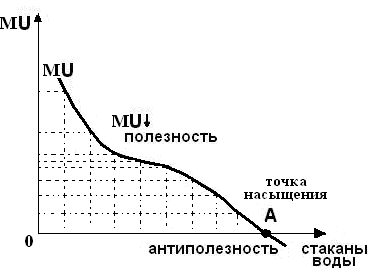
Рис. 1.2 Убывание полезности последующей единицы потребляемого блага

Поскольку предельная полезность – это первая производная функции общей полезности, то если MU = 0, общая полезность – max (min не рассматривается).

Третье: по второму закону Г.Г. Госсена оптимум или равновесие потребителя достигается в случае выполнения закона равенства взвешенных предельных полезностей:

_(1.24)

Второй закон Госсена иллюстрирует шкала Менгера (см. таблица 1).

Таблица 1 Шкала Менгера

№ блага	1	2	3	4	5	6	7	8	9	10
Общая (родовая) полезность блага (TU)	10	9	8	7	6	5	4	3	2	1
Предельная полезность, то есть полезность каждой последующей единицы блага (MU)	9	8	7	6	5	4	3	2	1
	8	7	6	5	4	3	2	1
	7	6	5	4	3	2	1
	6	5	4	3	2	1
	5	4	3	2	1
	4	3	2	1
	3	2	1
	2	1
	1

Любая диагональ с одинаковыми числами (например 4) показывает оптимальный набор благ, позволяющий получить максимальное удовлетворение от их потребления.

Шкала Менгера представляет собой дискретную функцию полезности. Если функция полезности непрерывна, то второй закон Госсена и, соответственно, функция спроса выводятся аналитически.

Народно-хозяйственная функция полезности может быть пред­ставлена в виде суммы индивидуальных функций полезности по каждому продукту, производимому в народном хозяйстве:

, (1.19)

где U - общая сумма полезности;

u_i (х_i) — функции полезности по каждому i-му продукту.

Предельная полезность будет первой производной функции по­лезности: U_i'(х_i). Она всегда будет положительной. Общим ограничи­вающим условием являются совокупные трудовые ресурсы общества:

, (1.20)

где N — ресурсы труда, приуроченные к определенному моменту времени;

а Т₁, ..., Т_п — количество труда, затрачиваемое на произ­водство каждого вида продукции.

Для определения того, какое соотношение должно быть между х₁ ..., х_n, если производство ведется целесообразно. Дело сводится к отысканию (по правилам относительных максимумов) функции Лагранжа:

(1.21)

Максимум функции достигается, если удовлетворяется усло­вие вида:

, (1.22)

которое иначе можно переписать следующим образом:

(1.23)

При рассмотрении последнего равенства можно обнаружить, что числители дробей в этой формуле есть не что иное, как предельные полезности экономических благ, а знаменатели — трудовые затра­ты на их производство. Из этой формулы следует, что предельные полезности свободно воспроизводимых экономических благ про­порциональны их трудовым стоимостям.

Контрольные задания

1. Пусть потребитель приобретает три вида блага (А, В,С), функция полезности в этом случае будет иметь следующий вид: U=f (Q_a,Q_b,Q_c). В степенном виде данная функция будет записываться следующим образом:

,

где α, β и γ– степенные коэффициенты эластичности, 0‹α‹1, 0‹β‹1 и0‹γ‹1.

Бюджетное ограничение имеет вид:

С помощью максимизации функции Лагранжа определить структуру покупок, которая обеспечит потребителю получение максимальной полезности. Вывести функции спроса на товары А, Б, С.

При неизменной структур приобретения товаров: (яблоки А, груши В, апельсины С) функция полезности имеет вид:

Доход равен 100 $,

Цена яблок (Р_А) равна 3 $ за 1 кг,

Цена груш (Р_А) равна 5 $ за 1 кг,

Цена апельсин (Р_А) равна 4 $ за 1 кг.

Рассчитать структуру покупок.

2. Пусть потребитель приобретает три вида блага (А, В и С), функция полезности будет иметь следующий вид:

,

где α, β и γ– степенные коэффициенты эластичности, 0‹α‹1, 0‹β‹1 и0‹γ‹1.

Бюджетное ограничение имеет вид:

С помощью максимизации функции Лагранжа определить структуру покупок, которая обеспечит потребителю получение максимальной полезности. Вывести функции спроса на товары А, Б, С.

2,3,1, - минимальные объемы потребления каждого блага независимо от их цен.

Доход равен 120 $,

Цена огурцов (Р_А) равна 3$ за 1 кг,

Цена картошки (Р_В) равна 1 $ за 1 кг,

Цена мяса (Р_С) равна 10 $ за 1 кг.

Рассчитать структуру покупок.