Структурные (описательные) средние.
К этим средним относятся мода и медиана. Модой называется наиболее часто встречающееся значение признака в рассматриваемой совокупности. Мода используется при экспертных оценках и различных видах статистических исследований.
Пример. Имеются данные, расположенные в порядке возрастания, о средней месячной заработной плате рабочих бригады:
16120, 16120, 16120, 16140, 16185,16215,16250.
Мода-
Медианой называется
значение признака, находящегося в центре
ранжированного ряда и делящего этот
ряд на две равные части по численности,
входящих в него единиц совокупности.
Для определения места медианы в
ранжированном ряду, вычисляется ее
номер по формуле:
.
Медиана (средний элемент) не зависит от величины всех элементов ряда, как средняя величина. Поэтому, в ряде случаев, она является более информативным показателем, чем средняя. Это особенно проявляется в ряду распределения, содержащего небольшое число элементов, существенно отличающихся от общей массы наблюдений.
На основе вышеприведенного примера, рассмотрим расчет медианы.
,
следовательно, Ме=16140руб.
Рассчитаем для
данного ряда среднюю:
Следовательно, 4/7=0,57 (57%) имеют заработную плату ниже средней.
При четном числе членов ряда, например:
16120, 16120, 16120, 16140, 16185, 16215 Также первоначально определяется номер медианы , а затем и сама медиана
Свойство медианы: сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
или
,
т.е. сумма отклонений индивидуальных
значений признака от медианы. Есть
величина минимальная.
Расчет медианы в ряду распределения.
Пример. Имеются данные о распределении группы студентов по росту. Определить среднюю, моду и медиану.
-
Рост, см.- х
Число студентов,f
Накопленные частоты,S
160
2
320
2
162
3
486
5
170
8
1360
13
180
6
1080
19
190
2
380
21
Итого
21
3626
-
Мо= 170см.
Для нахождения медианы в ряду распределения, кроме номера медианы, необходимо рассчитать накопленные частоты. Накопленными частотами называются последовательно просуммированные частоты.
Порядок действий:
Определяем
По номеру медианы и накопленным частотам находим медианное значение роста спортсмена. Для нашего примера Ме= 170см. В ранжированном ряду он был бы 11-м ,
т. е .справа и слева от него находилось бы по 10 человек
Расчет моды и медианы в интервальном ряду распределения
Модальное значение признака (Мо) рассчитывается по формуле:
,
где
-нижняя граница модального интервала;
i
- шаг интервала;
-частота
модального интервала;
-частота
интервала, предшествующего
модальному;
-частота
интервала, следующего за модальным.
Для ряда с неравными интервалами, расчет моды производится
по
следующей формуле:
,
где m - плотность распределения в соответствующем интервале.
Плотность распределения, это число случаев, приходящихся на единицу интервала.
m= f/i (абсолютная плотность распределения);
m
=
(относительная плотность распределения).
I
Расчет медианы производится по формуле:
,
где
- номер медианы;
- нижняя граница медианного интервала;
i-шаг
интервала;
- частота медианного интервала.
-
накопленные
частоты, предшествующие
медианному интервалу;
Пример. Рассчитать моду и медиану, по ниже представленным данным, о размере платежей за жилищно- коммунальные услуги (в руб.) в расчете на 1чел.(18кв. м.) по 55районам одного из регионов РФ :
Размер платежей, руб. Х. |
Число районов, f |
Накопленные частоты, S |
|
|
155-160 |
3 |
3 |
157,5 |
472,5 |
160-165 |
10 |
13 |
162,5 |
1625,0 |
165-170 |
20 |
33 |
167,5 |
3350,0 |
170-175 |
22 |
55 |
172,5 |
3795,0 |
Итого |
55 |
|
|
9242,5 |
;
;
Рассчитаем моду для ряда с неравными интервалами, используя: а) абсолютную плотность распределения; б) относительную плотность распределения.
Пример. Ниже представлено распределение вкладчиков по размерам вклада в одном из сбербанков района:
-
Размер вклада, руб.- х
Число вкладчиков,f
Частость,
Абсолютная плотность распределения,
Относительная плотность распределения,
500-1500
700
1500-5000
400
5000-7500
250
Свыше- 7500
100
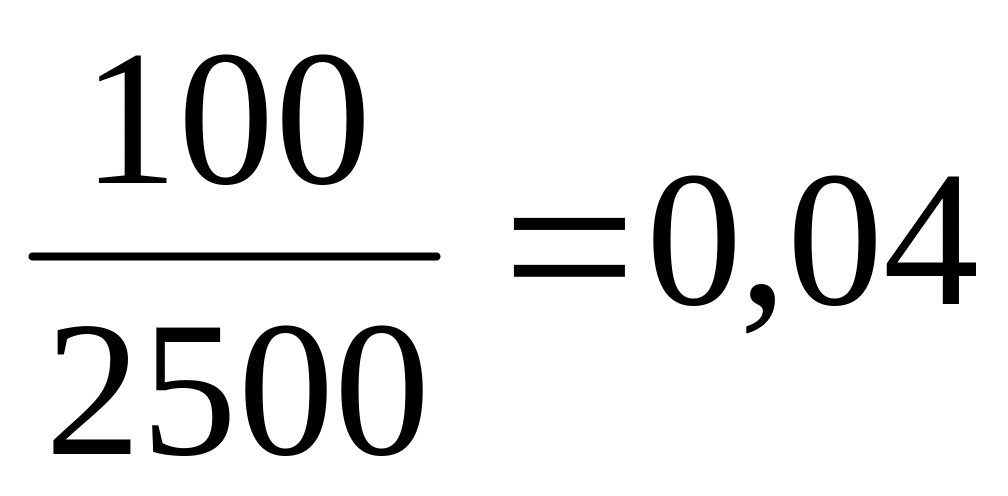
Итого
1450
1,0
а)
=
=
;
б)
Расхождение в результатах объясняется округлениями, допущенными в ходе расчетов в варианте «б».