Пользуясь формулой закона Ома, можно записать

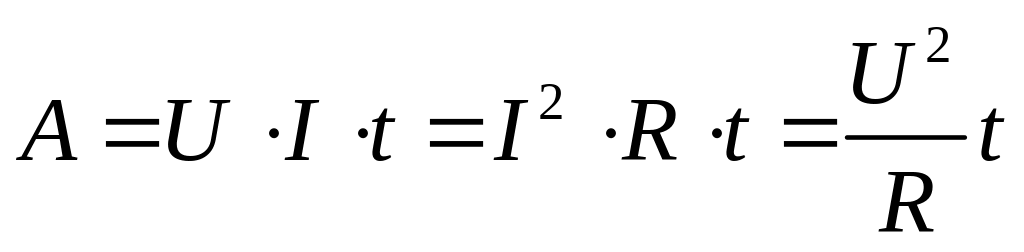
Как известно, мощность это работа в единицу времени

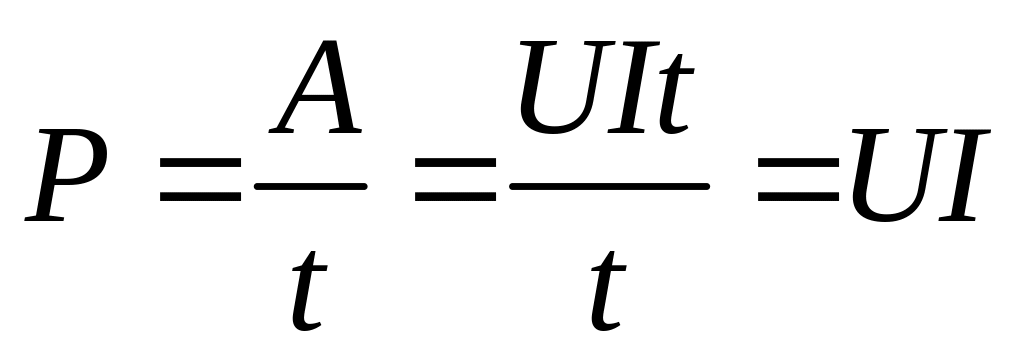, применяя закон Ома, можно также записать

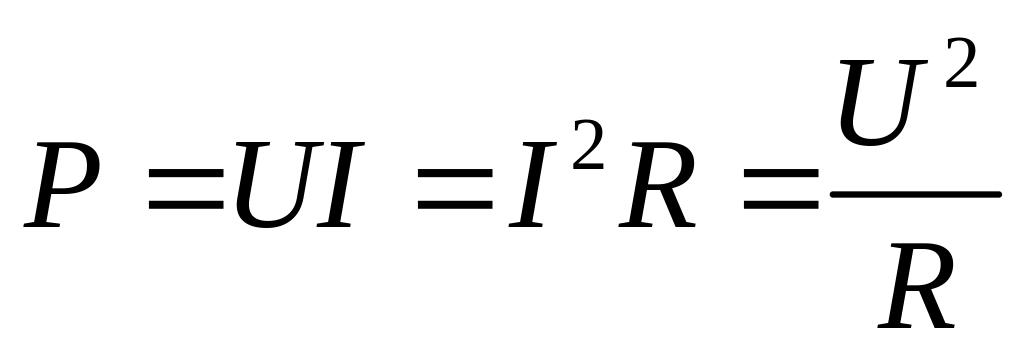
Единицы измерения мощности в радиотехнике ватт, милливатт, микроватт.

1Вт = 10³мВт = 10⁶ = мкВт; 1мВт = 10^-3 Вт = 10³ мкВт;

Один ватт это мощность, при которой в одну секунду совершается работа в один джоуль.

В энергетике применяют киловатт и мегаватт: 1кВт = 10³ Вт; 1мгВт = 10⁶ Вт;

В электрической цепи различают полную мощность, полезную мощность и мощность потерь;

Р₁=Р₂+Р₀, где Р₁- полная мощность, т.е. вся мощность развиваемая источником,

Р2- полезная мощность, это мощность отдаваемая источником во внешнюю цепь,

т.е. мощность, за счёт которой совершается полезная работа.

Р₀- мощность потерь, эта мощность обусловлена потерями внутри источника, например его нагревом.

Полную мощность можно определить также по формуле Р₁ = Е·I; Где Е – ЭДС, I- ток.

Полезная мощность Р₂ = U·I = I²·R = ; Где U-напряжение; R- сопротивление

Мощность потерь Р₀=U₀·I = I²· r; r – внутреннее сопротивление источника.

Коэффициент полезного действия электрической цепи определяют по формуле

;

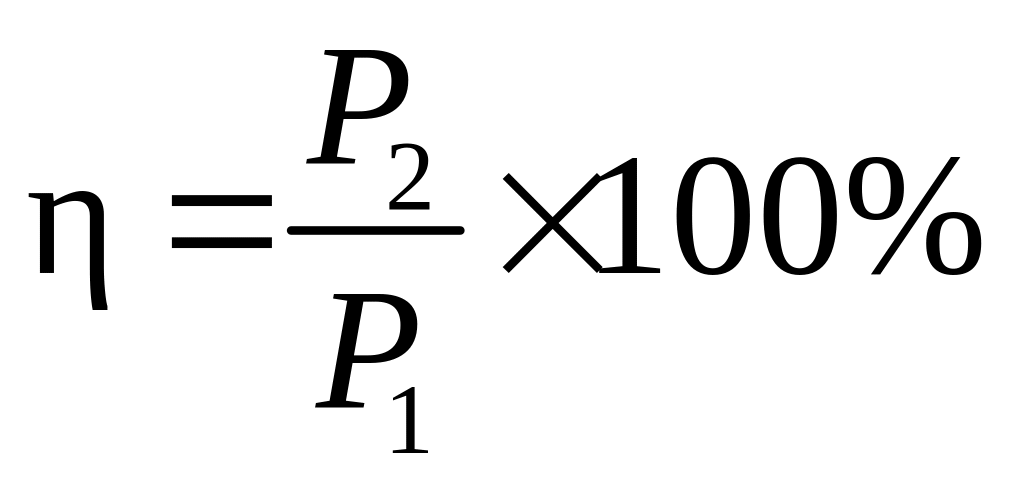Если учесть зависимость полной мощности P₁и полезной мощности P₂ от напряжения, ЭДС и тока, то величину КПД можно выразить через значения ЭДС и напряжения:

;

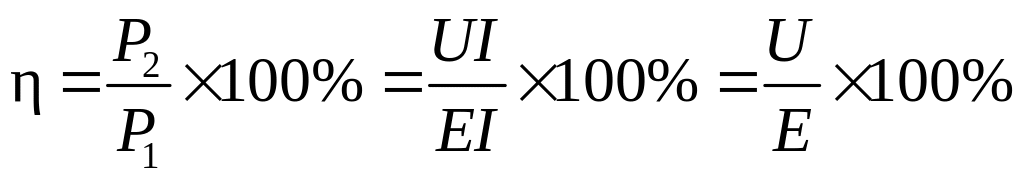Тепловое действие тока

Из всех преобразований электроэнергии в другие виды энергии, наиболее часто

электрическая энергия преобразуется в тепловую энергию, т.е. в тепло, при этом количество тепла, выделяемое в проводнике, определяется законом Джоуля-Ленца:

Q = I²·R·t, где, Q- количество теплоты в Джоулях, I-ток в Амперах, t-время в секундах.

В теплотехнических расчётах тепло измеряют в калориях, в этом случае необходимо вводить коэффициент 0,24; формула принимает вид: Q =0,24 I²·R·t;

Последовательное соединение резисторов

Это такое соединение, при котором по всем элементам схемы, в частности резисторам, протекает один и тот же ток. Рассмотрим схему, состоящую из источника и трёх сопротивлений, включенных последовательно:

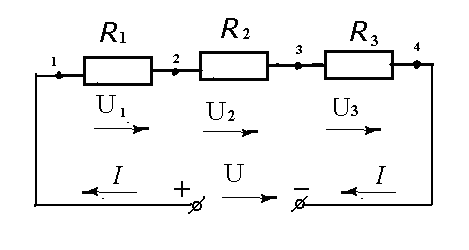
На схеме обозначено:

U- напряжение на зажимах источника; нам уже известно, что это напряжение или эта разность потенциалов возникает в источнике из-за действия сторонних сил, которые принудительно разделяют заряды и создают положительный (+) и отрицательный (–) полюсы (зажимы) источника. Величина этого напряжения меньше величины ЭДС источника на величину падения напряжения на внутреннем сопротивлении источника.

I – ток, всегда направлен от + к – на участке внешней цепи, т.е. в нагрузке (в данном случае сопротивления R₁, R₂,R₃, и в соединительных проводниках, причём в большинстве расчётов сопротивлениями проводников пренебрегают, т.е. считают их = 0. Там где сопротивлениями проводников пренебречь нельзя, там это обстоятельство оговаривают особо.

U₁, U₂, U₃ –падения напряжения на сопротивлениях R₁, R₂,R₃, которые возникают от прохождения тока по этим сопротивлениям.

С помощью вольтметра легко установить, что U= U₁+U₂+U₃ или I·Rэкв =IR₁ + IR₂+ IR₃, где Rэкв – это такое одно эквивалентное сопротивление, которое будучи включено в цепь вместо R₁, R₂,R₃ не изменит силу тока I, т.е. не изменяет режима работы цепи, далее сокращаем на величину тока I, получим

Rэкв = R₁ + R₂+ R₃

Вывод: Эквивалентное сопротивление нескольких последовательно включённых сопротивлений.

Если имеем n-одинаковых сопротивлений R, то Rэкв = n· R;

При последовательном соединении сопротивлений мощности и напряжения распределятся прямо пропорционально сопротивлениям U₁/ U_{2 =} Р₁/Р₂ = R₁/ R_2, это вытекает из того, что при одинаковом токе падение напряжения и мощность прямо пропорциональны величине сопротивления.

Пример.

Даны две лампы накаливания (обычные лампочки для освещения в квартирах) , их мощности Р₁ = 40 Вт (первая лампа), Р₂ = 100 Вт (вторая лампа). Каждая лампа имеет номинальное напряжение - 127 В. ( Номинальное – указанное заводом изготовителем, т.е. такое напряжение, на которое эти лампы рассчитаны). Можно ли эти лампы включить последовательно к источнику 220 В?

Решение: Воспользуемся формулой для мощности P= U² / R откуда, сопротивление нити накала 1-ой лампы: R₁ = U² / P₁ =127² / 40 = 403,2 Ом ;

сопротивление нити накала 2-ой лампы: R₂ = U² / P₂ =127² / 100 = 161,29 Ом;

Определяем ток в цепи: I = U / R₁ + R₂ = 220 / 403,2 + 161,29 = 0,39 А.

Найдём напряжение на каждой лампе

U₁ = I · R₁ = 0,39 · 403,2 = 157 В, U₂ = I · R₂ = 0,39 · 161,29 = 63 В.

Вывод: напряжение на первой лампе превышает допустимое, лампа будет гореть ярче обычного и поэтому она быстро перегорит, вторая лампа будет работать с недокалом, т.е. слабо. Следовательно такие лампы включать последовательно на напряжение 220 В нельзя.

Параллельное соединение резисторов. Первый закон Кирхгофа.

Это такое соединение, при котором на зажимах всех элементов имеется одно и то же напряжение. При рассмотрении схем в них можно выделить узлы и ветви. Узлом называется точка цепи, к которой подходят не менее трёх проводников.

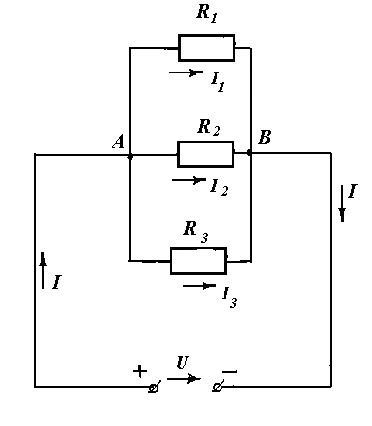
Ветвью называется часть цепи, заключённая между двумя узлами. При этом всегда в узле должна стоять точка, а в пределах ветви не может быть каких-либо ответвлений, поэтому в пределах ветви протекает один и тот же ток. На схеме мы имеем два узла: А и В, и три ветви: ветвь №1: т.А - сопротивление R₁ -т.В;

ветвь №2: т.А- сопротивление R₂- т.В;

ветвь №3: т.А- сопротивление R₃ - т.В;

Поскольку токи в узле измениться не могут, поэтому в электрических цепях всегда выполняется первый закон Кирхгофа:

сумма токов втекающих в узел равна сумме токов вытекающих из узла.

Так в узел А втекает один ток – I, вытекают три тока – I₁, I₂, I₃, следовательно, первый закон Кирхгофа для узла А: I = I₁+ I₂ + I₃, аналогично для узла В:

I₁+ I₂ + I₃ = I, втекающие токи находятся в левой части уравнения, вытекающие - в правой.

Другая формулировка 1-го закона Кирхгофа гласит: алгебраическая сумма токов в узле всегда равна нулю , чтобы записать закон в таком виде перенесём правую часть уравнения в левую, получим для узла А: I– I₁– I₂ – I₃ = 0, для узла В: I₁+ I₂ + I₃ – I = 0, т.о. втекающие токи всегда берутся со знаком +, вытекающие - со знаком –;