Энергия магнитного поля
Выше было установлено, что магнитное поле, втягивая катушку с током, совершает работу равную изменению потокосцепления, умноженному на ток, т.е. А = ∆ψ ∙ I, но если поле совершило работу, значит, оно обладало энергией равной этой работе, т.о.
W = А = ∆ψ ∙ I, где W – энергия магнитного поля. Данная формула справедлива и для уединённого контура с собственным потокосцеплением. Для такого случая это равенство будет справедливо только для бесконечно малых величин dW = dA = dψ ∙ i, где i мгновенное значение тока, т.е. это ток соответствующий значению dψ. Это вытекает из того что ток изменяясь, например при включении, изменяет и потокосцепление. Если индуктивность контура постоянна, то зависимость между потокосцеплением и током изображается в виде прямой линии.
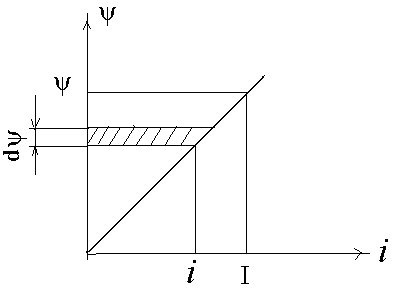
Изменение энергии dW = dψ ∙ i выразится заштрихованным элементом площади, а энергия поля при токе I и потокосцеплении ψ выразится площадью прямоугольного треугольника с основанием ψ и высотой I. Это вытекает из того что площадь треугольника равна сумме элементарных площадей, заштриховнных в этом треугольнике. Следовательно, энергия магнитного поля определится из формулы
Энергию магнитного поля контура можно выразить через его индуктивность,
т.к. L = ψ/I то
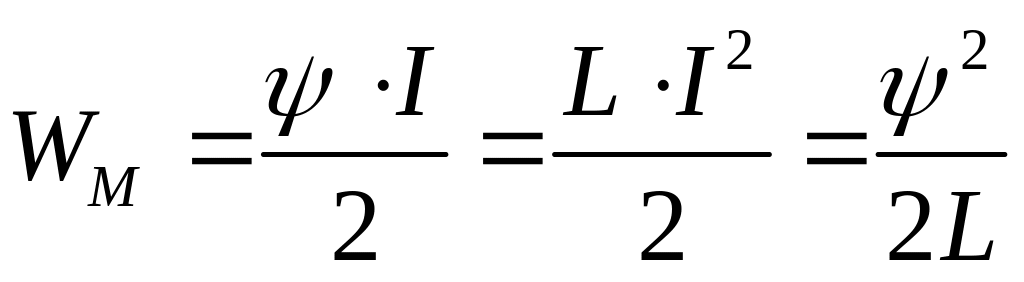
Иногда в некоторых расчётах применяют не всю энергию поля, а энергию, находящуюся в единице объёма магнитного поля. Можно доказать, что в этом случае такую энергию можно выразить через индукцию и напряжённость магнитного поля.
Энергия магнитного поля в единице объёма
.
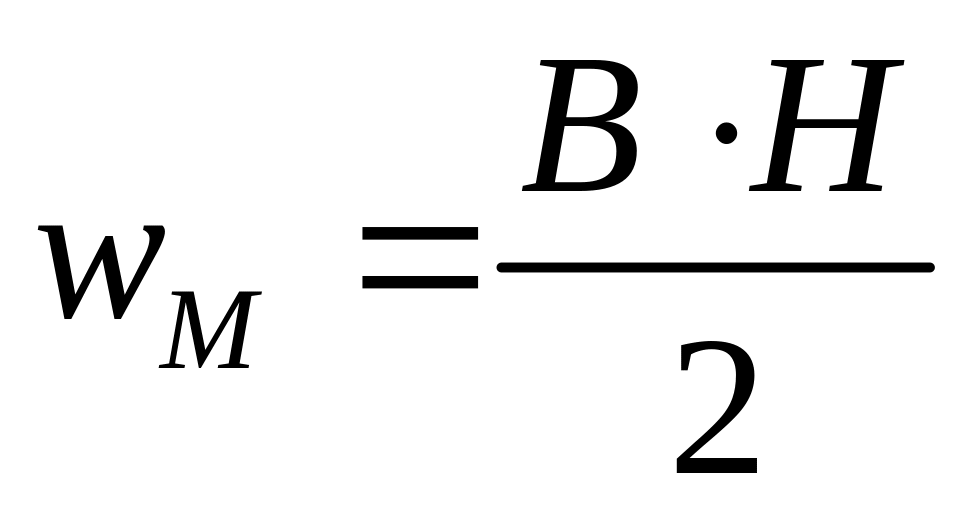Индуктивность кольцевой катушки
Ранее мы установили, что если по катушке пропускать ток, то этот ток создаст в сердечнике магнитный поток, величина которого пропорциональна току, соответственно потокосцепление также будет пропорционально току.
. Мы также знаем, что для характеристики контура или катушки в отношении образования собственного потокосцепления служит параметр, который называется индуктивность. (L)
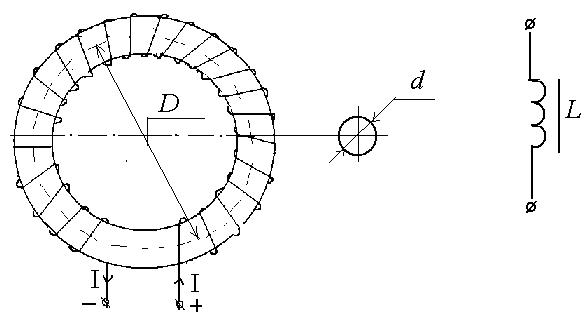
На
рис.показана индуктивность с кольцевым
сердечником, D
– диаметр по которому высчитывают длину
средней линии сердечника -
(
= πD) ,
d-
диаметр по которому высчитывают площадь
поперечного сечения сердечника – S.
(S= πD2/4)/
Справа показано условное изображение индуктивности в схемах. Вертикальная линия рядом с витками обозначает наличие сердечника.
Из закона Ома для магнитной цепи известно, что магнитный поток Ф, созданный током I, в сердечнике катушки с числом витков W будет равен
Потокосцепление
катушки
;
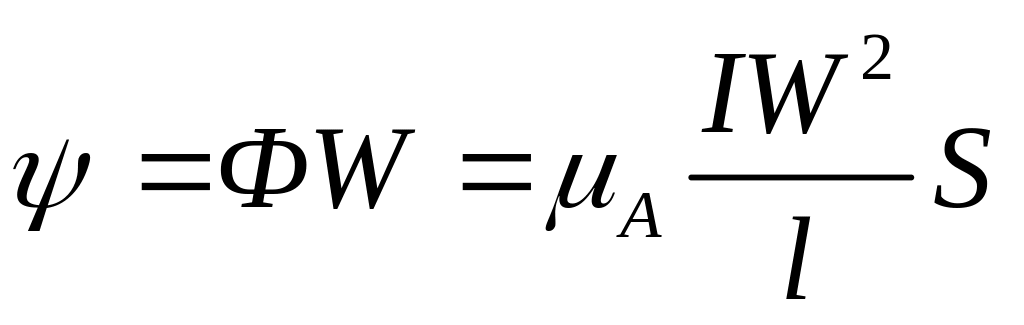В этом случае индуктивность
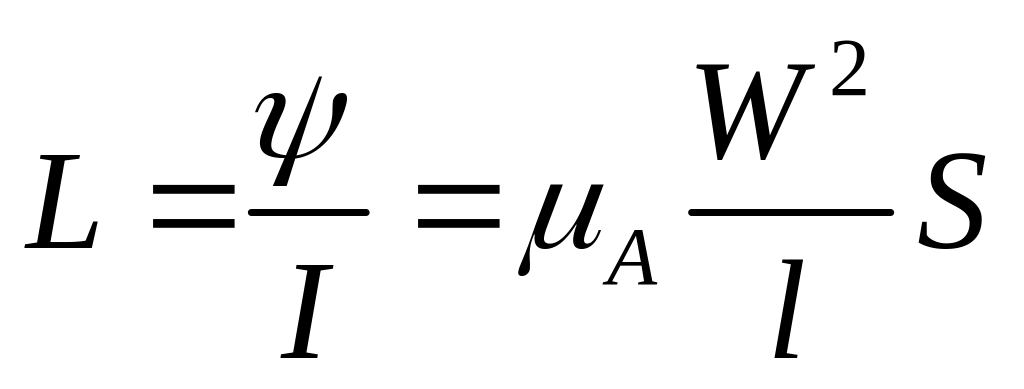
Индуктивность катушки пропорциональна квадрату числа витков и зависит от материала и габаритов катушки.
Эдс самоиндукции
Если по виткам катушки пропустить не постоянный ток, а ток, изменяющийся по величине и направлению или ток прерывистый, то он создаст в сердечнике примерно такой же по форме магнитный поток. Этот поток, пересекая витки наведёт в них ЭДС. . Такое явление называется явлением самоиндукции, а сама ЭДС называется ЭДС самоиндукции, которая является частным случаем ЭДС электромагнитной индукции. Обозначается еℓ, как мы знаем малыми буквами обозначают изменяющиеся величины.