Расчёт сложной цепи методом наложения

Метод основан на принципе независимости действия ЭДС различных источников и применим только к линейным цепям, (в этих цепях напряжение и ток связаны законом Ома). Смысл расчёта состоит в том, что мы по очереди исключаем источники, оставляя в схеме их внутренние сопротивления, и ведём расчёт как в случае простой цепи с одним источником, при этом мы находим т.н. частичные токи, напряжения и сопротивления, обозначаемые штрихами. Затем частичные токи складывают в ветвях с учётом их знаков и т.о. находят истинные токи.

Пример: Решить предыдущую задачу методом наложения.

1. Исключаем из цепи источник Е_2, оставляя его внутреннее сопротивление, получим схему

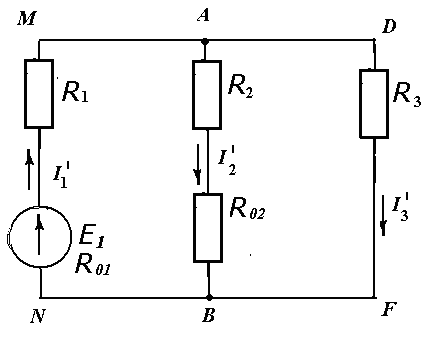
На схеме указаны частичные токи, один штрих рядом с током указывает на то что это токи от первого источника, направление этих токов выбрать легко исходя из полярности источника Е₁.

2. Находим эквивалентное сопротивление для данной схемы, при этом учитываем, что сопротивление в ветви с источником всегда включено последовательно к остальной цепи, а две другие ветви включены между собой параллельно.

Сначала для этого находим эквивалентное сопротивление двух параллельных ветвей АВ и DF

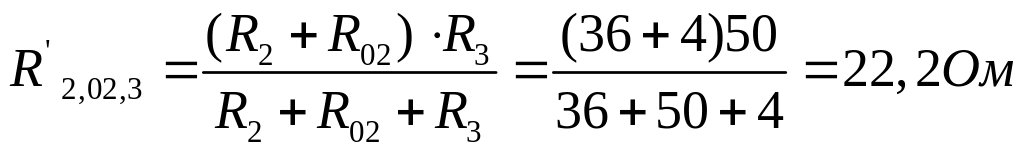
3. Находим частичный ток в ветви NM

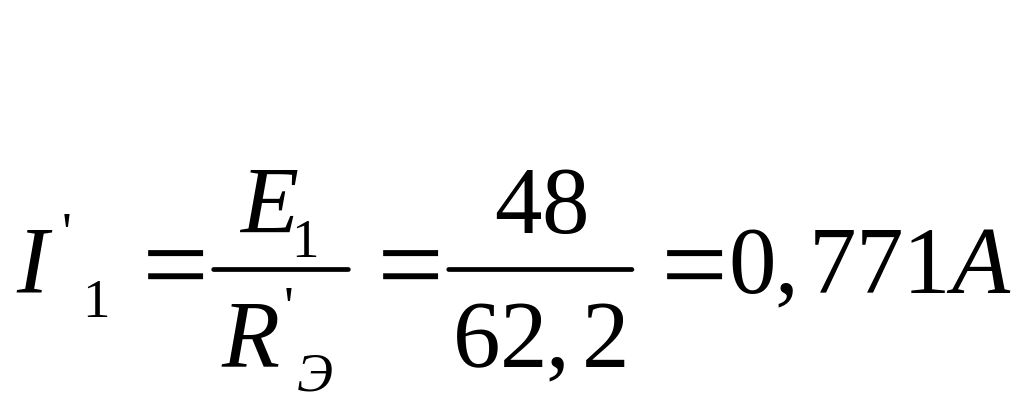
4. Находим частичное падение напряжения в ветвях при прохождении частичного тока

U’_AB = U_DF = I’₁ •R’_2,3 = 0,771 • 22,2 = 17,12 B.

5. Находим частичные токи в параллельных ветвях АВ и DF

I'₂ = U'_AB : (R ₂ + R₀₂) = 17,12 / 40 = 0,439 А.

I'₃ = U'_DF : R ₃ = 17,12 : 50 = 0,342 А.

6. Исключаем из цепи источник Е₁, оставляем источник Е₂. Цепь примет вид

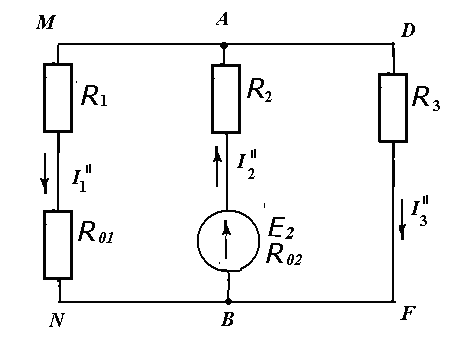
При анализе этой цепи надо снова помнить, что ветвь с источником ( АВ) включена всегда последовательно относительно остальной цепи, поэтому в нашем случае ветви MN иDF включены между собой параллельно. Чтобы это было более наглядно можно ветви MN иАВ поменять местами.

Весь остальной расчёт частичных токов с двумя штрихами аналогичен, рассмотренному выше:

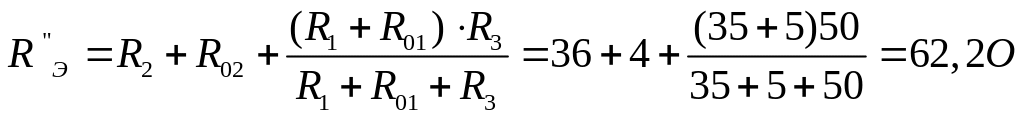
I”₂ = Е₂ / R”_Э = 36 : 62,2 = 0,579 А.

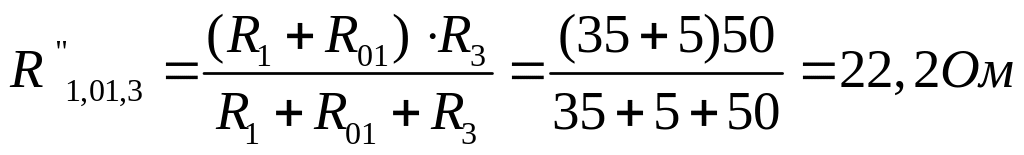
U”_MN = U”_DF = I”₂ • R”_1,01,3 = 0,579 • 22,2 = 12,83 B.

I»₁ = U»_MN / (R ₁ + R₀₁) = 12,83 / 40 = 0,321 А.

I»₃ = U»_DF / R₃ = 12,83 / 50 = 0,258 А.

7. Находим истинные токи, для чего производим наложение частичных токов (откуда название метода), т.е. складываем их алгебраически с учётом направлений.

I₁ = I’₁ – I”₁ = 0,771 – 0,321 = 0,45 А.

I₂ = I»₂ – I'₂ = 0,579 – 0,429 = 0,15 А. (от большего тока вычитаем меньший).

I₃ = I'₃ + I»₃ = 0,342 + 0,258 = 0,6 А.

Указываем на проводниках истинное направление токов, это направление совпадает с направлением большего по абсолютной величине частичного тока.

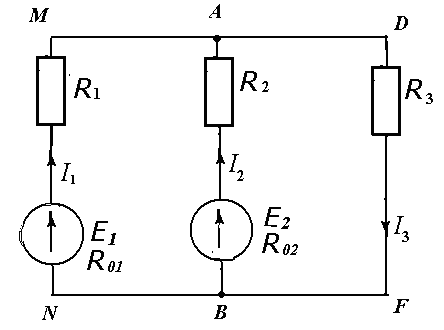
Проверка решения сделана выше.

Расчёт сложной цепи методом узловых напряжений

Узловым напряжением называется напряжение между двумя узловыми точками.

Для приведенной схемы узловое напряжение U это U = U_АВ.= U_MN = U_DF

Выведем формулу для вычисления величины U.

Из составления потенциальной диаграммы цепи известно, что применительно к нашей схеме

U = Е₁ – I₁(R₀₁ + R₁), откуда I₁ = (Е₁ – U) : (R₀₁ + R₁), = (Е₁ – U) • G₁,

где G₁ = 1 / (R₀₁ + R₁) – проводимость первой ветви

Для второй ветви аналогично

U = Е₂ – I₂•(R₀₂ + R₂), откуда I₂ = (Е₂ – U) : (R₀₂ + R₂), = (Е₂ – U) • G₂,

где G₂ = 1 / (R₀₂ + R₂) – проводимость второй ветви.

Ток в третьей ветви определится из закона Ома:

I₃ = U : R₃ = U • G₃, где G₃ = 1/ R₃ – проводимость третьей ветви.

Применим 1-ый закон Кирхгофа для узла А:

I₁+ I₂ – I₃ = 0;

(Е₁ – U) • G₁ + (Е₂ – U) • G₂ – U • G₃ = 0,

Раскрываем скобки и вычисляем узловое напряжение

Узловое напряжение равно отношению алгебраической суммы произведений ЭДС на проводимости соответствующих ветвей к сумме проводимостей всех ветвей.

Можно также показать, что если направление какой-либо ЭДС было бы противоположным, то в числителе перед этой ЭДС должен стоять знак «–».

Пример.

Дано:

Схема 1. Е₁ = 48 В, Е₂ =36 В, R₁ = 35 Ом, R₂ = 36 Ом, R₃ = 50 Ом, R₀₁ = 5 Ом, R₀₂ = 4 Ом.

Определить все токи методом узловых напряжений.

Решение:

1. Определяем проводимости ветвей

G₁ = 1/ (R₀₁ + R₁₎ = 1/ 35+5 = 0,025 См.

G₂ = 1/ (R₀₂ + R₂₎ = 1/ 36+4 = 0,025 См.

G₃ = 1/ R₃ = 1/ 50 = 0,02 См.

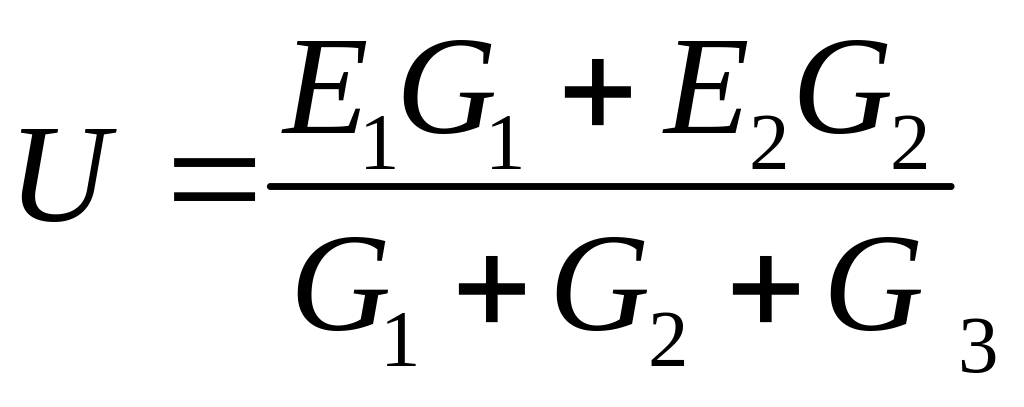= (48•0,025+36•0,025) : (0,025 +0,025 +0,02) = 30 В.

Находим токи в ветвях

I₁ = (Е₁ – U) • G₁ = (48 – 30) • 0,025 = 0,45 А.

I₂ = (Е₂ – U) • G₂ = (36 – 30) • 0,025 = 0,15 А.

I₃ = U • G₃ = 30 • 0,02 = 0,6 А.

Проверка.

Сделана выше.