Постулаты специальной теории относительности.
Преобразования Галилея и следствия из него настолько очевидны, то кажется, что они должны быть справедливыми во всех случаях. Однако в конце 19 века был обнаружен один факт, противоречащий классическому закону сложения скоростей, следовательно, и преобразованиям Галилея это постоянство скорости света в вакууме в различных инерциальных системах отсчёта. Например, скорость света при движении Земли по её орбите навстречу Солнцу и от него получалась одинаковой и равной c 3108 м/с, а не c ± , где — орбитальная скорость Земли, как это должно следовать из классического закона сложения скоростей. В связи с этим возникла необходимость в отказе от привычных представлений о пространстве и времени, используемых в классической механике, поскольку они противоречили опытному факту постоянства скорости света.
Релятивистская механика, созданная Эйнштейном, основывается на двух постулатах:
а) Принцип относительности. Все инерциальные системы отсчёта равноправны, во всех таких системах не только механические, но и все другие явления природы протекают одинаково.
б) Принцип постоянства скорости света. Во всех инерциальных системах отсчёта скорость света в вакууме одинакова и равна с.
Правильность этих постулатов и всей релятивистской механики следует из того, что следствия, получаемые из теории Эйнштейна, находят надёжное экспериментальное подтверждение. Первый постулат требует существования преобразований, аналогичных преобразованиям Галилея, которые бы оставляли неизменными уравнения механики и электродинамики при переходе от одной инерциальной системы отсчёта к другой.
Преобразования лоренца
Пусть относительно инерциальной системы отсчёта K движется со скоростью другая система отсчёта K. Для упрощения рассуждений предположим, что направления координатных осей Ox и Ox совпадают (рис. 1 предыдущей лекции). Обозначим координаты точки M в системе отсчёта K в произвольный момент времени t через x, y, z, а координаты той же точки в системе отсчёта K — через x, y, z в момент времени t. Тогда преобрaзования при переходе из системы отсчёта K в систему K имеют вид:
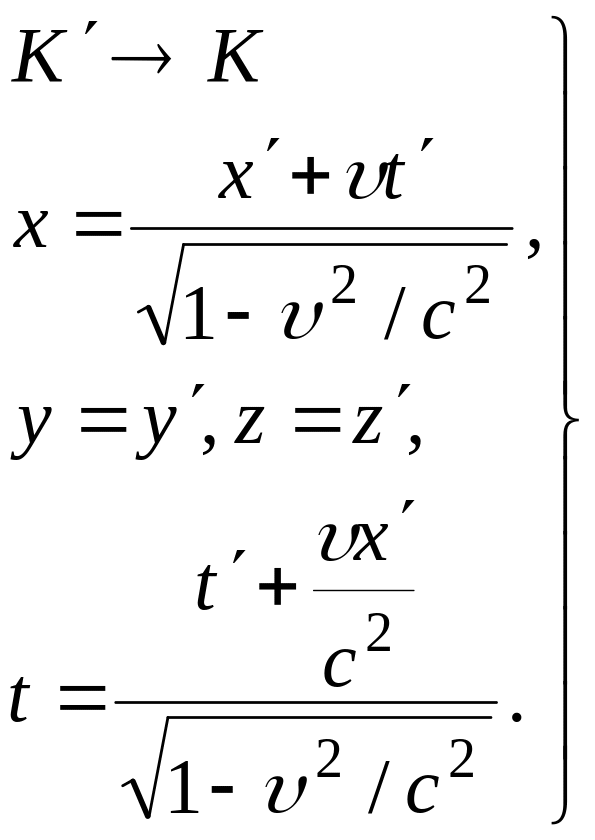(7)
(8)
Соотношения (7) и (8) носят название преобразований Лоренца.
В классической механике понятия пространства и времени являются независимыми. Из преобразований же Лоренца видна тесная связь между пространством и временем, поскольку время зависит от пространственных координат. Таким образом, в релятивистской механике рассматривается не трёхмерное пространство, к которому добавляется понятие времени, а четырёхмерное пространство с неразрывно связанными временными и пространственными координатами.
Некоторые следствия из преобразований лоренца
Из преобразований Лоренца вытекает ряд следствий, необычных с точки зрения классической механики.
1.
Предельный характер скорости света.
В классической механике считается, что
тела
могут двигаться с любыми сколь угодно
большими скоростями. Из преобразований
Лоренца, однако, следует, что
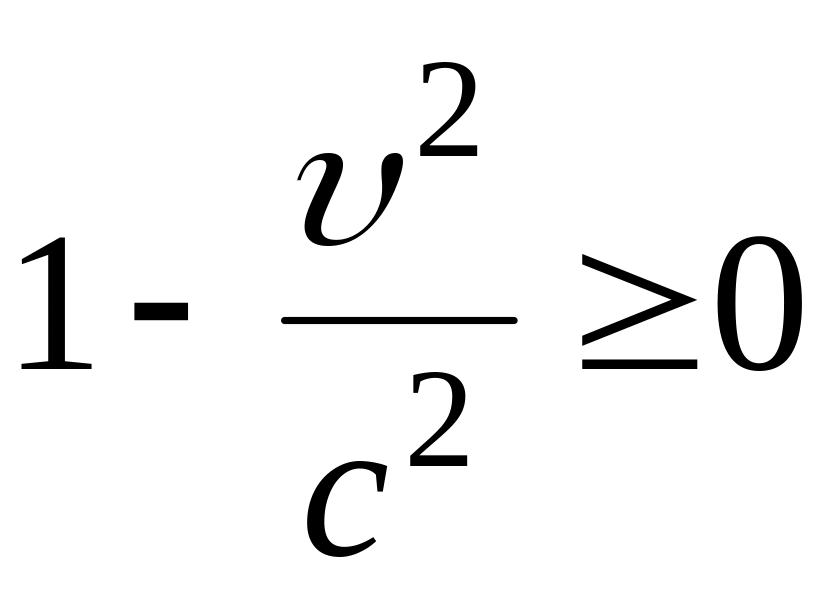(иначе
мнимый корень). Поэтому
и
т.е. скорость тела не может быть больше
скорости света в вакууме.
2. Длина тел. Рассмотрим стержень, расположенный вдоль оси абсцисс и покоящийся в системе отсчёта K. Длина стержня l в этой системе отсчёта равна l = x2 x1, где x1 и x2 координаты начала и конца стержня, не изменяющиеся со временем, так как он неподвижен. Предположим теперь, что он находится в системе отсчёта K, которая движется относительно системы K со скоростью . При этом оси абсцисс систем отсчёта совпадают. Можно показать, что длина l этого стержня с точки зрения наблюдателя, находящегося в системе отсчёта К, равна
, (9)
т.е. длина стержня, измеренная в системе отсчёта, относительно которой он движется, меньше длины, измеренной в системе, в которой он покоится. Необходимо отметить, что в направлении осей ординат и аппликат размеры стержня в данном случае не меняются.