
3.Модифицированный критерий Фурье
Для внешней задачи теплопроводности в условиях α-модели в теплообменнике сопротивление теплообмену, отнесенное к площади поверхности F1, R1=1(αF1), а сосредоточенная теплоемкость С1=сρV1. Поэтому в случае «внешней задачи» теплопередачи по формуле
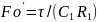 ,
,
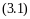
и является модифицированным критерием Фурье в рассматриваемом процессе теплообмена. Такой же результат можно получить по выражениям (2.11) и (2.13), приняв С=С1:


Решение уравнения (2.7) в результате можно записать в виде

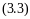
где Fo’ – пространственно-временная координата процесса втеплообменом аппарате:

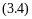
При расчете теплообменного аппарата обычно интересует установившееся распределение параметров среды в пространстве вдоль поверхности теплообмена и как результат их значения на выходе из аппарата в конце поверхности теплообмена. В такой постановке (рис.2), которая является моделью Эйлера, дифференциальное уравнение (2.6) нужно записать несколько иначе. Имея в виду, что за время τ среда продвинется со скоростью ω вдоль поверхности на расстояние x-ωτ, а dτ=dx/ω, уравнение (2.6) получим в виде
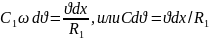

Где С=С1 ω=сρωfω=Gc – теплоемкость потока среды, G=ρωfω– ее массовый расход.
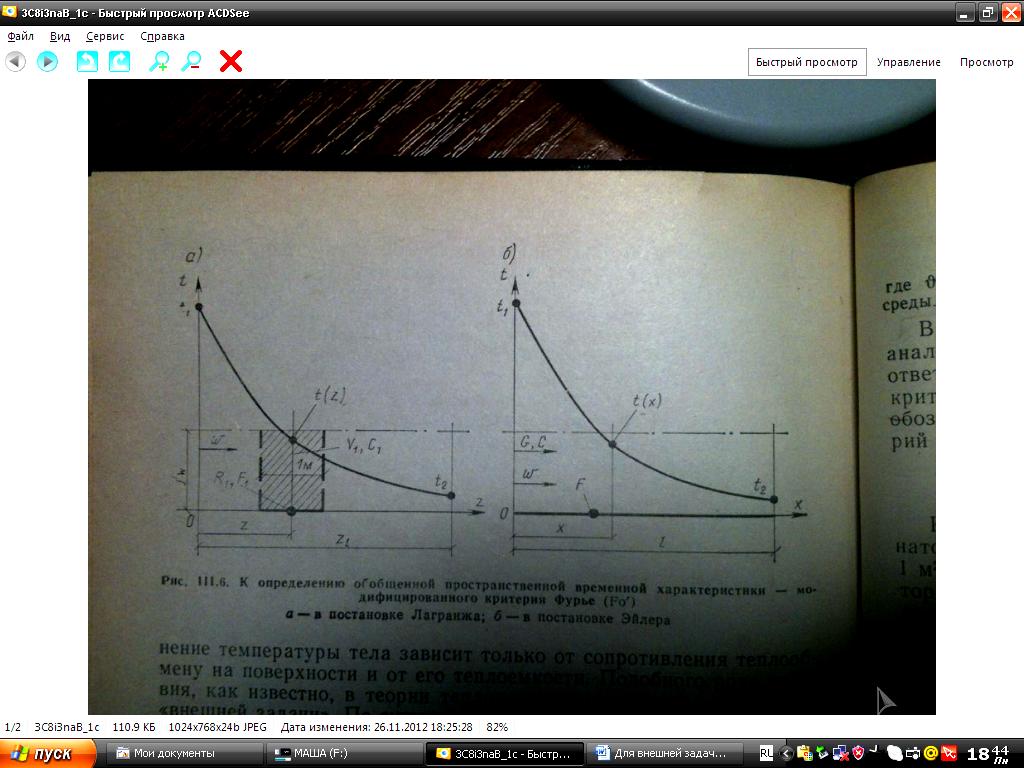
Рис.2 К определению обобщенной пространственной временной характеристики – модифицированного критерия Фурье (Fо') в постановке Эйлера.
В такой постановке решение уравнения (3.5) будет следующим:


Для условий на выходе из теплообменника (при х=l), а также при K’l=KF модифицированный критерий Fo’ будет:
 ,
,
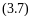
Где K’=l/R1 отнесено к 1 м длины поверхности теплообмена, а К - к 1 м2 площади поверхности теплообмена F.
Последняя запись полностью соответствует предложенному Лондоном и Кейсом и широко распространенному обозначению числа единиц переноса тепла:


Поскольку соотношение (III.76) непосредственно выводится на основе теории подобия и принятых в ней критериев подобия, представляется рациональным и логичным обозначать и называть это соотношение модифицированным критерием Фурье, а не числом единиц переноса, как это обычно делается.
Нетрудно показать, что подобным же образом могут быть получены для аппаратов теплообмена соответствующие Fo’ для условий массообмена, для условий передачи только скрытого или скрытого и явного, т.е. полного тепла.
4.Критерий Льюиса
Если считать направление процессов тепло- и массообмена положительным,если потоки тепла и массы направлены от воздуха к воде.
Для элементарных количеств тепла и вещества (водяного пара) могут быть написано следующие уравнение, если использовать коэффициент массообмена, отнесенный не к разности парциальных давлений водяного пара, а к разности влагосодержанийd:
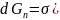 ,
,
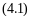
где d - влагосодержание обрабатываемого воздуха;
d" - влагосодержание воздуха, находящегося в пограничном слое(на границе воздух - вода);
а - коэффициент массообмена, отнесенный к разности влагосодержаний.
Вместе с водяным паром из воздуха к воде передается тепло, затраченноена испарение пара и теперь выделяющееся в процессе конденсации.Это тепло обычно называется «скрытым». Количествоскрытого тепла Q' можно найти из равенства
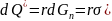 ,
,

где r- теплота испарения, выделяющаяся при конденсации водяногопара.
Полное количество тепла, которым обмениваютсявоздух и вода, составляет
 ,
,
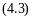
Введем очень важное соотношение, справедливое для условийподобия процессов тепло- и массопереноса, которое было полученоеще в 1922 г. Льюисом:
 ,
,
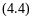
где
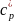 - удельная
теплоемкость влажного воздуха,
- удельная
теплоемкость влажного воздуха,
Справедливость соотношения Льюиса неоднократно подвергаласьсомнению из-за того, что при делении полученного в результате экспериментальных исследований значения коэффициента явной теплоотдачиα на коэффициент массообмена σ равенство не соблюдалось.
На
этом основании делался вывод об отсутствии
подобия процессов тепло- и массообмена
при взаимодействии воздуха и воды. Как
показано в нашей работе, получающиеся
в опытах отклонения величины
 от
объясняются не отсутствием подобияпроцессов,
а особенностями методики обработки
экспериментальных данных. Поэтому в
дальнейшем будем считать, что для каждого
элемента dFповерхности
контакта воздуха и воды справедливо
принятое Льюисом соотношение.
от
объясняются не отсутствием подобияпроцессов,
а особенностями методики обработки
экспериментальных данных. Поэтому в
дальнейшем будем считать, что для каждого
элемента dFповерхности
контакта воздуха и воды справедливо
принятое Льюисом соотношение.
Уравнение не может быть непосредственно использованы для расчета аппаратов кондиционирования воздуха,так как с его помощью определяются лишь элементарные количества тепла и водяного пара, приходящиеся на элемент поверхности контакта dF. При этом предполагается, что параметры воды и воздуха в течение контакта сохраняют постоянное значение.
Чтобы получить зависимости, с помощью которых можно было бы рассчитывать реальные аппараты, необходимо уравнение проинтегрировать по поверхности тепло- и массообмена.
Для этого надо знать:
а) форму и размеры истинной поверхности контакта F;
б) параметры воздуха и воды для каждого элемента поверхности,
а также соответствующие разности t - tx, Pn - Pп",d - d", представляющие собой движущие силы процессов.
Обычно определить оба эти фактора не представляется возможным,и поэтому приходится вводить различные допущения. Так, вместо истинных значений разностей параметров воздуха и воды используется величина средней расчетной разности, которая позволяет получить интегральные количества тепла и водяного пара, если известна истинная поверхность:
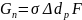 ,
,

 ,
,

где ∆d - средняя расчетная разность влагосодержаний обрабатываемоговоздуха и воздуха в пограничном слое;
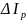 -
средняя расчетная разность энтальпий
обрабатываемоговоздухаи воздуха в
пограничном слое.
-
средняя расчетная разность энтальпий
обрабатываемоговоздухаи воздуха в
пограничном слое.
Экспериментальные исследования должны выполняться так, чтобы результаты, найденные при испытаниях того или иного аппарата, можно было распространить на все аппараты, ему подобные. Кроме того, эти результаты должны давать возможность получать обобщенные зависимости, справедливые для достаточно широких пределовусловий использования аппарата.
Обрабатывать данные опытов целесообразно, используя основныеположения теории подобия. Как известно, теория подобия позволяет вывести зависимости искомых коэффициентов переноса от величин, их определяющих, в виде так называемых критериальных уравнений. Критериальные уравнения представляют собой связи, в которых определяемые критерии (в них входят искомые коэффициентыпереноса) даются в зависимости от определяющих. Такого вида уравнения получаются в результате рассмотрения всех дифференциальных уравнений, характеризующих обстановку, в которой протекают процессы тепло- и массообмена. В общем случае это означает необходимость рассмотрения уравнений движения, неразрывности, теплопроводности и диффузии в пограничном слое, осложненных некоторыми дополнительными эффектами, а также уравнений, характеризующих граничные условия.
Как правило, использование этого хорошо известного приема непозволяет довести задачу до конца, да в этом и нет необходимости, так как из общей теории тепло- и массообмена хорошо известны текритерии подобия, которые должны входить в уравнения.
Определяемыми критериями являются:
а) для процесса теплообмена - тепловой критерий Нуссельта
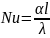 ,
,

б) для процесса массообмена - диффузионный критерий Нуссельта
 ,
,

Величина этих критериев зависит от критериев, определяющих обстановку протекания процесса, которая характеризуется гидродинамическими и термодинамическими условиями. При этом надо иметь в виду следующее.
1. Вода и воздух в тепло- и массообменных аппаратах кондиционирования воздуха находятся в чрезвычайно сложном движении. Основным гидродинамическим критерием, определяющим интенсивность тепло- и массообмена в этих условиях, является скорость относительного движения воздуха по отношению к поверхности воды. По своей природе это движение не свободное, а вынужденное. Поэтому, чтобы получить искомые зависимости и иметь возможность распространить полученные в опыте результаты, гидродинамическую обстановку процесса следует оценивать критерием Рейнольдса. При этом в расчетные зависимости нужно вводить два критерия Рейнольдса - для воздуха
Reг и воды Reж :Reг = wгl/vг и Rеж =wжl/vж. Очень часто на практике ограничиваются одним критерием Рейнольдса для воздуха и вводят в уравнения удельный расход воды, т. е. количество воды, приходящееся на единицу массы (или веса) воздуха, μ= Gж/Gг.
2. Хотя гидродинамическая обстановка процесса в основном определяетсяхарактером вынужденного движения воздуха по отношению к поверхности воды, нельзя в ряде случаев не считаться с наличием свободного движения, возникающего из-за разностей плотностей воздуха в различных точках пространства аппарата, в котором происходят тепло- и массообменные процессы.
В
теории подобия существует два критерия
для оценки влияния свободного движения:
критерий ГрасгофаGr = и критерий Архимеда Аr
=
и критерий Архимеда Аr
=
 , где γ и γ" - плотность обрабатываемого
воздуха и воздуха, находящегося в
пограничном слое над поверхностью воды.
Учитывая, что различие в плотностях
воздуха определяется не только разностью
температур, но и разностью влагосодержаний
влажного воздуха, предпочтительнее
пользоваться критерием Аr.
Однако, как показали исследования, в
условиях, в которых обычно протекают
процессы кондиционирования воздуха,
разница между этими двумя критериями
весьма мала. Поэтому при выводе расчетных
зависимостей для аппаратов кондиционирования
воздухаможно применять критерий Gr, хотя
принципиально введение критерия Аr
предпочтительнее.
, где γ и γ" - плотность обрабатываемого
воздуха и воздуха, находящегося в
пограничном слое над поверхностью воды.
Учитывая, что различие в плотностях
воздуха определяется не только разностью
температур, но и разностью влагосодержаний
влажного воздуха, предпочтительнее
пользоваться критерием Аr.
Однако, как показали исследования, в
условиях, в которых обычно протекают
процессы кондиционирования воздуха,
разница между этими двумя критериями
весьма мала. Поэтому при выводе расчетных
зависимостей для аппаратов кондиционирования
воздухаможно применять критерий Gr, хотя
принципиально введение критерия Аr
предпочтительнее.
Так обстоит дело с учетом гидродинамических факторов, которыев общем случае отражают влияние вынужденных и свободных сил. Мы пока не останавливаемся на форме учета и характере критериальных уравнений для тепло- и массообмена в обстановке одновременного действия вынужденной и свободной конвекции. Укажем, что для большинства типов установок кондиционирования воздуха влиянием свободной конвекции можно пренебречь.
3. К факторам, подлежащим учету, относятся также физические параметры паровоздушной смеси, определяющие тепловые и диффузионные процессы и оказывающие совместно с гидродинамическими факторами влияние на коэффициенты тепло- и массообмена. Это коэффициенты теплопроводности, теплоемкости, вязкости и диффузии бинарной смеси. Принято вводить два критерия, объединяющие перечисленные выше параметры: тепловой и диффузионный критерии Прандтля (Pr = v/a и Рг' = v/k).
На основании приведенного анализа особенностей процессов тепло-и массообмена в аппаратах кондиционирования воздуха можно написать в общем виде критериальные уравнения, связывающие определяемые критерии (Nu и Nu') с определяющими:
Nu
=f (Rer,Rex,Ar,Pr);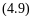
Nu'
= f '(Rег,Rеж,Аг,Рг'),
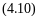
Поскольку процессы теплообмена и массообмена подобны, вид функций f и f ' должен быть вполне идентичен. Однако это не всегда бывает так, потому что при совместно протекающих процессах тепло-и массообмена наблюдается их взаимное влияние, в результате которого и возникают дополнительные эффекты. В связи с этим в правой части уравнений могут появиться дополнительные критерии, которые иногда удается получить из рассмотрения соответствующих аналитических зависимостей. Чаще дополнительные критерии получаются как результат обработки экспериментальных данных.
Явления, связанные с взаимным влиянием двух процессов переноса(тепла и вещества), можно разбить на две группы:
а) явления, происходящие в пограничном слое и таким образом влияющие на физическую природу процессов тепло- и массообмена. Сюда прежде всего относятся те дополнительные эффекты, которые определяются поперечным потоком вещества в пограничном слое. Можно считать, что для тех интенсивностей массообмена, с которыми приходится иметь дело в системах кондиционирования воздуха, влияние этих эффектов ничтожно и они могут не учитываться;
б) явления, обусловленные молярными процессами. Эти явления обычно обнаруживаются при обработке экспериментальных данных, в связи с чем и вводятся дополнительные критерии. Из числа таких критериев следует назвать температурный параметр (t-t')/T, названный критерием Гухмана (Gu) и полученный при изучении испарения жидкостей со свободной поверхности в вынужденный парогазовый поток. Из всех толкований физического смысла критерия Gu наиболее обоснованной является гипотеза А. В. Лыкова, согласно которой при движении воздуха вдоль поверхности влажного тела в пограничный слой вместе с паром попадают мельчайшие субмикроскопические частицы жидкости (молярное диспергирование) – испарение этих частиц и ведет к появлению критерия Gu.
Таким образом, критериальные уравнения, используемые для определения коэффициентов тепло- и массообмена, приобретают вид
Nu
=f (Rer,Rex,Ar,Pr,To);
Nu
' = f '(Rег,Rеж,Аг,Рг',To),

где To - температурный параметр, зависящий от характера процесса
кондиционирования.
Сравнительно небольшие пределы изменения параметров воздухаи воды в процессах кондиционирования позволяют для критериальных уравнений использовать простые степенные зависимости.
Nu
=ARermRexpArkPrnTob;
Nu
' = AlRermlRexplArklPrnlTobl,
В качестве чисел единиц переноса предлагается использовать два: число единиц переноса явного тепла (NTUя)и число единиц переноса полного тепла (NTU):
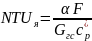 ,
,

 ,
,

где F - истинная поверхность тепло- и массообмена.
Коэффициент переноса σ является одновременно коэффициентом полного теплообмена и коэффициентом массообмена. Поэтому NTU может рассматриваться и как число единиц переноса полного тепла, и как число единиц переноса массы (водяного пара).
 ,
,
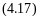
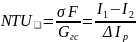 ,
,

Напишем отношение чисел единиц переноса явного и полного
тепла:
 ,
,

Учитывая полученную ранее зависимость, можем заключить, что если бы соотношение Льюиса соблюдалось для средних значений коэффициентов тепло- и массообмена, то отношение чисел единиц переноса всегда было бы равно единице. Однако, при исследовании процессов, происходящих в аппаратах кондиционирования воздуха, было выявлено нарушение соотношения Льюиса. Дадим объяснение этому нарушению, имея в виду наиболее важный процесс кондиционирования воздуха – его охлаждение и осушку.
Отклонения в величине отношения коэффициента теплообмена α к коэффициенту массообмена σ, выявленные по результатам экспериментов, отражают наблюдаемые в реальных аппаратах количественные и качественные различия поверхности теплообмена по сравнению с поверхностью массообмена. Эти отклонения закономерныи могут являться характеристикой совершенства процесса обработки воздуха (охлаждения и осушки), происходящего в реальном аппарате.
Поэтому для полной оценки тепло- и массообмена в реальныхаппаратах кондиционирования, кроме чисел единиц переноса, следует ввести дополнительную характеристику, названную нами критерием совершенства процесса:
 ,
,

Заметим, что эта характеристика внешне идентична критерию Льюиса
Le
= ,
,
применяемому при исследовании процессов сушки влажных материалов в воздухе. Однако, чтобы подчеркнуть различие в физическом смысле, мы назвали ее иначе, так как встречаются случаи, когда локальные величины Le всюду равны 1 и тем не менее ζ≠1.
