МО РБ

УО «Полоцкий государственный университет»

Кафедра теплогазоснабжения

и вентиляции

Реферат

на тему:

«Безразмерные параметры и обобщенные характеристики процесса тепло- и массообмена в аппаратах кондиционирования воздуха»

по курсу «Кондиционирование воздуха и холодоснабжение»

Выполнили: Пигалова А.В.

Богданова М.А.

Курицына И.С.

Савёлова В.О.

Ковалевская А.Н.

Кос Р.В.

Федорович М.И.

студенты гр.09 ТВ-2 Пшеничнюк В.А.

Руководитель: Нияковский А.М.

Новополоцк 2012

Содержание

1.Относительные избыточные параметры для произвольного сечения теплообменника 3

2.Определение обобщенных характеристик в простейшем случае 4

2.1.Модель Лагранжа 5

2.2.Критерии Фурье и Нуссельта 6

3.Модифицированный критерий Фурье 9

4.Критерий Льюиса 11

Список литературы: 18

Прежде, чем обратиться к рассматриваемой теме, хочется вспомнить название букв греческого алфавита, т.к. в данной теме мы часто прибегаем к их использованию.

Α α - альфа

Β β - бета

Γ γ - гамма

Δ δ - дельта

Ε ε - эпсилон

Ζ ζ – дзета (зита)

Η η – эта (ита)

Θ θ – тета (фита)

Ι ι - йота

Κ κ - каппа

Λ λ – лямбда (лямда)

Μ μ – мю (ми)

Ν ν – ню (ни)

Ξ ξ - кси

Ο ο - омикрон

Π π - пи

Ρ ρ - ро

Σ σ - сигма

Τ τ – тау (таф)

Υ υ - ипсилон

Φ φ - фи

Χ χ - хи

Ψ ψ - пси

Ω ω – омега

Для некоторых букв в скобках приведено второе название буквы. Это Новогреческое название букв рассматриваемого алфавита.

1.Относительные избыточные параметры для произвольного сечения теплообменника

Приведенные ранее зависимости позволяют определять предельные равновесные состояния рабочих сред в обменных аппаратах. Расчетные зависимости для определения равновесных состояний получены из балансовых термодинамических соотношений с использованием только условий на границах системы.

Поскольку аппарат имеет конечные размеры, то рабочие тела выходят из теплообменника с параметрами, занимающими некоторое промежуточное положение между параметрами на входе в теплообменник и параметрами в предельном равновесном состоянии. Следовательно, процесс тепло- и массопереноса в теплообменниках можно рассматривать как переходный от некоторого неравновесного начального состояния к промежуточному относительно предельного равновесного состояния.

2.Определение обобщенных характеристик в простейшем случае

В связи с этим оказывается, что при расчете теплообменника удобно пользоваться безразмерными параметрами тепло- и массообменивающихся сред обобщенными характеристиками переходного процесса , как это делается при расчете переходных процессов нестационарной теплопередачи. Относительные избыточные параметры для произвольного сечения теплообменника будут:

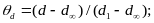
где t, d, I- текущие параметры рабочей среды в произвольном сечении; , , ; 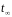, , 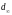-начальные и предельные равновесные параметры рабочей среды.

Значение на входе рабочих сред в теплообменник равна (для каждой из сред), а бесконечной продолжительности контакта или длине поверхности контакта в предельном равновесном состоянии стремиться к 0. Обычно при расчетах определяется некоторое промежуточное значение параметра 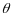на выходе из аппарата. Относительное избыточное значение этого конечного параметра, например, , будет:

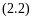
где 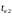и - температура в конце аппарата и при предельном равновесном состоянии.

Такая форма записи безразмерного параметра 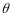далее называется вариантом А.

Иногда более удобно оказывается запись безразмерного параметра относительно разности начальных параметров обменивающихся сред:

Эта форма записи в дальнейшем будет называться вариантом Б.

2.1.Модель Лагранжа

Для определения характера изменения параметров рабочих сред в теплообменнике необходимо решить дифференциальные уравнения, из которых можно получить и другие обобщенные характеристики процесса, также пользуясь методами, применяемыми в теории теплопередачи.

Если тело имеет достаточно большую теплопроводность и небольшой коэффициент теплообмена на границе с окружающей его средой, то при нагревании или охлаждении в толще тела наблюдается сравнительно равномерное распределение температуры. Изменение температуры тела зависит только от сопротивления теплообмену на поверхности и от его теплоемкости. Подобного рода условия, как известно, в теории теплопередачи относят к категории «внешней задачи».

Рис.1 К определению обобщенной пространственной временной характеристики – модифицированного критерия Фурье (Fо') в постановке Лагранжа.

Для определения обобщенных характеристик рассмотрим постановку и решение задачи теплообмена для ТП-модели в простейшем случае, когда одна среда контактирует с поверхностью , температура которой задана (рис). Вначале рассмотрим постановку и решение задачи в вид модели Лагранжа (см. рис) относительно элемента объема среды, который движется вдоль поверхности и изменяет при этом свою температуру во времени z. Теплоемкость 1 м такого элемента, Дж/град, объемом V₁ определим зависимостью:

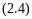
где 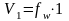(здесь площадь 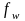поперечного сечения канала, по которому движется среда; 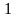- длина элемента движущейся среды, м).

Сопротивление теплообмену на поверхности элемента объема среды, 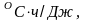при его длине 1 м:

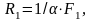
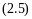
где 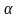- коэффициент теплообмена на поверхности; - площадь поверхности теплообмена на длине 1 м.

Дифференциальное уравнение изменения температуры элемента объема среды во времени 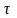, по мере продвижения вдоль поверхности теплообмена, можно записать в виде:

_{где ϑ= t – tпов- текущая избыточная относительно tповтемпература среды.}

Решение этого уравнения можно записать в виде относительной избыточной температуры среды θ:

_θ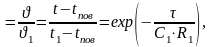

_{гдеϑ1= t – tпов– избыточная относительно tповначальная (t1) температура среды.}