3.5. Правило Лопиталя
Правило
Лопиталя (см. разд. 2.11) применяется для
раскрытия неопределенностей типа
и
.
В
случае неопределенности типа
или
следует алгебраически преобразовать
данную функцию так, чтобы привести ее
к неопределенности типа
или
и далее воспользоваться правилом
Лопиталя. В случае неопределенности
типа
,
,
,
следует прологарифмировать данную
функцию и найти предел ее логарифма.
Пример
1. Найти
.
Решение.
Так как при
функции
и
,
то имеем
неопределенность типа
.
Числитель и
знаменатель данной дроби непрерывны,
дифференцируемы и стремятся к нулю. Это
означает, что можно применить правило
Лопиталя:
.
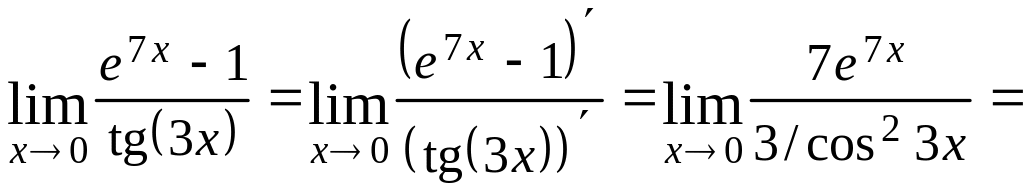
Пример
2. Найти
.
Решение.
.
В данном случае после применения правила Лопиталя были использованы основные теоремы о пределах и первый замечательный предел.
Пример
3. Найти
.
Решение.
.
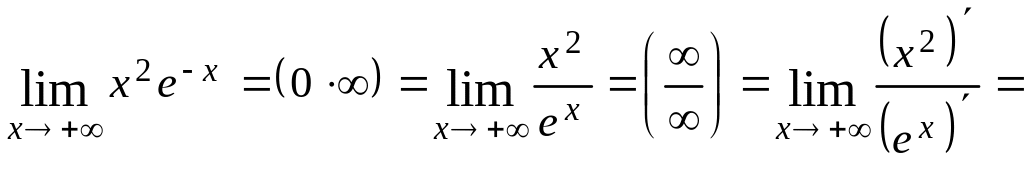
Пример
4. Найти
.
Решение.
.
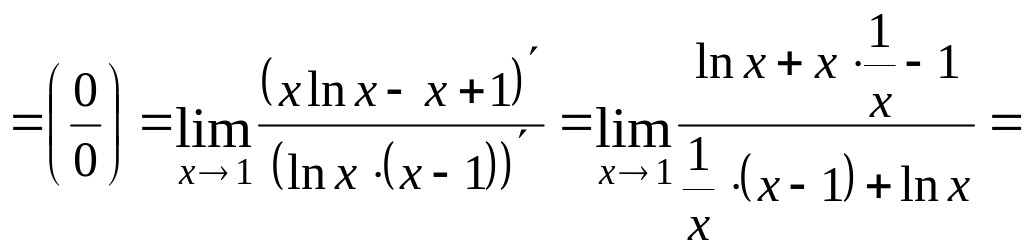
Пример
5. Найти
.
Решение. В данном случае имеем неопределенность типа , поэтому для раскрытия этой неопределенности применим метод логарифмирования.
Пусть
.
Тогда с учетом того, что логарифмическая
функция непрерывна, имеем
.
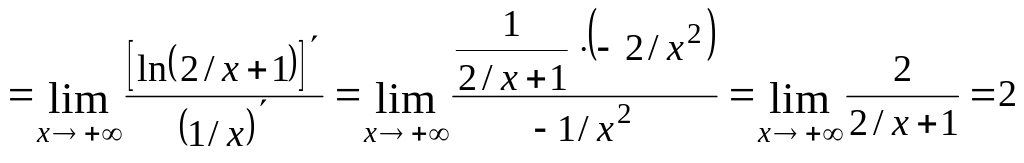Так
как
,
то
.
Пример
6. Найти
.
Решение.
Так как имеем
неопределенность типа
,
то введем обозначение
,
тогда
.
Поскольку
,
то
.
3.6. Исследование функций и построение их графиков
При
полном исследовании функции
и построении ее графика можно придерживаться
следующей схемы:
указать область определения функции;
исследовать функцию на симметричность;
найти точки пересечения графика функции с осями координат;
найти точки разрыва функции;
определить уравнения асимптот графика функции;
найти критические точки первого рода;
исследовать функцию на монотонность и экстремумы;
найти критические точки второго рода;
определить интервалы выпуклости и вогнутости, точки перегиба;
произвести необходимые дополнительные вычисления;
построить график функции.
Дадим пояснения к каждому пункту приведенной схемы.
1)
Если каждому элементу
по определенному правилу
поставлен
в соответствие единственный элемент
,
то говорят, что задана функция
,
где
называется независимой переменной или
аргументом.
Множество
называется областью определения функции.
Поэтому, чтобы найти
,
нужно определить множество точек
действительной оси, для которых правило
имеет смысл и определяет действительные
значения переменной
.
2)
Если для любого
из области определения
выполняется равенство
,
то функция является четной, если же
выполняется равенство
,
то функция является нечетной. В том
случае, когда
и
- функция не является ни четной, ни
нечетной.
Четные
и нечетные функции называются
симметричными, так как график четной
функции симметричен относительно оси
,
а график нечетной – относительно начала
координат. Таким образом, график
симметричной функции достаточно
построить лишь для
,
а потом, используя симметрию, достроить
его на оставшейся части области
определения.
3)
Точки пересечения графика функции
с осью
определяются из условия
,
т.е.
;
точка пересечения с осью
определяется из условия
,
значит,
.
4)
Функция
называется непрерывной при
(в точке
),
если:
а)
функция
определена в точке
и ее окрестности;
б) существует конечный предел функции в точке ;
в)
этот предел равен значению функции в
точке
,
т.е.
.
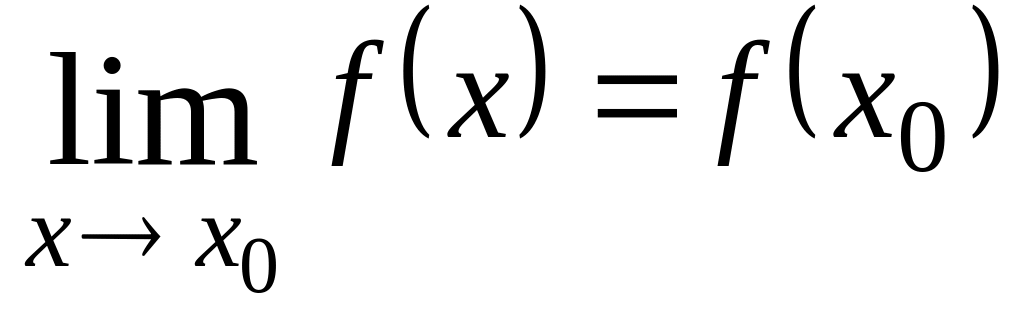Точка
,
в которой нарушено хотя бы одно из трех
условий непрерывности функции, называется
точкой разрыва функции. Если в точке
разрыва
существуют конечные пределы
и
,
то
называется точкой разрыва первого рода.
Если хотя бы один из пределов
или
не существует или равен бесконечности,
то точку
называют точкой разрыва второго рода.
5)
Прямая l
называется
асимптотой данной кривой
,
если расстояние от точки
кривой до прямой
l
при удалении точки
от начала координат на бесконечность
стремится к нулю. Различают вертикальные,
наклонные и горизонтальные асимптоты.
Прямая
является
вертикальной асимптотой графика функции
,
если
,
или
.
Таким
образом, вертикальные асимптоты
появляются в том случае, когда существуют
точки разрыва второго рода
(точки бесконечного разрыва функции),
и в некоторых случаях, если
– граница интервала области определения
функции
.
Прямая
является наклонной асимптотой графика
функции
,
если существуют конечные пределы
,
или
,
.
В
частности, при
получаем
или
.
Полученная
прямая
является горизонтальной асимптотой
графика функции
.
6)
Функция
называется возрастающей (убывающей) в
некотором интервале
,
если большему значению аргумента из
этого интервала соответствует большее
(меньшее) значение функции, т.е. при
выполняется неравенство
.
Интервалы, в которых функция возрастает или убывает, называются интервалами монотонности функции. Интервалы возрастания и убывания функции отделяются друг от друга точками экстремума или точками, выпадающими из области определения .
Необходимое
условие существования экстремума
функции: если функция
в точке
имеет экстремум, то производная
обращается в нуль или не существует.
Точки, в которых
(стационарные
точки) или
не существует, называются критическими
точками первого рода.
7)
Для нахождения интервалов монотонности
функции
необходимо воспользоваться тем фактом,
что если для любого
из интервала
,
то функция возрастает на этом интервале
,
если
,
то функция убывает на этом интервале.
Точки экстремума следует искать среди критических точек первого рода. И, так как не во всякой критической точке достигается экстремум функции, то для его нахождения каждую критическую точку (в отдельности) следует исследовать с помощью одного из двух достаточных признаков существования экстремума.
Первый достаточный признак существования экстремума. Пусть – критическая точка первого рода.
Если
при произвольном, достаточно малом
выполняются неравенства:
,
(при переходе через критическую точку
производная меняет знак с плюса на
минус), то функция
в точке
имеет максимум.
Если
,
(при переходе через точку
производная меняет знак с минуса на
плюс), то функция
в точке
имеет минимум; если
,
или
,
(производная знака не меняет), то функция
в точке
экстремума не имеет.
Второй
достаточный признак существования
экстремума. Если
– критическая точка первого рода и
,
то функция в точке
имеет экстремум, а именно: максимум,
если
,
и минимум, если
.
8)
Необходимое условие существования
точки перегиба: если
– точка перегиба
графика
функции
,
то
вторая производная
или
не
существует.
Точки, в которых или не существует, называются критическими точками второго рода.
9)
График функции
называется выпуклым на интервале
,
если он расположен ниже касательной,
проведенной в любой точке этого интервала.
График функции
называется вогнутым на интервале
,
если он расположен выше касательной,
проведенной в любой точке этого интервала.
Точка кривой
,
отделяющая выпуклую ее часть от вогнутой,
называется точкой перегиба кривой.
Не всякая критическая точка второго рода является точкой перегиба графика функции. Поэтому каждую критическую точку необходимо исследовать при помощи достаточного признака существования точки перегиба: если - критическая точка второго рода и при произвольном достаточно малом выполняются неравенства
,
или
,
(при переходе через критическую точку вторая производная меняет знак), то является точкой перегиба графика функции.
Если на интервале , то график функции является выпуклым на этом интервале, если же , то на этом интервале график функции вогнутый.
10) Необходимо вычислить значения функции в точках экстремума и в точках перегиба графика функции. Если информации для построения графика недостаточно, найти значения функции в произвольно выбранных вспомогательных точках.
Результаты, полученные во всех предыдущих пунктах для наглядности можно оформить в виде таблицы. Эта таблица заполняется следующим образом:
а) в первой строке указываются интервалы, на которые все критические точки разбивают числовую ось и сами точки;
б) во второй строке указываются знаки первой производной на этих интервалах, в третьей строке - знаки второй производной;
в)
в четвертой строке схематически
указывается характер поведения функции.
Например, если
и
,
то функция возрастает, а график является
вогнутым. По этой таблице совсем нетрудно
построить график функции, для этого
нужно последнюю строку перенести в
декартову систему координат в подходяще
выбранном масштабе.
Пример
1. Исследовать
методами дифференциального исчисления
функцию
и построить ее график.
Решение
1)
Областью определения функции является
вся числовая ось, за исключением точек,
в которых знаменатель дроби обращается
в нуль, то есть
.
Отсюда
,
,
.
Итак, область определения
.
2)
Найдем
:
,
так как , то функция является нечетной, и ее график симметричен относительно начала координат.
3) Точка пересечения с осью определяется равенством , т.е.
,
.
Точка пересечения с осью определяется равенством :
,
т.е.
.
Итак, график функции имеет единственную
точку пересечения с осями координат –
начало координат
.
4) Так как при и не выполняется первое условие непрерывности функции в точке, то эти точки являются точками разрыва функции . Причем эти точки являются точками разрыва второго рода, так как
, 
и
, 
.
5)
Так как данная функция имеет точки
разрыва второго рода (точки бесконечного
разрыва функции), то существуют
вертикальные асимптоты графика функции
и их уравнения:
и
.
Найдем уравнения невертикальных асимптот, для этого вычислим коэффициенты в уравнении прямой :
,
.
Следовательно,
прямая
является наклонной асимптотой при
и
.
6)
Найдем производную
:
.
Для
того чтобы найти критические точки
первого рода, решим уравнение:
и выясним, в каких точках не существует
.
Уравнение
равносильно уравнению
или
,
отсюда находим стационарные точки:
,
,
.
Производная не существует в том случае,
когда знаменатель
,
т.е. при
,
.
Таким образом, получили пять критических
точек первого рода:
,
,
,
,
.
7
)
Для нахождения экстремумов и интервалов
монотонности функции на числовой прямой
отметим все критические точки и определим
знак производной в каждом из получившихся
интервалов.
Д
ля
этого достаточно взять по одной
произвольной точке из каждого интервала
и вычислить значения производной (рис.
3.2).
Например:
; 
;
;
;
;
.
Так
как при переходе через критические
точки
производная меняет знак, то эти точки
являются точками экстремума функции.
В частности, при
достигается минимум функции, а при
– максимум. Кроме того, на интервалах
и
функция возрастает, а на интервалах
,
и
– убывает.
8)
Найдем
:
.
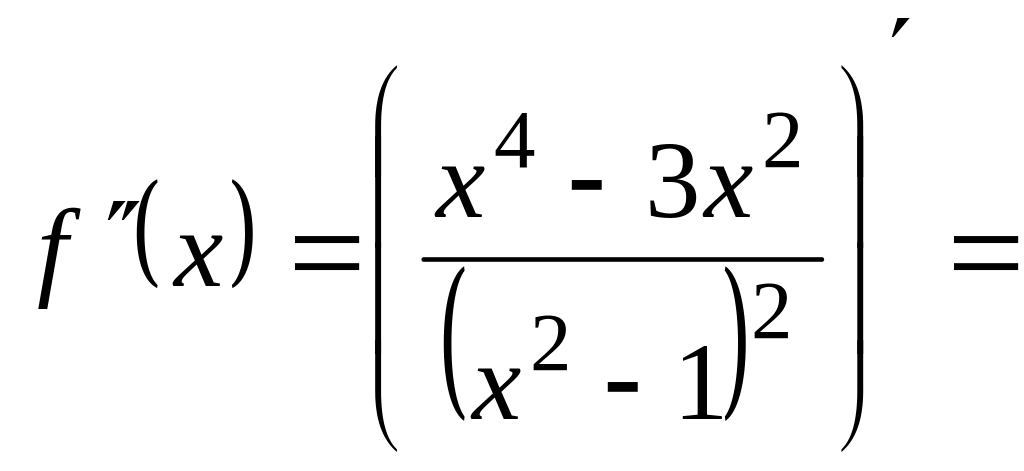
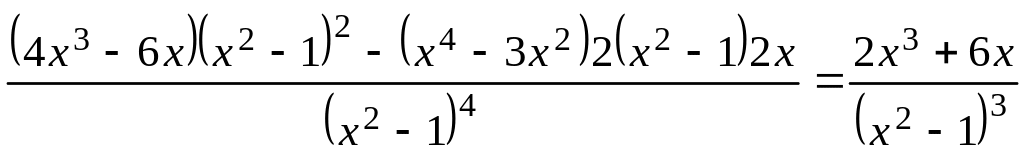Определим критические точки второго рода. Приравняем вторую производную к нулю:
,
это
уравнение равносильно уравнению
,
откуда
.
Производная
второго порядка не существует при
.
В итоге получили три критические точки
второго рода:
,
,
.
9) На числовой оси отложим все критические точки второго рода и определим знаки второй производной аналогично тому, как это сделано в пункте 7 (рис. 3.3):
,
,
,
.
П
ри
переходе через точку
вторая производная меняет знак,
следовательно,
– точка перегиба графика функции. На
интервалах
и
график функции является выпуклым, а на
интервалах
и
– вогнутым.
10) Вычислим значения функции в точках экстремума и перегиба:
, 
, 
.
Для
более точного построения графика найдем
значения функции в дополнительных
точках:
, 
.
11) Полученные данные занесем в таблицу:.
|
0 |
(0, 1) |
1 |
|
|
|
|
0 |
– |
|
– |
0 |
+ |
|
0 |
– |
|
+ |
+ |
+ |
|
|
|
|
|
|
|
Теперь построим график функции (рис. 3.4).
П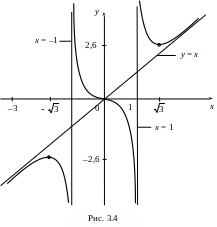
ример
2. Исследовать
методами дифференциального исчисления
функцию
и построить ее график.
Решение
1)
Исходя из того, что известны области
определения элементарных функций
и
,
получаем область определения функции:
:
.
2) Так как функция определена только для положительных значений , то функция не является симметричной.
3)
Найдем точки пересечения с осью
:
или
,
т.е.
,
откуда
.
Точки пересечения с осью
не существует, так как
никогда не обращается в нуль. Поэтому
график функции пересекается с осями
координат в единственной точке –
.
4) Данная функция непрерывна на всей области определения.
5) Изучим поведение функции на левом конце области определения, для этого вычислим предел:
.
Отсюда прямая (ось ) является вертикальной асимптотой к графику функции.
Найдем уравнения невертикальных асимптот. Для этого вычислим (используя правило Лопиталя) следующие пределы:
,
.
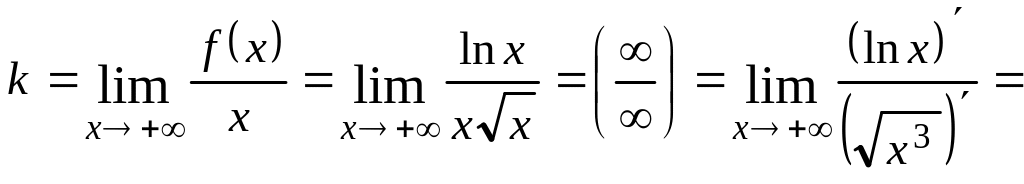
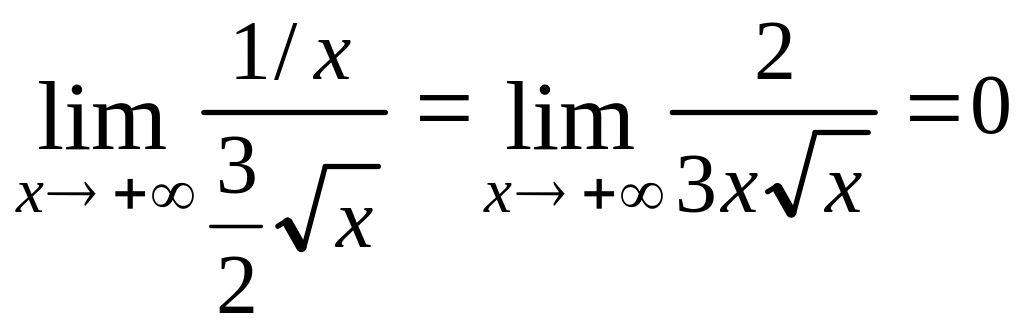Полученная прямая (ось ) является горизонтальной асимптотой графика функции.
6)
Найдем
:
.
Производная
равна нулю, когда
,
то есть при
.
Производная существует на всей области
определ
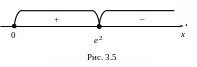ения
функции
.
Следовательно, существует только одна
критическая точка первого рода.
7) Нанесем область определения и критическую точку на числовую ось и найдем знаки производной на всех интервалах (рис. 3.5):
,
.
Так
как при переходе через критическую
точку производная меняет знак, то
– точка экстремума функции (точка
максимума). На интервале
функция возрастает, а на
– убывает.
8)
Найдем
:
.
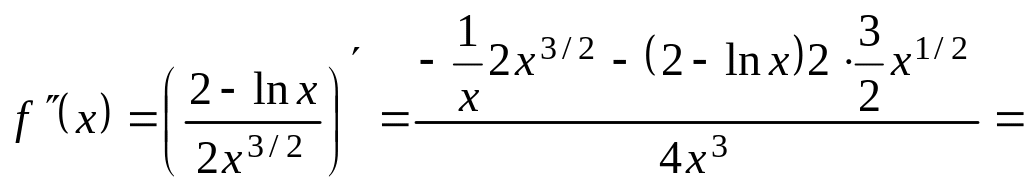
Производная
второго порядка равна нулю, если
или
,
.
Отсюда получаем:
,
.
Так как
не входит в область определения функции,
то существует только одна критическая
точка второго рода
.
9) Нанесем область определения функции и критическую точку второго рода на числовую ось (рис. 3.6). Найдем знаки на всех полученных интервалах:
,
.
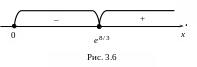При
переходе через критическую точку
производная второго порядка сменила
знак, следовательно, это точка перегиба
графика функции. На интервале
график является выпуклым, а на
– вогнутым.
10) Найдем значения функции при и :
,
.
Для
более точного построения графика
вычислим значения функции
в дополнительной точке:
.
11) Данные, необходимые для построения графика, сводим в таблицу и согласно последней строке в таблице строим график функции (рис. 3.7).
|
|
|
|
|
|
|
+ |
0 |
– |
– |
– |
|
– |
– |
– |
0 |
+ |
|
|
|
|
|
|
