Лекция 1. Статистическое описание с позиции классической механики. Функция распределения. Статистическое усреднение. Флуктуации аддитивных величин.

Составляя уравнения движения механической системы и интегрируя их, мы принципиально можем получить исчерпывающие сведения об эволюции механической системы. Однако когда мы попытаемся применить методы механики к макроскопической системе, т.е. системе с колоссальным порядка числа Авогадро числом степеней свободы, мы столкнемся с необходимостью составить и решить столь же гигантское число дифференциальных уравнений, что представляется, вообще говоря, невозможным на практике. Следует отметить, что даже если мы получим общее решение уравнений движения такой системы, то совершенно невозможно будет подставить в это решение начальные условия.

Таким образом, нет никакой возможности дать полное механическое описание эволюции состояния макроскопической системы, даже в том случае, когда она замкнута.

Однако, к счастью, для описания подавляющего числа явлений, связанных с макрообъектами, достаточно знать только макроскопические величины, т.е. величины, характеризующие не отдельные частицы, а все тело или его отдельные макроскопические части. Такие величины обладают весьма замечательным свойством.

Из опыта известно, что если макроскопическое тело поместить в стационарные условия, то по истечении некоторого времени (времени релаксации) оно придет в состояние термодинамического равновесия. Это состояние характеризуется тем, что все макроскопические величины подавляющую часть времени являются практически постоянными и лишь сравнительно очень редко испытывают сколько-нибудь заметные отклонения. Причем данное обстоятельство тем более справедливо, чем сложнее и больше рассматриваемое тело. Указанный характер поведения макроскопических величин позволяет при описании таких систем вместо истинной зависимости этих величин от времени использовать их средние по времени значения. Для величины это среднее дается стандартным выражением

. (1)

Статистическая физика представляет собой математический аппарат, который позволяет вычислять эти средние, не прибегая при этом к указанной формуле. Легко понять что, с помощью этой формулы совершенно нельзя сделать никакие теоретические предсказания значений термодинамических характеристик. Для того, чтобы вычислить среднее с помощью этой формулы, нужно вначале определить зависимость от времени механического состояния системы, т.е. зависимость от времени всех обобщенных координат и скоростей, что невозможно на практике из-за колоссального числа степеней свободы. К счастью оказывается, что как раз наличие у макроскопической системы колоссального числа степеней свободы позволяет вычислять такие средние, не прибегая к этому непосредственному определению.

Прежде, чем перейти непосредственно к обсуждению способов вычисления этих средних, договоримся о некоторой терминологии. Прежде всего, механическое состоянии системы будем называть ее микросостоянием.

Далее введем понятие фазового пространства механической системы. Каждое микросостояние системы с степенями свободы может быть математически представлено в виде точки в воображаемом -мерном пространстве, по координатным осям которого откладываются обобщенные координаты и импульсы. Это воображаемое -мерное пространство называется фазовым пространством системы. Каждая точка фазового пространства отвечает определенным значениям координат и импульсов системы и изображает собой определенное состояние механической системы. С течением времени состояние системы изменяется и соответственно точка фазового пространства, изображающая состояние системы, будет описывать в нем некоторую кривую, которая называется фазовой траекторией. В дальнейшем, когда я буду говорить, что система находится в данной точке фазового пространства, то я буду иметь ввиду, что система находится в состоянии, которому отвечает эта точка фазового пространства. Также договоримся запись обозначать просто . Аналогично, запись будем обозначать . Тогда элементарный объем фазового пространства будет обозначаться .

Приступим теперь к рассмотрению вопроса о том, как можно вычислять статистические средние макроскопических величин, не решая при этом полную механическую задачу

Прежде всего заметим, что макроскопические тела, с которыми нам приходится иметь дело, являются относительно малыми частями большой замкнутой системы, состоящей из внешних тел вместе со средой, в которую они погружены. Например, в случае макроскопического тела, помещенного в термостат, это тело вместе с термостатом образует замкнутую систему. При этом изучаемая нами система очень мала по сравнению с термостатом, так что влияние нашей системы на термодинамическое состояние термостата пренебрежимо мало.

Поэтому постановка нашей задачи должна быть следующей. Рассмотрим замкнутую макроскопическую систему, т.е. систему, не взаимодействующую ни с какими другими телами. Выделим в этой системе некоторую ее часть, которая с одной стороны весьма мала по сравнению со всей системой, а с другой стороны также является макроскопической. Такие относительно малые, но при этом макроскопические части мы будем называть подсистемами. Наша цель состоит в том, чтобы научиться вычислять средние по времени значения макроскопических величин для этих подсистем, не прибегая к решению полной механической задачи. Подсистема сама является макроскопической системой, но при этом уже отнюдь не замкнутой. Напротив, она испытывает всевозможные воздействия со стороны остальных частей системы. Из-за наличия у этих остальных частей системы большого числа степеней свободы эти взаимодействия будут иметь весьма сложный и запутанный характер. Поэтому микросостояние подсистемы будет меняться со временем весьма сложным и запутанным образом. Как раз этот сложный и запутанный характер эволюции микросостояния подсистемы и позволяет подойти к решению поставленной задачи с другой стороны.

В основе этого подхода лежит то обстоятельство, что благодаря сложному и запутанному характеру эволюции микросостояния нашей подсистемы, она за достаточно большой промежуток времени успеет побывать достаточно большое число раз во всех возможных своих микросостояниях. Точнее это обстоятельство можно сформулировать следующим образом. Выделим достаточно малый объем фазового пространства . Можно утверждать, что за достаточно большой промежуток времени наша подсистема достаточно много раз пройдет через этот объем фазового пространства. Пусть - часть полного времени , в течении которого наша подсистема находится в точках данного объема фазового пространства. При неограниченном увеличении полного времени отношение будет стремиться к некоторому конечному пределу

. (2)

Этот предел можно, очевидно, рассматривать как вероятность того, что при наблюдении нашей подсистемы в некоторый произвольный момент времени мы обнаружим ее находящейся в данном участке фазового пространства.

Переходя к бесконечно малым элементам фазового пространства, мы можем определить вероятность состояний, которые изображаются точками внутри элементарного фазового объема, т.е. вероятность того, что обобщенные координаты и импульсы лежат в заданных интервалах между , и , . Эту вероятность можно представить в виде

. (3)

Функция зависит от всех координат и импульсов подсистемы и играет роль плотности вероятности нахождения подсистемы в данной точке ее фазового пространства. Эта функция называется функцией статистического распределения или, как часто говорят, просто функцией распределения.

Функция распределения, очевидно должна удовлетворять условию нормировки

, (4)

где интеграл берется по всему фазовому пространству подсистемы. Условие нормировки есть просто отражение того простого факта, что вероятность того, что подсистема в любой момент времени обязательно находится в каком-то своем микросостоянии.

Вычисление этой функции распределения как раз и является основной задачей статистической теории. Оказывается, что функцию распределения можно найти, не решая полную механическую задачу.

Зная функцию распределения, мы сразу можем вычислить вероятности различных значений любой физической величины , зависящей от микросостояния данной подсистемы (т.е. от значений ее координат и импульсов ). Соответственно, мы также можем вычислить и среднее значение любой такой величины. Оно получатся путем умножения всех возможных значений данной величины на соответствующие вероятности и интегрирования по всем состояниям. Другими, словами среднее значение величины дается формулой

, (5)

где интегрирование ведется по всему фазовому пространству данной подсистемы.

В силу своего определения вероятности, с помощью формулы (3), усреднение с помощью функции распределения, или как говорят, статистическое усреднение полностью эквивалентно усреднению по времени (1). Однако статистическое усреднение обладает тем преимуществом, что оно освобождает нас от необходимости следить за изменением истинного значения физической величины со временем.

Следует отметить, что статистическая теория не дает такой исчерпывающе полной и однозначной информации о системе, какую дают методы классической механики. Выводы и предсказания статистической теории в отличие от результатов классической механики имеют вероятностный характер. Причем вероятностный характер результатов статистической теории сам по себе отнюдь не лежит в самой природе рассматриваемых ею объектов, он есть лишь следствие того, что эти результаты получаются на основании гораздо меньшего количества данных, чем это нужно было бы для полного механического описания (не требуются начальные значения всех координат и импульсов).

Тем не менее, при практическом применении статистической теории к макроскопическим телам в состоянии термодинамического равновесия ее вероятностный характер обычно совершенно не проявляется. Дело в том, что, как уже обсуждалось, если наблюдать любое макроскопическое тело, находящееся в состоянии термодинамического равновесия, в течение достаточно большого промежутка времени, то окажется, что все характеризующие тело макроскопические величины являются практически постоянными и лишь сравнительно очень редко испытывают сколько-нибудь заметные отклонения. В терминах статистического распределения это означает, что если с помощью функции распределения построить функцию распределения вероятностей различных значений величины , то эта функция будет иметь чрезвычайно резкий максимум при , будучи сколько-либо заметно отличной от нуля лишь в самой непосредственной близости к точке максимума (рис.1).

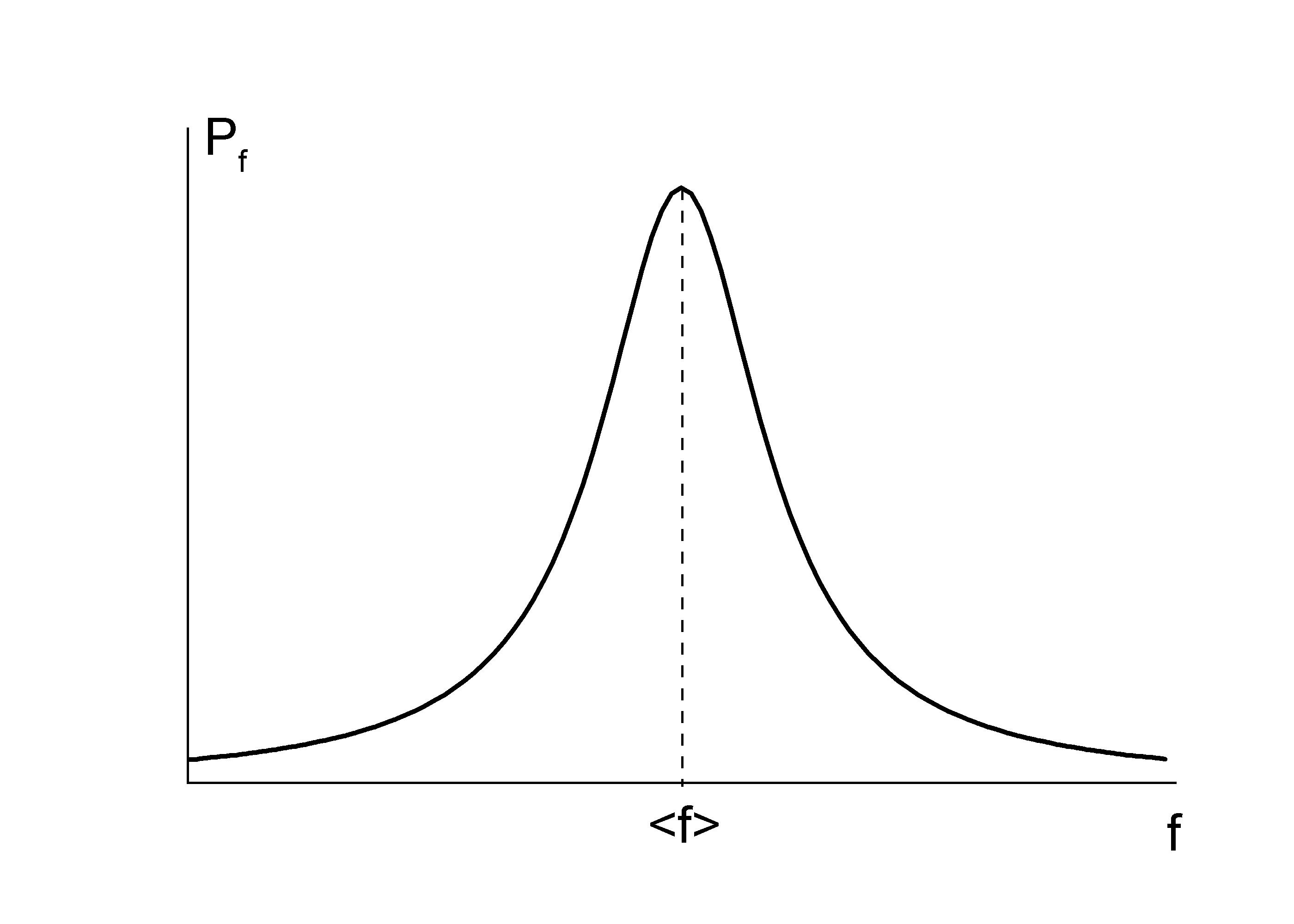
Рис.1.

Таким образом, давая возможность вычислять средние значения величин, характеризующих макроскопические тела, статистическая теория тем самым позволяет делать предсказания, оправдывающиеся с весьма большой точностью для подавляющей части времени наблюдения. В этом смысле предсказания статистики приобретают практически определенный, а не вероятностный характер.

Далее, обратим внимание на тот факт, что энергия взаимодействия макроскопической системы со своим окружением существенно меньше ее внутренней энергии. В самом деле, во взаимодействии подсистемы с окружающими частями большой системы в основном принимают участие частицы, находящиеся вблизи ее поверхности. Относительное число частиц вблизи поверхности по сравнению с полным числом частиц в подсистеме быстро уменьшается с ростом размеров системы, и при достаточной большой величине подсистемы энергия ее взаимодействия со своим окружением будет существенно меньше внутренней энергии подсистемы. Такое соотношение между энергией взаимодействия подсистем и их внутренней энергией, во-первых, служит обоснованием того, что функция распределения данной подсистемы зависит только от ее координат и импульсов, и не зависит от микросостояния ее окружения. Кроме того, указанное обстоятельство дает возможность считать подсистемы независимыми в статистическом смысле.

Остановимся здесь более подробно. Рассмотрим каких-либо две подсистемы. Первую подсистему обозначим цифрой 1, втору цифрой – 2. Будем обозначим обобщенные координаты и импульсы первой подсистемы и . Обобщенные координаты и импульсы второй подсистемы будем, соответственно, обозначать и . Функция распределения первой подсистемы зависит только от ее координат и импульсов и , и не зависит от микросостояния окружающей ее среды. В частности, она не зависит от координат и импульсов и второй подсистемы. Функция распределения второй подсистемы также зависит только от ее координат и импульсов и и не зависит от микросостояния окружающей ее среды. В частности, она не зависит от и . Функция распределения составной подсистемы “1+2”, т.е. подсистемы, представляющей собой объединение подсистемы 1 и подсистемы 2, зависит только от , , и и не зависит от координат и импульсов остальных частей большой замкнутой системы. Рассмотрим два события. Первое событие состоит в том, что подсистема 1 находится в объеме ее фазового пространства, который окружает точку . Второе событие состоит в том, что подсистема 2 находится в объеме ее фазового пространства, который окружает точку . Так вот, эти два события являются независимыми с точки зрения теории вероятности, т.е. вероятность того, что оба эти события произойдут одновременно, равна произведению вероятности первого события и вероятности второго события. Другими словами, вероятность того, что составная система “1+2” находится в элементе ее фазового пространства , который окружает точку , равна произведению вероятности первой системе находиться в элементарном объеме ее фазового пространства и вероятности второй системе находиться в элементарном объеме ее фазового пространства. Таким образом, мы можем написать

, (6)

Из написанного равенства непосредственно следует, что

, (7)

т.е. функция распределения составной подсистемы “1+2” равна произведению функций распределения подсистемы 1 и подсистемы 2.

Аналогичное соотношение можно написать и для совокупности нескольких подсистем, при условии, конечно, что совокупность всех этих подсистем все еще составляет малую часть замкнутой системы.

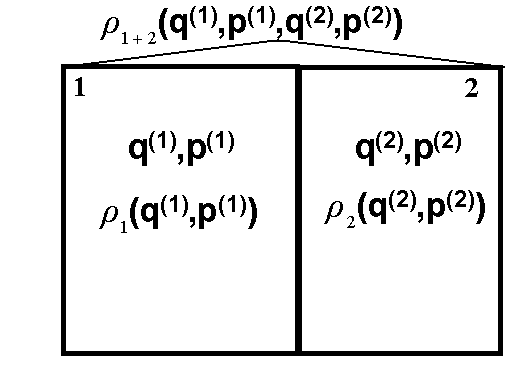
Рис.2

Можно, очевидно, утверждать и обратное, если распределение вероятностей сложной системы распадается на произведение множителей, каждый из которых зависит только от микросостояния одной из ее, то это значит, что эти части статистически независимы, причем каждый из множителей пропорционален вероятности состояний соответствующих подсистем.

Теперь рассмотрим какую-либо величину , относящуюся ко всему изучаемому телу или его отдельной макроскопической части. Эта величина будет с течением времени изменяться, колеблясь около своего среднего значения. Введем величину, характеризующую в среднем ширину интервала этого изменения. На первый взгляд, казалось бы, в качестве такой характеристики следует взять среднее значение разности между самой величиной и ее средним значением. Однако среднее этой разности служить такой характеристикой не может, поскольку для макроскопической системы это среднее всегда равно нулю, независимо от того сколь часто наша величина значительно отклоняется от своего среднего значения. Действительно, по определению среднее значение нашей разности есть

. (8)

Подставляем явный вид нашей разности . В результате получаем

Отсюда

. (9)

Оставшийся интеграл равен единице в силу условия нормировки функции распределения. Таким образом, получаем, что среднее нашей разности

(11)

всегда равно нулю, не зависимо от того, как ведет себя наша величина .

В свете сказанного понятно, что в качестве искомой характеристики удобно брать среднее значение квадрата этой разности . По определению это среднее есть

. (12)

Квадрат разности всегда больше, либо равен нулю. Функция распределения подсистемы всегда неотрицательно по самому ее определению. Поэтому подынтегральная функция в данном интеграле больше, либо равна нулю во всей области интегрирования. Следовательно, этот интеграл будет стремиться к нулю только тогда, когда квадрат отклонения нашей величины от среднего сам стремится к нулю. Другими словами, среднее значение квадрата отклонения от среднего будет мало только тогда, когда вероятность значительных отклонений нашей величины от своего среднего будет мала. Величина называется средней квадратичной флуктуацией величины . Эта величина как раз характеризует в среднем ширину интервала отклонения величины от ее среднего значения.

Теперь получим одно полезное выражение для средней квадратичной флуктуации. Для этого в определении этой величины давайте раскроем квадрат разности. В результате получим

. (13)

Далее воспользуемся тем, что среднее суммы равно сумме средних. Таким образом, имеем

. (14)

Теперь воспользуемся тем, что константу можно выносить за знак усреднения. Вынося в третьем слагаемом константу , получаем

. (15)

Сокращая одинаковые слагаемые, окончательно имеем

. (16)

Таким образом, среднеквадратичная флуктуация определяется разностью среднего квадрата и квадрата среднего.

Отношение называют относительной флуктуацией величины . Чем она меньше, тем меньшую часть времени система будет проводить в микросостояниях, в которых отклонение величины от своего среднего значения будет составлять значительную часть последнего.

Покажем теперь, что относительная флуктуация быстро уменьшается с увеличением размеров тела (т.е. с увеличением в нем числа частиц). Для этого предварительно заметим, что большинство величин, представляющих физический интерес являются аддитивными . Это обстоятельство есть следствие того факта, что энергия взаимодействия подсистемы со своим окружением много меньше ее внутренней энергии, и состоит в том, что значение такой величины для всего тела есть сумма значений этой величины для отдельных его макроскопических частей.

Пусть есть такая аддитивная величина. Разобьем тело на большое число примерно одинаковых макроскопических частей. Тогда в силу аддитивности среднее значение нашей величины для всей системы равно сумме средних значений этой величины для частей, на которые мы разбили нашу систему

. (17)

Если мы теперь будем увеличивать размер тела, сохранив размер частей, т.е. будем “прикреплять” к нашему телу дополнительные части, то у нас будет расти . Из (17) ясно, что при увеличении размеров тела среднее системы будет расти примерно пропорционально .

Далее определим среднюю квадратичную флуктуацию. Имеем

. (18)

Отсюда в силу статистической независимости частей

. (19)

Поскольку для любой подсистемы, то вторая сумма равна нулю, и мы имеем

. (20)

Из последней формулы видно, что с ростом среднее квадрата отклонения аддитивной величины, характеризующей все тело, увеличивается приблизительно пропорционально , а средне квадратичная флуктуация увеличивается приблизительно пропорционально . Следовательно, среднеквадратичная флуктуация с ростом будет уменьшаться обратно пропорционально , т.е.

. (44)

Когда мы увеличиваем размер тела, сохраняя размер частей, т.е. когда мы добавляем к телу дополнительные части, то число N этих частей, очевидно, будет увеличиваться приблизительно пропорционально числу частиц в теле. Таким образом, можно утверждать, что относительная флуктуация всякой аддитивной величины уменьшается обратно пропорционально квадратному корню из числа частиц в системе. Поскольку в макроскопических телах число частиц колоссально, то относительная флуктуация любой аддитивной величины (а именно такие величины в большинстве случаев представляют физический интерес) будет чрезвычайно мала. Поэтому саму величину можно с большой точностью считать постоянной во времени и равной своему среднему значению.

Лекция 2. Зависимость функции распределения от макроскопического состояния

окружающей среды. Внешние параметры. Теплообмен..

Теперь обсудим то, каким образом информация об окружающей среде входит в функцию распределения макроскопической системы, которая находящейся в равновесии с этой средой. Как обсуждалось на прошлой лекции, при описании макроскопического тела, находящегося в равновесии с окружающей средой, истинные значения всех его макроскопических характеристик можно с огромной точностью заменить на средние значения, которые получаются с помощью функции распределения, определенной таким образом, что она не зависит от микросостояния окружающей среды. Однако то обстоятельство, что функция распределения равновесной системы не зависит от микросостояния окружающей среды вовсе не означает, что эта функция вообще не содержит информацию об окружающей среде. Информация об окружающей среде в функции распределения, конечно же, присутствует. Однако присутствует она в виде параметрической зависимости от макроскопического состояния окружающей среды. Другими словами, функция распределения равновесной системы параметрически зависит от макроскопического состояния окружающей среды и не зависит от того, с помощью какого микросостояния это макросостояние окружающей среды реализуется. На языке термодинамики это означает, что информация о влиянии окружающей среды входит в функцию распределения изучаемого тела через параметрическую зависимость этой функции от внешних термодинамических параметров и температуры, которые задают состояние термодинамического равновесия, в котором находится наше тело. В данном состоянии термодинамического равновесия, т.е. при данных конкретных значениях внешних термодинамических параметров и температуры, явный вид функции распределения нашей системы вполне определенный. Однако если теперь поместить наше тело в другое состояние термодинамического равновесия, которое определяется другими значениями внешних термодинамических параметров или температуры, то явных вид функции распределения нашей системы изменится. Однако при этом в обоих состояния термодинамического равновесия, функция распределения нашей системы не будет зависеть от микросостояния окружающей среды. Конечно, если мы учтем влияние микроскопического состояния окружающей среды на распределение вероятности различных микросостояний нашего тела, то мы построим формально более точную теорию. Однако для нашей задачи практическая значимость этого уточнения будет фактически нулевой.

Давайте теперь разбираться, что такое внешние и внутренние термодинамические параметры, и какова их роль в статистической теории

Прежде всего, еще раз подчеркну, что мы различаем два понятия состояния макроскопической системы. Одно - это микроскопическое состояние. Другое - это состояние термодинамического равновесия, т.е. состояние макроскопическое. Задать микроскопическое состояние системы - значит указать все ее координаты и импульсы системы. Такой способ описания состояния системы является максимально подробным. Однако, как мы уже обсуждали, для практических приложений столь подробное описание состояния макроскопической системы является излишним. Дело в том, что, как правило, на практике мы имеем дело с макроскопическими параметрами, т.е. с измеряемыми с помощью макроскопических приборов величинами, такими как объем, давление, температура, плотность, концентрация, упругость, намагниченность, поляризация и т.п. Поэтому на практике состояние макроскопических тел, как правило, характеризуется этими макроскопическими параметрами. Охарактеризованное таким способом состояние макроскопической системы называется макроскопическим состоянием.

По самому своему смыслу макроскопические параметры огрублено (усреднено) характеризуют макроскопическую систему.

Рассмотрим простейший пример – сосуд с разреженным газом, помещенный в термостат. Состояние термодинамического равновесия этого газа задается двумя макроскопическими параметрами: внешним термодинамическим параметром – объемом сосуда и температурой термостата.

Понятно, что точная микроскопическая картина взаимодействия частиц газа с атомами стенки сосуда является необычайно сложной. Для строго описания такой картины нужно учесть структуру вещества стенки, тепловые колебания атомов стенки, квантовомеханические особенности взаимодействия частиц газа с атомами стенки, причем мы должны учесть именно взаимодействие, т.е. взаимное влияние атомов стенки и частиц газа на состояние друг друга, ну и т.д.

Однако для практических приложений столь подробно описывать влияние стенки на газ нет никакой необходимости. Достаточно поступить следующим образом. Всю сложную структуру стенки сосуда можно с огромной точностью заменить жесткой неизменной во времени математической поверхностью, непроницаемой для молекул газа. Внешний параметр – объем газа является функцией координат точек этой поверхности, которая имитирует внешнее по отношению к нашему газу тело – стенку сосуда. Причем эта поверхность и, соответственно, объем никак не зависит от координат и импульсов молекул газа. С точки зрения математического аппарата статистической теории, проводя такое огрубление стенки сосуда, мы очень сложное взаимодействие газа и стенки приближенно учитываем, рассматривая наш газ во внешнем потенциале следующего вида

. (1)

Другими словами, мы влияние стенки на аппроксимируем внешним по отношению к нашу газу силовым полем с данным потенциалом. Таким образом, мы нашему разреженному газу приписываем эффективную функцию Гамильтона

, (2)

которая есть кинетическая энергия газа плюс потенциальная энергия газа во внешнем силовом поле, которое моделирует влияние стенки сосуда на газ. Это внешнее силовое поле определяется внешним параметром – объемом. Поэтому эффективный гамильтониан нашего газа параметрически зависит от объема.

Обращаю ваше внимание, что независимыми переменными в этом гамильтониане являются координаты и импульсы только нашего газа. Однако, включив в этот Гамильтониан второе слагаемое, мы учли все существенное влияние на наш газ окружающей среды, которое можно с большой точностью аппроксимировать чисто силовым внешним воздействием. Это внешнее силовое поле определяется внешним параметром – объемом. Поэтому эффективный гамильтониан нашего газа параметрически зависит от объема.

Однако при описании нашего газа помимо влияния стенки сосуда мы еще обязательно должны учесть теплообмен между газом и термостатом. При этом нужно иметь ввиду, что теплообмен между системой и окружающей средой принципиально нельзя свести к внешнему силовому воздействию на изучаемую систему. Другими словами, влияние теплообмена на газ принципиально нельзя учесть, рассмотрев наш газ в неком внешнем силовом поле.

Вообще, любое действие есть аппроксимация некого взаимодействия. Если говорить строго, то в природе не бывает действия, бывает только взаимодействие. Другими словами, любые две системы влияют на состояние друг друга самосогласованным образом. Когда мы говорим о внешнем поле, приложенном к изучаемой системе, то это всегда приближение.

В качестве примера рассмотрим свободное падение тела в поле тяготения Земли. Строго говоря, тело и Землей взаимодействуют. Поэтому состояние тела и состояние Земли меняются самосогласованным образом. Однако масса тела ничтожна по сравнению с массой Земли. Поэтому влиянием состояния маркера на состояние Земли можно пренебречь, и считать, что движение маркера происходит во внешнем силовом поле – поле тяжести .

Теперь, опираясь на данный пример, поймем суть того, как в статистической теории и, соответственно, в термодинамике учитывается теплообмен между изучаемой макроскопической системой и окружающей средой.

Прежде всего, вспомним, что согласно постановке задачи наш газ и термостат вместе образует замкнутую систему. При этом наша система очень мала по сравнению с термостатом, так что влияние нашей системы на термодинамическое состояние термостата пренебрежимо мало.

Для краткости всю совокупность координат нашего газа обозначим . Всю совокупность импульсов газа обозначим . Соответственно, координаты и импульсы термостата обозначим и . Функцию Гамильтона всей замкнутой системы “наш газ+термостат” обозначим . Она, очевидно, зависит как от координат и импульсов нашего газа, так и от координат и импульсов термостата.

По определению энергия замкнутой системы не меняется. Функция Гамильтона системы есть ее полная энергия, рассмотренная как функция ее координат и импульсов. Следовательно, функция Гамильтона всей замкнутой системы “наш газ+термостат” равна некоторой константе Е. Ясно, что энергия Е задает состояние равновесия всей системы “наш газ+термостат”.

При попытке учесть взаимодействие нашего газа с термостатом, используя методы обычной механики, мы сталкиваемся с еще большей проблемой. Мало того, что наша система имеет огромное число степеней свободы, так вообще мы обязаны применять аппарат обычной механики ко всей замкнутой системе , состоящей из нашей системы и окружающей среды.

Действительно, функция Гамильтона совокупности “наша система+термостат”, вообще говоря, содержит три члена - функцию Гамильтона нашей системы , функцию Гамильтона термостата , и член , который описывает неучтенное ранее взаимодействие нашей системы с окружающей средой.

.(3)

Причем третий член описывает именно взаимодействие. Его нельзя представить в виде суммы двух функций, одна из которых зависит от микросостояния только нашей системы, а другая – от микросостояния только окружающей среды. Уравнения Гамильтона в этом случае имеют вид

, (4)

, (5)

, (6)

. (7)

Индекс пробегает значения , где - число степеней свободы нашей системы. Соответственно, индекс пробегает значения , где - число степеней свободы термостата.

Из-за наличия третьего члена мы не можем систему уравнений для системы представить в виде совокупности двух независимых систем уравнений, в одну из которых входят координаты и импульсы только нашей системы, а в другую – координаты и импульсы только окружающей среды. Таким образом, когда мы хотим учесть взаимодействие нашей системы с окружающей средой мы тем более должны пользоваться статистическим подходом.

Точный вид члена необычайно сложный. Однако поскольку наш газ находится в равновесии с термостатом, то отсутствуют макроскопический поток энергии между нашей системой и окружающей ее средой. Если мы возьмем любую макроскопическую часть границы между газом и термостатом, вычислим поток энергии через эту поверхность, и затем усредним его по времени существенно превышающем времена микроскопических процессов, то мы с огромной точностью получим нуль. Следовательно, подавляющую часть времени наш газ будет находится в микросостояниях с энергией близкой к ее статистическому среднему (внутренней энергии). Если говорить на языке функции распределения, то в наиболее вероятных микросостояниях энергия нашего газа будет близка к его внутренней энергии. Поскольку, как мы видели, внутренняя энергия макроскопических систем существенно превышает их внутреннюю энергию, то в наиболее вероятных микросостояниях энергия нашего газа, и тем более, термостата будет существенно превышать , и в выражении (3) мы можем предречь третьим членом, аппроксимируя функцию Гамильтона замкнутой системы “наш газ+термостат” суммой Гамильтонианов нашего газа и термостата

. (8)

Однако при такой аппроксимации мы вовсе не исключаем из нашей задачи возможность обмена энергией между нашим газом и термостатом. Мы просто пользуемся тем обстоятельством, что энергия взаимодействия хотя и отлична от нуля, но настолько мала, что при вычислении энегии всей системы ею можно пренебречь на фоне больших значений энергий газа и термостата. Когда мы задаем состояние равновесия замкнутой системы “наш газ+термостат”, то мы фиксируем энергию всей этой замкнутой системы . Она у нас равна Е. Однако при этом мы не фиксируем энергию газа и термостата по отдельности. Энергия газа и энергия термостата могут принимать различные значения, просто эти значения должны быть такими, чтобы их сумма равнялась заданной константе Е. Например, когда энергия газа уменьшается на некоторую величину энергия термостата должна на эту же величину увеличится. Тогда сумма энергий газа и термостата не изменится. Таким образом, несмотря на то, что мы в этой аппроксимации гамильтониана выбросили член, описывающий именно взаимодействие, мы, тем не менее, сохраняем возможность теплообмена между нашей системой и окружающей средой. Выбросив член мы просто исключаем из рассмотрения микроскопический механизм теплообмена, тем самым переходя к термодинамической его трактовке.

Указанная аппроксимация гамильтониана является одним из основных моментов, используемых при решении задачи о функции распределения нашего газа. В дальнейшем мы непосредственно увидим, что функция распределения нашего газа имеет следующий вид

(9)

Здесь - постоянная Больцмана, Т – термодинамическая температура термостата. С есть нормировочная постоянная.

Заметим, что эта температура определяется, строго говоря, равновесным состоянием всей замкнутой системы, а именно – ее энергией Е. Но поскольку наш газ представляет собой очень малую по сравнению с термостататом систему, то энергия Е определяется главным образом энергией термостата. Следовательно, и температура Т определяется главным образом термостатом. Именно это имеют ввиду, когда говорят “температура термостата”.

Глядя на выписанную формулу для функции распределения нашего газа, легко видеть, что различные значения энергии нашей системы могут реализовываться с различной вероятностью, которая определяется температурой Т.

Для того, чтобы сказанное было еще нагляднее, найдем вероятность того, что энергия нашего газа лежит в элементарном интервале от до .

Рассмотрим в фазовом пространстве нашего газа две поверхности постоянной энергии. Одна изоэнергетическая поверхность определяется уравнением , другая - . При этом мы будем считать две эти поверхности очень-очень близкими, т.е будем считать, что .

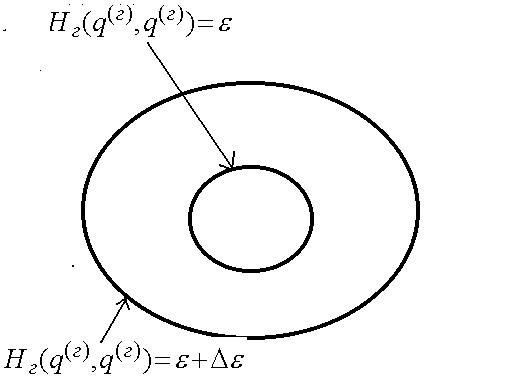
Рис.1

Давайте найдем объем фазового пространства между этими двумя изоэнергетическими поверхностями.

Обозначим

(10)

объем фазового пространства, ограниченный изоэнергетической поверхностью . Тогда - объем фазового пространства, ограниченный изоэнергетической поверхностью . Объем фазового пространства между двумя этими изоэнергетическими поверхностями

. (11)

У нас . Малым параметром всегда нужно пользоваться. По малому параметру всегда нужно разлагаться в ряд. Поэтому, естественно, мы должны разложить в ряд Тейлора в окрестности точки . Имея в виду то, что в дальнейшем мы будем от близких изоэнергетических поверхностей переходить к бесконечно близким, ограничимся в этом разложении только членом, линейным по .

Таким образом, мы пишем

. (12)

Сокращая одинаковые члены, получаем

. (13)

Если мы теперь устремим к нулю, то мы получим, что объем фазового пространства между двумя изоэнергетическими поверхностями и , дается выражением

. (14)

Теперь мы можем написать одну очень полезную на практике формулу. Пусть есть явная функция энергии газа. Она является неявной функции координат и импульсов нашего газа. Координаты и импульсы входят в эту функцию только в виде определенной комбинации, которая представляет собой функцию Гамильтона нашего газа. Тогда

, (15)

где

. (16)

Давайте теперь функцию распределения нашего газа проинтегрируем по его объему между изоэнергетическим поверхностями и .

. (17)

Этот интеграл есть вероятность того, что энергия нашего газа лежит в интервале от до .

Действительно. Рассмотрим в качестве элементарного событие, состоящее в том, что наш газ находится в конкретном элементарном объеме своего фазового пространства. Два различных таких события, понятно, не могут произойти одновременно. События, которые не могут произойти одновременно, в теории вероятности называются несовместными.

В теории вероятности имеется так называемая теорема о сложении вероятности. Смысл этой теоремы состоит в следующем. Пусть у нас имеются два несовместных события. Обозначим одно событие цифрой 1, его вероятность обозначим . Другое событие обозначим цифрой 2, его вероятность обозначим . Тогда вероятность того, что произойдет какое-то из этих событий – или событие 1, или событие 2

. (18)

Возвращаемся к нашему газу. Рассмотрим два элементарных события. Первое событие состоит в том, что наш газ находится в элементарном объеме его фазового пространства, окружающем точку . Второе событие состоит в том, что наш газ находится в другом элементарном объеме его фазового пространства, окружающем другую точку . Поскольку эти события являются несовместными, то согласно теореме сложения вероятностей вероятность того, что наш газ будет находится в каком-то из этих элементарных объемов есть

. (19)

Интеграл есть аналог суммы в ситуации, когда суммируемые величины меняются непрерывно. Таким образом, если мы проинтегрируем функцию распределения нашего газа между двумя этими изоэнергетическими поверхностями, то мы получим вероятность того, что наш газ находится в какой-то из точек, лежащей между этими поверхностями постоянной энергии. Но в любой из этих точек фазового пространства энергия газа лежит в интервале от до . Следовательно, этот интеграл есть вероятность того, что энергия нашего газа лежит в этом интервале.

Подставим явный вид функции распределения и воспользуемся соотношением (15). В результате получим

. (20)

Отсюда вероятность того, что энергия нашего газа лежит в интервале от до есть

. (21)

Теперь уже совмем четко видно, что наш гах может иметь не одну определенную энергию, а с определенной вероятностью ряд значений энергии. Причем распределение вероятностей различных значений энергии определяется температурой термостата.

Вернемся теперь к выражению для функции распределения нашего газа. Из этого выражения видно, что функция распределения нашего газа зависит только от его координат и импульсов, и не зависит от микросостояния окружающей среды. Информация об окружающей среде входит в эту функцию распределения нашего газа через параметрическую зависимость от внешнего параметра - объема и от температуры термостата, которые задают его конкретное состояние термодинамического равновесия. В данном состоянии термодинамического равновесия, т.е. при заданном значении объема и температуры, явный вид функции распределения нашей системы вполне определенный. Однако, если теперь поместить нашу систему в другое состояние термодинамического равновесия, которое определяется другими значениями объема или температуры, то явных вид функции распределения нашей системы изменится. Однако при этом в обоих состояния термодинамического равновесия, функция распределения нашего газа не зависит от микросостояния окружающей среды.

Далее среднее значение любой функции координат и импульсов нашего газа, т.е. равновесное значение соответствующего внутреннего параметра, есть

. (22)

Из этого выражения видно, что любой внутренний параметр нашего газа есть функция двух независимых переменных: внутреннего параметра – объема газа и температуры термостата.

Отсюда как раз и следует, что состояние равновесия нашего газа задается двумя термодинамическими параметрами – объемом и температурой.

Теперь те основные моменты, с которыми мы разобрались на данном конкретном примере, сформулируем для общего случая.

Прежде всего, еще раз подчеркнем, что в дальнейшем мы всегда будем иметь дело с макроскопическими системами, находящимися в равновесии с окружающей средой. Когда мы будем говорить о термодинамических процессах, то мы всегда будем рассматривать квазистатические обратимые процессы. Напомню, что процесс называется квазистатическим, если внешние условия изменяются настолько медленно, что в любой момент времени систему можно описать так, как если бы она находилась в состоянии термодинамического равновесия. Другими словами, квазистатический процесс можно себе представить как непрерывно разворачивающуюся во времени цепочку равновесных состояний. Процесс называется обратимым, если при изменении внешних условий в обратном порядке система проходит в обратном порядке те же состояния, что и при прямом процессе.

Состояние термодинамического равновесия описывается с помощью ряда внешних и внутренних макроскопических параметров. Для характеристики состояния системы необходимо задать еще и температуру. Разделение параметров на внешние и внутренние осуществляется следующим образом. Часть влияния окружающей среды на изучаемое тело можно аппроксимировать чисто силовым внешним воздействием, рассмотрев нашу подсистему во внешних силовых полях. Внешние параметры нашей подсистемы представляют собой величины, которые определяют эти внешние силовые поля. Внешние параметры есть функции координат идеализированных источников этих внешних силовых полей. Подчеркну, что по самому своему смыслу внешние параметры не зависят от координат и импульсов самой изучаемой системы. Под внутренними параметрами системы понимают средние значения любых функций координат и импульсов самой этой системы.

В только, что рассмотренном примере сосуда с газом, объем, надеюсь всем понятно, является внешним параметром. В качестве примера внутреннего параметра можно привести давление газа на стенку сосуда. Давление по самому своему определению есть среднее значение функции координат и импульсов частиц газа. Поэтому давление для нашей системы будет внутренним параметром.

В качестве другого примера можно привести тот же газ, помещенный в поле тяжести. В этом случае у нас появляется еще один внешний параметр – сила тяжести. Сила тяжести является внешним параметром, поскольку она зависит от положения внешних источников тяготения и не зависит от микросостояния самого газа.

В качестве еще одного примера можно привести опять тот же газ, помещенный в стационарное электрическое поле. Напряженность поля является внешним параметром, поскольку она определяется положением внешних зарядов, вызывающих это поле. Поляризация же газа есть внутренний параметр, поскольку она определяется положением зарядов в непосредственно в молекулах самого газа.

Для того, чтобы не было путаницы в дальнейшем, подчеркну, что температуру мы не будем относить ни к внешним, ни к внутренним параметрам. Она у нас будет стоять особняком.

Также отмечу, что в термодинамическом равновесии все внутренние параметры системы являются функцией внешних параметров и температуры. Другими словами, макроскопическое состояние системы, находящейся в равновесии со своим окружением, задается внешними параметрами и температурой.

Договоримся о следующих обозначениях, которые будем везде в дальнейшем использовать Совокупность координат и импульсов изучаемой нами системы мы будем обозначать и . Совокупность координат и импульсов окружающей среды будем обозначать и . Совокупность всех внешних параметров, задающих состояние равновесия нашей системы, будем обозначать буквой . Один- i-ый - внешний параметр будем обозначать (буквой с индексом i).

При рассмотрении системы, находящейся в равновесии с окружающей средой, мы очень-очень сложную точную функцию Гамильтона замкнутой системы, состоящей из изучаемого тела и окружающей среды, заменяем на приближенную, которую представляем в виде суммы эффективной функции Гамильтона нашей системы и эффективной функции Гамильтона окружающей среды. Т.е. мы пишем, что

. (23)

Влияние окружающей среды которое можно с достаточной точностью аппроксимировать чисто силовым внешним воздействием на изучаемое тело, мы учитываем в эффективной функций Гамильтона нашей системы . Когда мы пишем функцию Гамильтона нашей системы, то мы идеализируем окружающую среду, представляя ее в виде совокупности источников классических силовых полей, на которые наша система не оказывает никакого воздействия. Другими словами, при написании гамильтониана нашей системы, мы всю окружающую среду заменяем внешними силовыми полями. Эти внешние силовые поля определяются внешними параметрами. Поэтому эффективная функция Гамильтона нашей системы параметрически зависит от внешних параметров.

Теплообмен между нашей системой и окружающей средой мы учитываем следующим образом. Мы фиксируем функцию Гамильтона всей замкнутой системы, но при этом мы не фиксируем по отдельности гамильтониан нашей системы и гамильтониан окружающей среды . Этим мы оставляем возможность теплообмена между нашей системой и окружающей средой. В результате мы получаем, что различные значения энергии нашей системы могут реализовываться с различной вероятностью, которая определяется температурой.

Для системы, находящейся в состоянии равновесия, т.е. при заданных конкретных значениях внешних параметров и температуры, независимыми переменными в функции распределения являются координаты и импульсы только этой системы. Информация об окружающей среде входит в функцию распределения нашей системы через параметрическую зависимость от внешних параметров и температуры. Вводя такую функцию распределения, мы на самом деле при определении вероятности различных микроскопических состояний нашей системы учитываем влияние только макроскопического состояния окружающей среды, которое в данном равновесном состоянии фиксировано, и считаем, что эти вероятности никак не зависят от того, каким микросостоянием окружающей среды реализуется заданное ее макроскопическое состояние.

Лекция 3. Микроканоническое и каноническое распределения Гиббса в классической статистической теории

Изолированная система. Микроканоническое распределение

Рассмотрим ситуацию, когда изучаемая система является адиабатически изолированной от окружающей среды или, иначе, замкнутой. В этом случае изучаемая система отделена от окружающей среды адиабатическими стенками, которые препятствуют как обмену частицами, так и теплообмену между системой и окружающей средой. При этом принципиально, что стенки препятствуют именно взаимодействию. Эта постановка задачи вовсе не исключает наличие влияния окружающей среды, которое может быть с большой степенью точности аппроксимировано чисто силовым внешним воздействием. Другими словами, под замкнутой мы понимаем систему, все существенное влияние на которую можно с достаточной точностью учесть, рассмотрев ее во внешних стационарных силовых полях. Главное, что замкнутая система не обменивается с окружающей средой ни частицами, ни энергией. При таком задании нашей системы мы фиксируем число частиц в ней , ее объем и остальные внешние параметры , а также ее энергию. Причем речь идет не о внутренней энергии, а именно об энергии в обычном механическом понимании. Состояние равновесия такой системы задается внешними параметрами и ее энергией. Для полноты информации – для того, чтобы написать функцию Гамильтона нашей системы - нам еще, конечно же, нужно знать число частиц N в нашей системе. Распределение вероятности различных микросостояний замкнутой системы называется микроканоническим.

Задача о функции распределения изолированной системы является исходной для статистической теории. Вид функции распределения для замкнутой системы являются отправной точкой при нахождении канонического и большого канонического распределения.

Вид функции распределения для адиабатически изолированной системы непосредственно вытекает из постулата, который носит название принципа равной вероятности. Этот принцип состоит в следующем. Состояние равновесия нашей замкнутой системы задается ее энергией Е. Функция Гамильтона системы есть ни что иное, как ее полная энергия. Следовательно, микросостояния нашей системы, возможные в заданном состоянии равновесия, определяются условием

. (1)

Никакие другие микросостояния нашей системы в этом ее состоянии равновесия не возможны. Утверждение постулата равной вероятности состоит в том, что с равной вероятностью реализуется любое микросостояние, возможное в данном состоянии равновесия изолированной системы.

Непосредственно из постулата равной вероятности следует, что функция распределения нашей замкнутой системы имеет вид

. (2)

Действительно, пусть энергия нашей системе является не строго постоянной, а может меняться в очень малом интервале от до . Тогда возможные микросостояния нашей системы определяются условием

. (3)

Пусть ширина интервала энергии хоть и конечна, но настолько мала, что для нашей системы с большой точностью справедлив принцип равной вероятности. Т.е. ширина интервала настолько мала, что каждое микросостояние, энергия которого попадает в данный интервал, реализуется с равной вероятностью. Другими словами, функция распределения нашей системы имеет вид

, (4)

где С – константа.

Равновесное значение макроскопического параметра, как мы значем, есть

. (5)

Теперь для того, чтобы перейти от квазизамкнутой системы к истинно замкнутой, мы должны устремить к нулю. В результате мы получим наш внутренний макроскопический параметр

. Согласно определению дельта-функции Дирака этот предел равен

. (6)

Таким образом, функцию распределения адиабатически изолированной системы мы можем написать как произведение нормировочной постоянной на дельта-функцию Дирака, аргумент которой есть разность функции Гамильтона нашей системы и энергии E

.

Значение постоянной определяется условием нормировки

. (7)

Подставляем в условие нормировки явный вид функции распределения и переходим от интегрирования по фазовому пространству к интерированию по энергии в соответствии с той теоремой, которую сформулированной на прошлой лекции. В результате получим

, (8)

где

, (9

(10)

объем фазового пространства, ограниченный поверхностью постоянной энергии .

Воспользовавшись основным свойством дельта-функции

. (11)

В результате получаем

. (12)

Отсюда постоянная есть

. (13)